基于Matlab／Simulink的空空导弹攻击区仿真＊

曲晓燕，张 林，范 庚

（1海军航空工程学院，山东烟台 264001；2空军驻西北地区军事代表室，西安 710043）

0 引言

空空导弹攻击区是空空导弹作战效能的综合体现，是分析导弹性能、指导作战运用的重要技术依据[1－2]。由于导弹的价格昂贵以及攻击条件的复杂多样，用大量靶场试验的方法得出各种攻击条件下的攻击区是不现实的。通过建立数学模型，利用计算机仿真计算导弹的攻击区，可以在理论上得出攻击区的范围和变化规律，从而为进一步发挥导弹的作战效能和火控系统软件设计提供参考数据[3]。

空空导弹攻击区的计算多采用工程计算语言编写，例如C、C＋＋等。但这些语言存在仿真过程可视化效果差、编程复杂、计算时间长等不足。针对这些问题，文中提出了一种简便有效的仿真计算方法：在Matlab 6.5环境下，利用Simulink建立了弹道仿真模型，并通过建立脚本文件，运用Matlab编程调用该模型，对空空导弹攻击区进行了仿真计算。

1 坐标系选取及其转换

1.1 惯性坐标系

惯性坐标系是一个固定坐标系，坐标系原点OI取在导弹发射原点；YI轴取初始目标线，方向由导弹指向目标；ZI轴取垂直YI轴向下；XI轴垂直YI轴和ZI轴，方向符合右手定则。

1.2 弹体坐标系

弹体坐标系与导弹固联在一起，坐标原点取导弹重心OM；X轴取导弹纵轴，方向指向导弹头部；Y轴取导弹的俯仰轴，方向垂直X轴向下；Z轴垂直X轴和Y轴，方向符合右手定则。

1.3 坐标系转换

不考虑横滚角的影响，惯性坐标系到弹体坐标系可先绕ZI轴转过偏航角ψm，再绕YI轴转过俯仰角γm求得。转换阵表示为[4]：

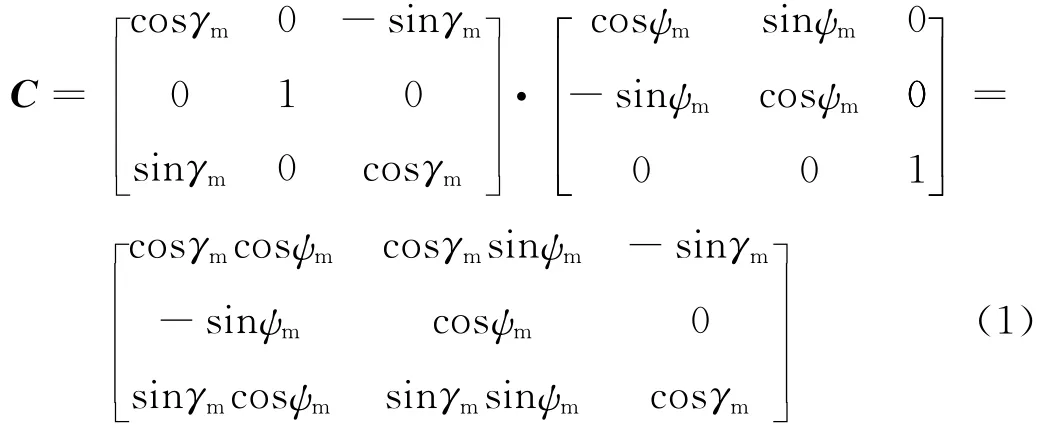
2 弹道仿真模块化设计

文中采用Simulink工具箱建立弹道仿真模型。根据各部分的任务及功能，将系统分为4个模块：目标运动模块、导弹运动模块、相对运动模块、导弹制导与控制模块和命中条件限制模块，各模块的输入输出信号如图1所示。

在Simulink提供的图形用户界面GUI上，只要进行鼠标的简单拖拉操作就可构造出复杂的仿真模型。Simulink的分层结构，从建模角度讲，既适于自上而下（top－down）的设计流程（概念、功能、系统、子系统、直至器件），又适于自下而上（bottom－up）逆程设计；从分析研究角度讲，这种Simulink模型不仅能让用户知道具体环节的动态细节，而且能让用户清晰的了解各器件、各子系统、各系统间的信息交换，掌握各部分之间的交互影响[5]。

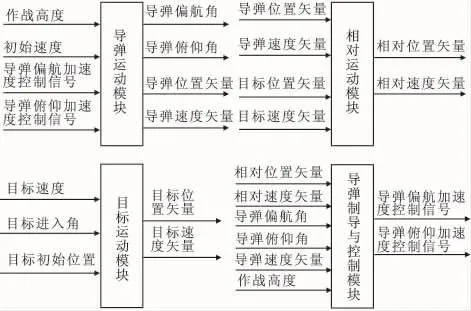
图1 模块输入输出信号图

2.1 目标运动模块

假定目标和导弹的初始位置在同一水平面上，导弹在惯性坐标系的原点，目标坐标为（0，Yt0，0），目标初始速度和YI轴的夹角为ηt0，即目标进入角。两者的初始相对位置如图2所示。

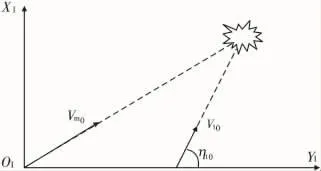
图2 导弹 －目标初始相对位置示意图

惯性坐标系下的目标匀速直线运动方程如式（2）所示。

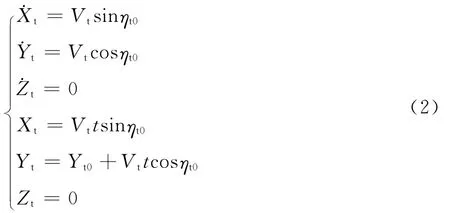
利用Simulink的不同功能块设计目标匀速直线运动运动模块如图3所示。

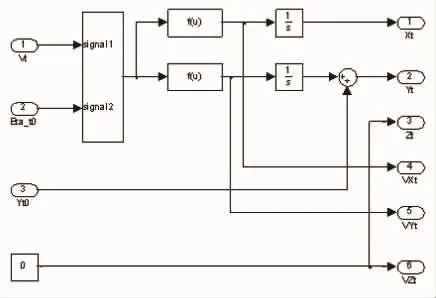
图3 目标匀速直线运动模块Simulink实现框图

2.2 导弹运动模块

由于三自由度模拟非常接近六自由度模拟计算结果，且计算速度远高于六自由度模拟，因此通常采用三自由度模拟计算结果作为理论攻击区[6]。文中导弹数学模型采用三自由度模型，但考虑了导弹控制系统的时间延迟。导弹数学模型如图4所示。导弹运动模块设计如图5所示。

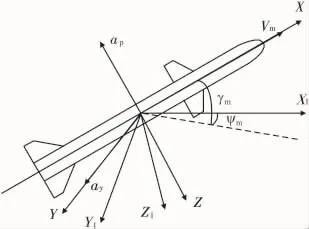
图4 导弹数学模型

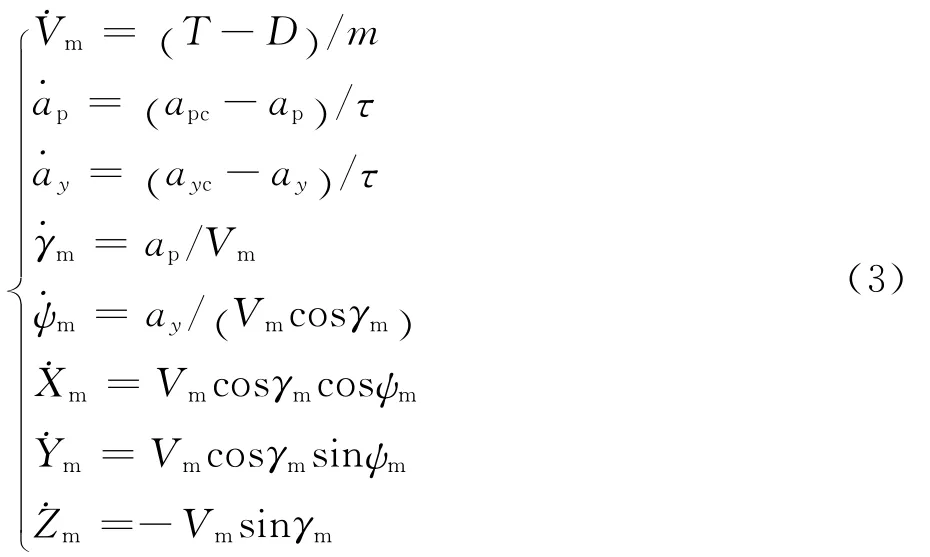
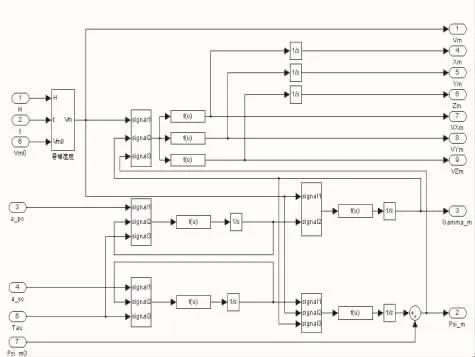
图5 导弹运动模块Simulink实现框图

2.3 相对运动模块

设（Xt，Yt，Zt）、（Xm，Ym，Zm）分别是目标和导弹在惯性坐标系下任意时刻的坐标，则导弹与目标相对运动方程如式（4）。相对运动模块设计如图6所示。

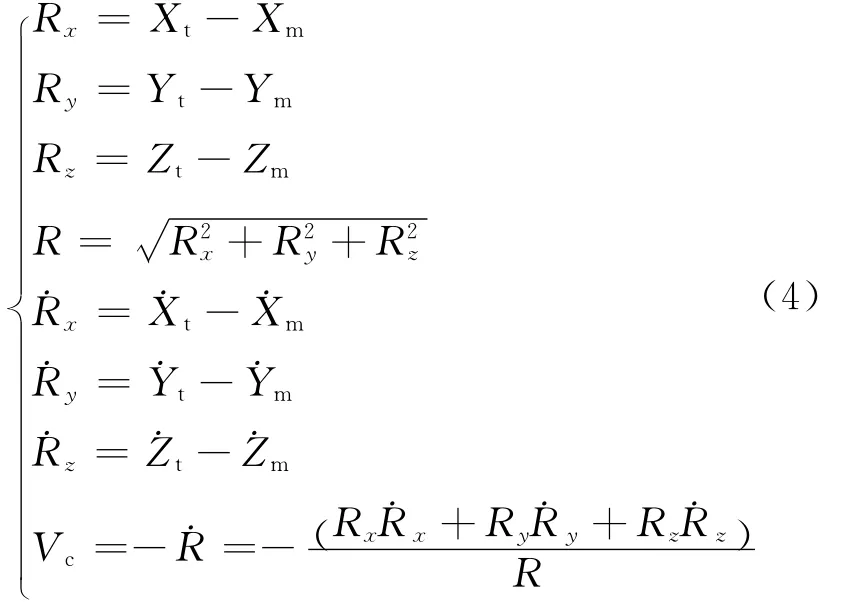
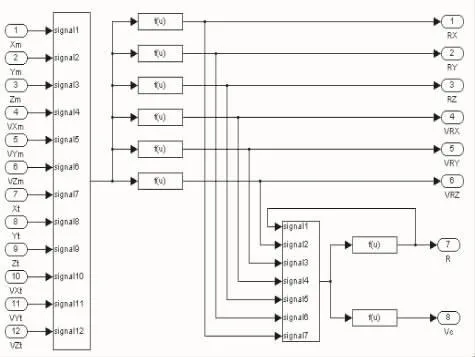
图6 相对运动模块Simulink实现框图

2.4 导弹制导与控制模块

假设导弹采用广义的比例导引律，导弹俯仰和偏航两方向上的控制方程如下[4]：

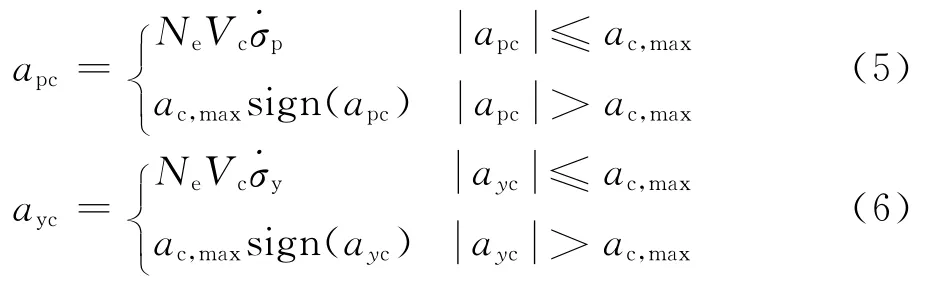
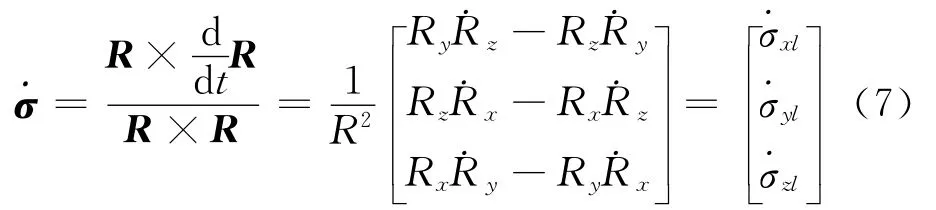
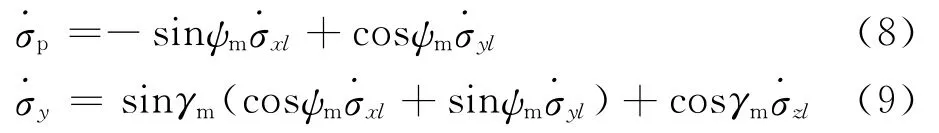
导弹制导与控制模块设计如图7所示。

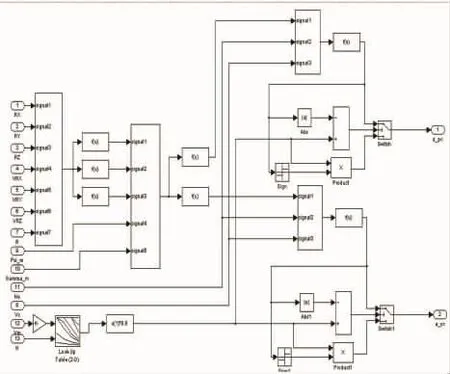
图7 导弹制导与控制模块Simulink实现框图

2.5 命中条件限制模块

导弹能否命中目标受到很多因素的限制[7]。文中主要考虑以下参数限制：

1）导弹飞行时间小于导弹工作时间（t＜Tmax）；

2）弹目相对速度大于最小限制值（Vc＞Vc，min）；

3）导弹飞行时间大于导弹安全飞行时间（t＞Tsafe）；

4）脱靶量小于或者等于导弹杀伤半径（R≤Rmax）。

命中条件限制模块设计如图8所示。

3 攻击区仿真程序实现

在设计攻击区仿真程序时，首先建立脚本文件，利用Matlab语言编程设置仿真参数、改变目标进入角，并采用二分法计算初始目标距离；解算弹道时，在脚本文件中调用Simulink建立的弹道模型。仿真程序流程及相应程序如图9所示（图中程序部分以计算导弹最大发射距离为例）。

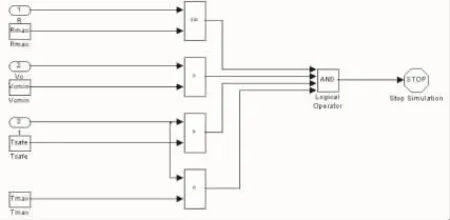
图8 命中条件限制模块Simulink实现框图

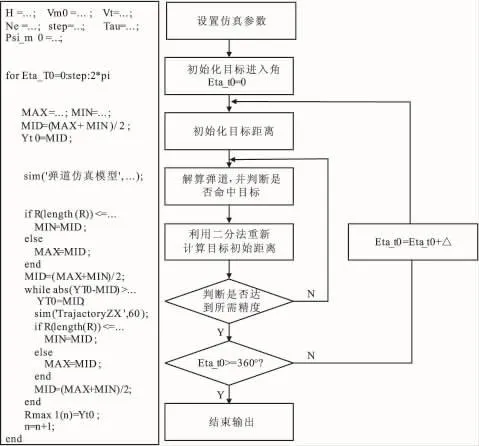
图9 仿真程序流程及相应程序

4 仿真结果

利用上述程序在计算机上进行了仿真计算。以下给出了不同作战条件和不同目标机动方式下的导弹攻击区。

初始条件：作战高度H＝5000m，载机速度Vm＝300m／s，目标速度Vt＝300m／s，目标作匀速直线运动。仿真结果如图10所示。

初始条件：作战高度H＝10000m，载机速度Vm＝200m／s，目标速度Vt＝300m／s，目标作匀速直线运动。仿真结果如图11所示。

5 结束语

文中针对空空导弹攻击区计算过程的特点，采用Simulink方块图与Matlab语言编程相结合的方法对

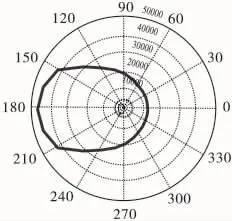
图10 仿真结果

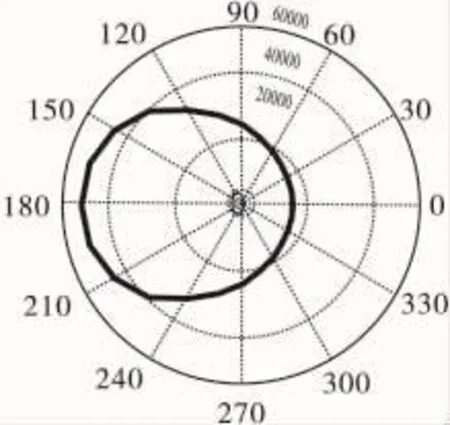
图11 仿真结果

攻击区进行了仿真，为空空导弹攻击区的仿真计算提供了一种简便有效的方法。该方法具有以下特点：

a）可视化效果好。Matlab包含丰富的绘图函数，而且采用Simulink建立弹道仿真模型，能够对多个输出进行同时监控，因而用户可以方便的查看整个仿真过程。

b）建模复杂度低。Simulink工具箱包含强大的功能模块，用户只需根据信号的输入输出关系连接各功能块，即可建立复杂的仿真模型，与传统语言相比，大大降低了编程复杂度。

c）程序扩展性好。针对不同的空空导弹、作战条件及目标机动方式，在计算导弹攻击区时，只需要改变Simulink弹道仿真模型中各模块的相应参数。

该仿真算法已成功应用于某型空空导弹作战仿真系统研制，应用效果良好。

[1]胡朝晖，李东文，汪浩生.通用空空导弹攻击区仿真研究[J].弹箭与制导学报，2002，22（3）：18－23.

[2]逮宏亮，张艺瀚，李伟仁.基于RBF网络的导弹攻击区解算及对比分析[J].火力与指挥控制，2004，29（5）：47－50.

[3]崔晓宝，田秀丽，杜祥楚.格斗导弹攻击区分析数字仿真系统[J].航空兵器，1997（1）：13－17.

[4]冯戈利.机载中程空空导弹作战效能分析[D].西安：西北工业大学，2001.

[5]张志涌.精通 Matlab6.5版[M].北京：北京航空航天大学出版社，2003.

[6]刘代军，高晓光，李言俊，等.中远程复合制导空空导弹允许攻击区计算[J].航空兵器，1998（2）：1－5.

[7]李廷杰.导弹武器系统的效能及其分析[M].北京：国防工业出版社，2000.