基于双方最优控制的微分策略制导＊

罗 生，孙卫国，张 萍，杨永胜

（1上海交通大学航空航天学院，上海 200240；2中国空空导弹研究院，河南洛阳 471009）

0 引言

20世纪50年代，由于制导系统拦截飞行器的引入、人造卫星的发射和航天中有关机动追击问题的需要，美国数学家Isaacs[1]组织开展了对抗双方都能自由决策行动的理论追逃问题研究，取得了突破性的成果。1965年，Isaacs整理出版了世界上第一部微分对策著作《微分对策》。1971年，美国科学家Friedman[2]采用了两个近似离散对策序列精确定义了微分对策，建立了微分对策值与鞍点存在性理论，从而奠定了微分对策理论的数学基础。

微分对策因其理论上的最优性，已应用于战术导弹的制导律设计[3－4]。Tahk[5]等人设计利用梯度法求得微分对策制导的数值解，但模型极为复杂。Basar[6]设计了神经网络微分制导律，但不能实时计算。我国院士汤善同[7]采用微分对策强迫奇异摄动方法设计了零阶组合反馈制导律，这种制导易于弹上实时实现，但其是针对有强大地面雷达指示的防空导弹设计的。

文中采用伴随理论，解决终端控制的最优制导问题，避免了必须对矩阵方程式的直接求解，并通过仿真验证了所设计制导律的性能。

1 微分对策原理

1.1 最优控制模型

微分对策属于双边的最优控制问题，其状态方程可以写成：

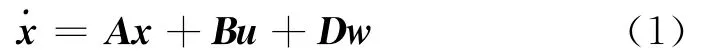
式中：x为状态变量；u为导弹控制策略；w为目标机动策略；A、B、D为状态矩阵。

初始条件：x（0）＝x0

性能指标函数：

式中：P（t）、R（t）、γ 为加权矩阵，t0为开始时刻，tf为终端时刻。

1.2 微分对策定义

假设在导弹发射后，拦截目标的某个时刻，目标和导弹都知道对方在此时刻之前的所有信息。如果导弹首先采取机动u1，然后目标根据导弹采取最优规避w1，指标函数为minumaxwJ ＝J（u1，w1）。这种条件下，导弹拦截目标将消耗最大能量，即有J（u1，w1）＝Jmax。如果目标不按照最优机动w1机动，即w≠w1，必有J（u1，w1）≥J（u1，w），即导弹消耗的能量J（u1，w）＜Jmax；相反，如果目标首先采用机动策略，则有J（u，w2）≥J（u2，w2），即J（u，w2）＞Jmin。

综合可知minumaxwJ≥minwmaxuJ，即存在：J（u1，w1）≥J（u2，w2）。当u1＝u2＝u＊、w1＝w2＝w＊时，有J（u1，w1）＝J（u2，w2）时，此时称（u＊，w＊）为鞍点，鞍点（u＊，w＊）实际上就是双方最优控制界栅点，微分对策实际上就是鞍点的求解，微分对策制导实际上就是假设目标根据导弹信息进行最优规避条件下来求解导弹的最优机动。

2 制导律的推导

2.1 制导模型

制导律模型如图1所示。

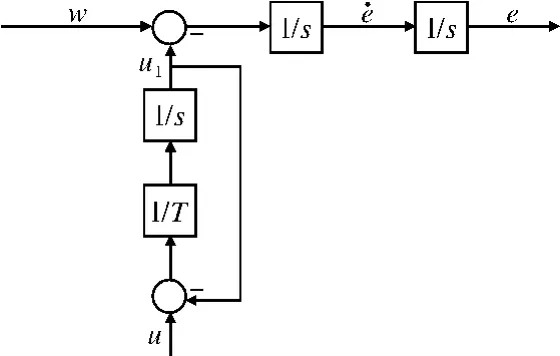
图1 制导律模型

其中：

状态矩阵：

只考虑对末端脱靶量进行要求，得：

则指标函数简化为：

2.2 制导律求解

对于单边最优的制导问题，可以应用施瓦茨不等式求出解析解，而对于微分对策的双边最优问题用这种方法是无法解决的。这里应用一种在脉冲仿真中常用的伴随方法对微分对策进行求解。

应用伴随理论，写出原系统状态方程的伴随方程：

其中伴随矩阵AT为：

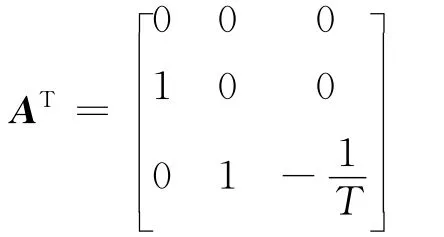
考虑末端只对脱靶量进行要求，则末端伴随状态为：

λ1（tf）＝bx1（tf），b为常数

λ2（tf）＝λ3（tf）＝0

因为λ1为常数，令λ1＝bx1（tf），则可得到：

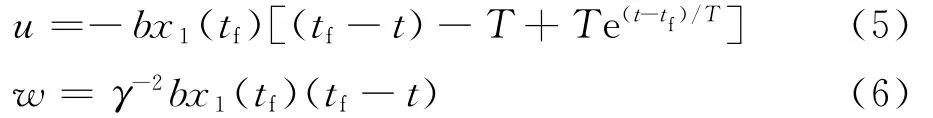
把方程（5）代入到状态方程（1）中，并对其进行积分运算，设可以得到微分对策制导律表达式为：

3 仿真验证

3.1 仿真条件

为了验证所设计微分制导律的性能，用Matlab搭建二维线性拦截模型，对理想比例制导（IPN）、单边最优制导（OPN）、微分对策制导（DOPN）进行仿真验证。

为了模拟强电磁空战中，导弹发射后可能无法准确获得目标信息的情况，这里假设制导律中没有目标加速度补偿。设弹目相对速度Vc＝700m／s、导弹过载限幅umax＝50g、一阶导弹时间常数T＝0.3s。

3.2 制导律模型

a）理想比例导引（IPN）：

b）单边最优（OPN）：

c）微分对策（DOPN）：

其中取：γ＝2.75；b＝1000。

3.2 目标机动模型

为了充分验证制导律对目标的截获能力，选取阶跃机动、正弦机动和B＿B机动作为评估基准，具体模型如下：

a）阶跃机动

w＝Ant

b）正弦机动

w ＝Antsin（ωt），取ω＝5rad／s

c）B＿B机动

仿真中目标机动幅值取：Ant＝9g。

3.3 仿真结果

在终端时间tf为1s和3s两种末制导情况下分别仿真。表1为三种制导律对于不同机动目标的脱靶量情况。

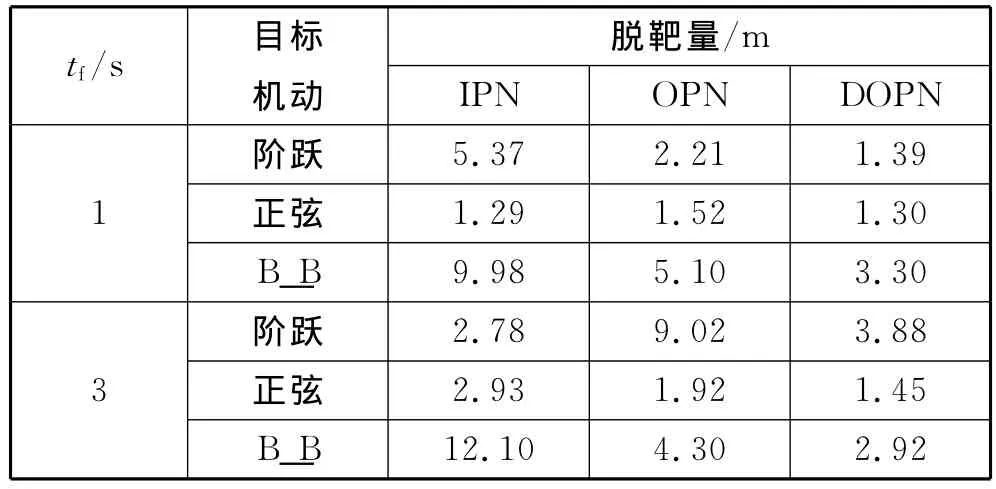
表1 三种制导律脱靶量

图2为目标阶跃机动情况下导弹过载响应和能量消耗曲线。

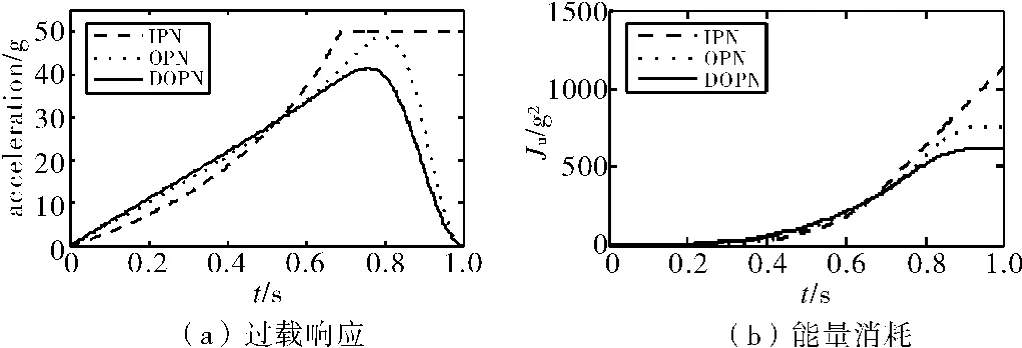
图2 目标阶跃机动下导弹过载响应、能量消耗

图3为目标在正弦机动情况下，导弹的过载响应曲线和能量消耗曲线。

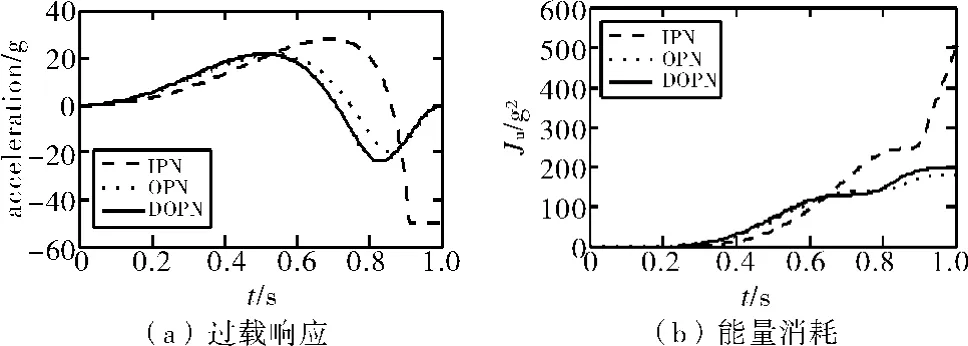
图3 目标正弦机动下导弹过载响应、能量消耗

3.4 仿真结果

从脱靶量上看，对于复杂目标机动，IPN和OPN表现出明显的不适应性，而DOPN则具有很强鲁棒性。从能量消耗的角度来衡量，IPN能量消耗大，而DOPN和OPN消耗能量小于IPN，并且DOPN还要小于OPN。

4 结论

文中应用伴随理论成功推导了基于双方最优策略下的微分对策制导律，并通过对目标三种不同典型机动的仿真，以及将仿真结果与比例导引、最优导引的对比，得出微分对策制导对多种形式的目标机动都具有很高的制导精度和小的能量消耗，是一种更高级的制导律，具有很大的应用前景。

但微分对策制导律也有其自身缺点，比如形式复杂，需要较多的精确信息，这些是影响微分对策能否成功应用的关键。

[1]Isaacs R.Differential games[M].New York：John Wiley＆Sons，1965.

[2]Friedman A.Differential games[M].New York：Wiley Interscience，1971.

[3]Cherry G W.A general explicit，optimizing guidance law for rocket－propellant spacecraft，AIAA 64－638[R].1964.

[4]Shaw R L.Fighter combat：the art and science of air－toair warfare[M].2nd ed.UK：Patrick Stephens Ltol，1988.

[5]M J Tahk，H Ryu，J G Kim.An iterative numerical method for a class of quantitative pursuit－evasion games[C]//AIAA Conference on Guidance，Navigation，and Control，1998：175－182.

[6]Basar T，Olsder G J.Dynamic noncooperative game theory[M].Philadelphia：SIAM，1999.

[7]汤善同.微分对策制导规律与改进的比例导引制导规律性能比较[J].宇航学报，2002，23（6）：38－42.

[8]张嗣瀛.微分对策[M].北京：科学出版社，1987.