基于单轴旋转的捷联系统误差特性分析*
2011-12-07孙伟,孙枫
孙 伟,孙 枫
(1辽宁工程技术大学测绘与地理科学学院,辽宁阜新 123000;2哈尔滨工程大学自动化学院,哈尔滨150001)
0 引言
长时间工作的捷联惯导系统,惯性测量元件的常值偏差将引起随时间积累的定位误差,它是影响惯性导航系统性能的重要因素[1-2],将惯性测量单元(inertial measurement unit,IMU)进行转动以调制惯性器件常值偏差是实现高精度惯性导航的有效方法之一[3-5],但是IMU的连续转动会激发出新的误差因素[6],引起系统定位误差。因此,文中针对转台转轴与当地垂线偏离及尺寸效应这两个误差因素对旋转捷联系统导航精度的影响进行分析与仿真。
1 IMU单轴旋转捷联系统误差抑制原理
捷联惯导系统单轴旋转自动补偿方法[7-9]是将安装有惯性器件的IMU相对载体坐标系(b坐标系,oxbybzb)旋转,使惯性器件的偏差沿着载体坐标系呈周期性变化。设oxsyszs为IMU坐标系,s坐标系是随着IMU位置改变而改变的一个时变坐标系。
设初始时刻IMU坐标系与载体坐标系重合,然后s系以角速度ω绕ozb轴旋转。采用地理坐标系作为导航坐标系。图1是以IMU单轴旋转为例说明自动补偿原理。
在t时刻,载体坐标系和IMU坐标系的夹角为ωt,两个坐标系之间的关系用方向余弦表示[10]:

图1 IMU坐标系与载体坐标系的相对位置关系
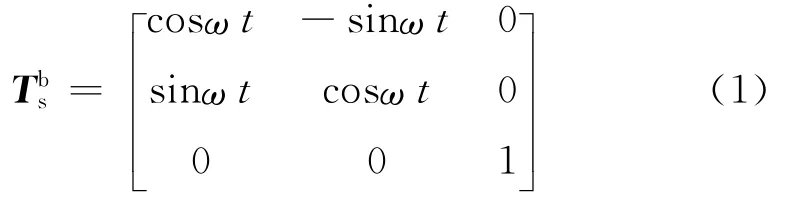
惯性器件的输出误差中一般包括常值偏差和随机偏差,常值偏差可以通过标定的方法进行补偿,但是这种常值偏差也呈现出变化的趋势,主要体现在逐次启动误差和逐日变化的误差,因此通过标定的方法不能将惯性器件的常值偏差进行完全的补偿。假设标定结束后陀螺仪和加速度计的误差模型为[11]:

式中:ε′、∇′分别表示陀螺仪和加速度计剩余常值误差;ε″、∇″分别表示陀螺仪和加速度计与系统工作时间相关的误差系数。
根据IMU旋转过程中s坐标系与b坐标系的相对位置关系,得到载体系下惯性器件偏差的调制形式:

由式(3)和式(4)可以看出,水平方向上惯性器件的剩余常值偏差被调制成周期变化的量,在一个转动周期内经过积分后为零,与时间有关的项经过积累后为常值,因此ozb轴引起的误差将随时间积累。除了惯性器件自身的误差因素外,旋转捷联惯导系统中转台转轴与当地垂线偏离及尺寸效应误差是影响导航精度的主要因素,下文围绕这两种误差对导航精度的影响机理进行分析。
2 转台转轴与当地垂线偏离
以单轴旋转为例,分析转台的转动轴与当地垂线存在夹角时对导航精度的影响。转台倾斜角的大小及倾斜角的方向具有任意性,为便于分析及不失一般性,假定α为转台平面与载体平面的夹角,β为平台倾斜取向与地理东向的夹角,得到旋转过程中s坐标系相对b系的位置关系,如图2所示。
根据图2描述的b系相对s系的位置关系,可以得到两个坐标系之间的关系用方向余弦Tsb表示:

图2 IMU旋转过程中s系与b系的相对位置

由于转台转动轴与地垂线不重合,在IMU的旋转过程中,3个陀螺仪均敏感到地球自转角速度在s坐标系上的分量;水平加速度计敏感到重力加速度在s坐标系水平方向上的分量:

如图2所示,s坐标系到b坐标系的转动过程:
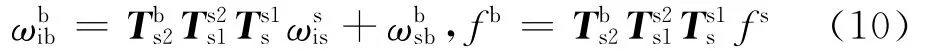
其中,两坐标系的转换关系可以用如下转换矩阵表示:

将式(8)和式(9)分别代入式(10),经过化简得到陀螺仪和加速度计的输出在载体系下的表示形式:

由式(12)可以看出,转台转轴与当地垂线偏离导致旋转角速度和方位陀螺漂移在水平方向上产生常值分量,水平方向上的陀螺仪敏感此分量。捷联矩阵Tnb的微分方程及Tnb与陀螺仪输出的函数关系分别如下:


通过对式(12)分析可得,在平台倾斜取向一定的条件下,台面倾角α越大,旋转角速度的水平分量越大,系统积累的误差就越大。加速度计的偏差在水平方向上产生投影,使水平方向上的均值不为零,即转动后加速度计的水平常值漂移得到部分调制。为了定性分析转台转轴与当地垂线偏离时引起的系统误差,忽略由于陀螺仪输出的变化导致捷联矩阵更新时产生的变化,即假定=I。则经过时间t′,IMU旋转过程中加速度计的输出经过积分得到水平速度误差为:
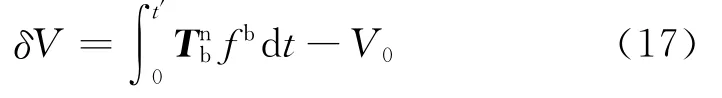
V0表示载体理想状态下的水平速度,其值为零。在水平通道内:
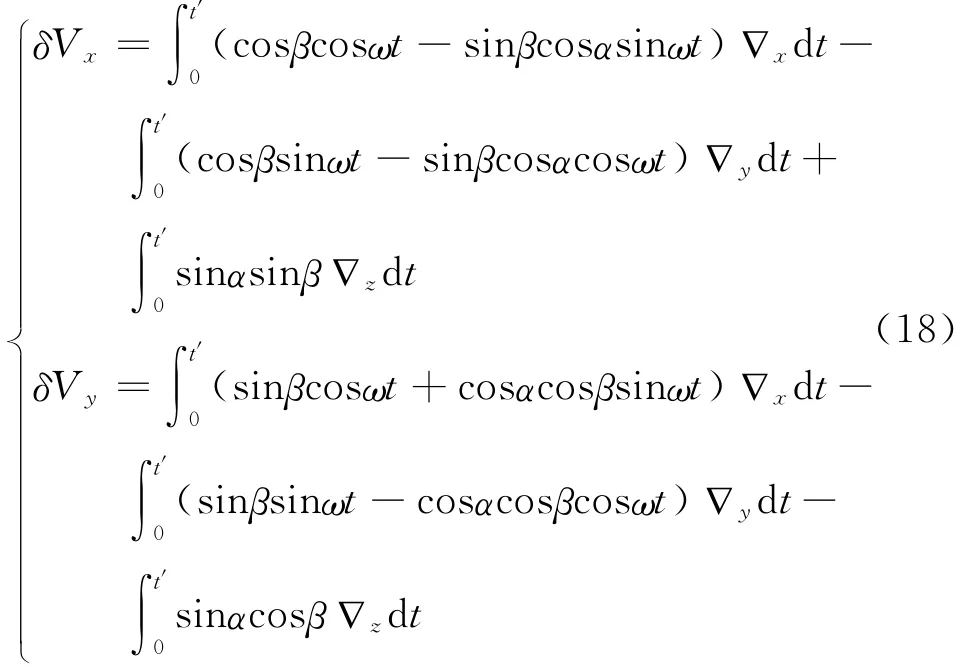
由式(17)可以看出,与时间有关的三角函数项经过一个周期的积分后为零,但是反映在速度上,引起速度的周期性波动,周期为IMU的旋转周期;由于旋转机构的转动轴与地垂线偏离,方位陀螺仪漂移在水平方向上产生分量,导致速度误差表现为随时间持续增长。
3 尺寸效应误差
当加速度计偏离理想位置和IMU处于转动状态时,离心加速度和切向加速度的存在引起加速度计的测量误差。加速度计输出误差的表达式为[12]:

式中第一项表示切向加速度的影响,第二项表示向心加速度的影响。
由于IMU安装在载体上,假设IMU坐标系和b坐标系具有同一个水平面,此时不用考虑IMU方位轴上加速度计的尺寸效应。将两个水平加速度计构成一个测量组件,可得到惯性测量组件的尺寸效应误差为:
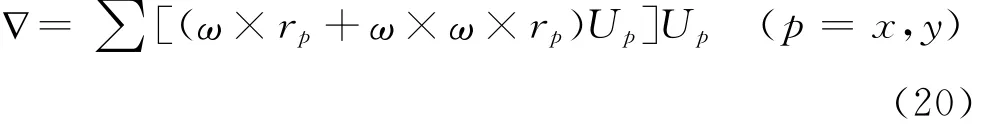
如图3,对于每个加速度计的位置矢量rp能分解为两个分量r和dp,r是IMU坐标系上的加速度计组件中心p的位置矢量;dp是加速度计ax相对于IMU坐标原点的位置矢量,因此有:

图3 尺寸效应几何分析图

式(21)代入式(20):

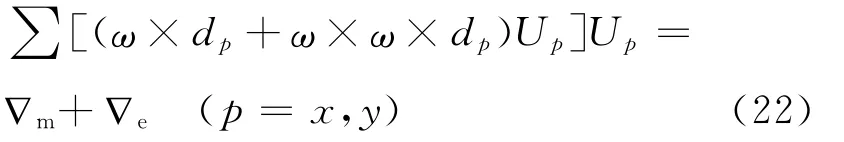
式(22)中第一项是由于r不等于零引起的,称为“惯性测量组件的安装偏差尺寸效应”用∇m表示;第二项是由于dp不等于零引起的,称为“加速度计的尺寸效应”用∇e表示。其中惯性测量组件的安装偏差可以通过在线标定补偿,文中主要讨论IMU连续转动过程中加速度计尺寸效应产生的影响,假定水平方向上的加速度计到IMU坐标原点的距离均为dp,则加速度计的输出表示为:

IMU转动过程中,旋转角速度的不平稳导致水平加速度计输出是一个带有随机振荡的量。为便于分析问题,假设载体始终处于静止状态,有Tnb=I得到导航系下加速度值为:

水平加速度计偏差在一个完整的周期内完全得到调制,与旋转角速度有关的项由于伴随有随机量导致一个周期内不能完全得到调制,因此旋转角速度在水平方向上产生了不对称的常值,通过对加速度的积分得到载体速度误差和位置误差。
4 仿真分析
为验证转台转轴与当地垂线偏离及尺寸效应误差对旋转捷联系统导航精度的影响,利用VC++开发工具构建这两种条件下的捷联惯性导航系统模拟器及解算过程,根据仿真结果验证上述两种误差因素对系统导航精度的影响。
4.1 转台转轴与当地垂线偏离仿真
仿真条件:静基座导航,初始地理位置为北纬45.7796°、东经126.6705°,转台转轴与当地垂线夹角为0.001°,为了问题分析的简单化,倾斜角取向为沿导航坐标系东西向。IMU旋转角速度为6°/s,加速度零位误差10-4g,暂不考虑陀螺漂移和其它误差因数,仿真时间24h。
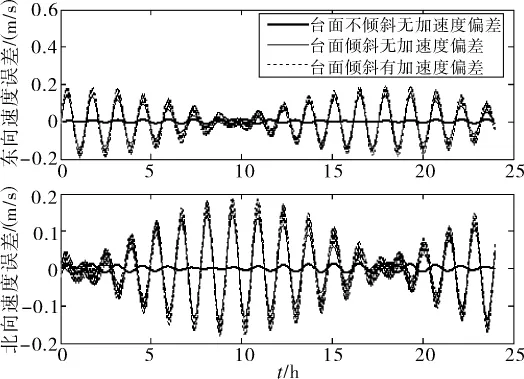
图4 IMU旋转过程中不同条件下系统水平速度误差曲线
下面对图4进行分析。理论上讲,根据式(17),当转台倾角取向沿导航系东西方向,由倾角取向定义得β=0°,在一个旋转周期内方位陀螺漂移得到积累,引起北向速度产生常值误差;加速度计零位偏差在一个转动周期内得到调制,但是引起速度误差的周期振荡。仿真结果验证了这一点:无加速度计零位偏差时,台体倾斜导致水平速度产生舒勒周期和傅科周期振荡;在转台平面倾斜的条件下,无加速度零位偏差导致系统中不产生旋转周期,有加速度零位偏差导致舒勒周期中存在旋转周期。
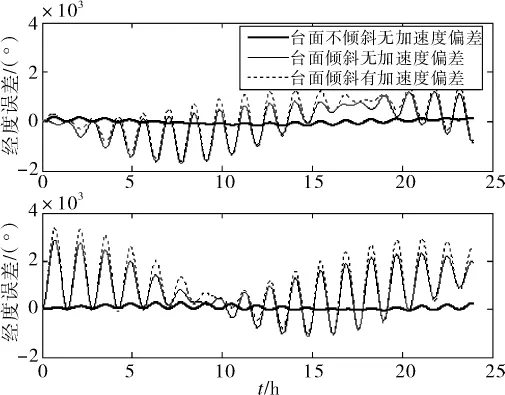
图5 IMU旋转过程中不同条件下系统位置误差曲线
旋转角速度在导航坐标系oxb轴上的投影被东向陀螺感知,这一分量引起常值经度误差,如图5所示。为了直观反映出载体在不同误差条件下的定位精度,根据定位误差计算公式(25)计算出不同时刻系统的位置误差,如图6所示。
式中:R 表示地球半径;L 表 示当地纬度;λ表示当地经度。经对比发现:同转台转轴与当地垂线重合时相比,偏离时会引起定位误差,达到0.12nmile以上;在转轴与地垂线偏离的条件下,通过对比定位误差可以看出:与没有加速度计偏差时的定位误差相比,有加速度计偏差时产生的定位误差多出0.02nmile,验证了式(14)的正确性。
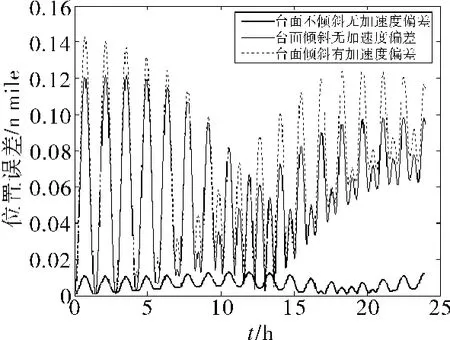
图6 IMU旋转过程中不同条件下系统定位误差曲线
4.2 尺寸效应误差仿真
仿真条件:IMU转动角速度6°/s,转速误差为10-5,加速度计到坐标原点的距离为0.1m,初始位置同4.1,不考虑任何其它误差因素。

图7 有无尺寸效应时载体姿态误差曲线
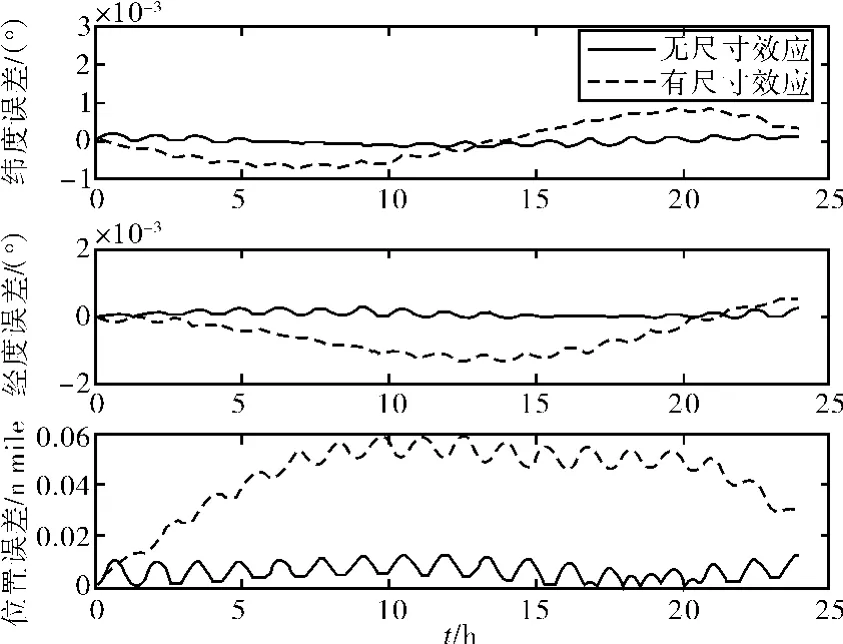
图8 有无尺寸效应时载体定位误差曲线
IMU转动过程中,尺寸效应引起的向心加速度参与惯导解算导致水平姿态角产生常值偏差,转动角速度的不平稳同时引起陀螺仪的输出是非对称的,在一个转动周期不能将其完全调制,导致姿态误差加剧;转速的不平稳同时引起加速度计的输出在导航系上的分量不能得到完全调制,如式(20),激发出导航系统的位置误差。如图8所示,24h的仿真过程中最大可以达到0.06nmile,大于无尺寸效应时的导航误差。
5 结论
文中概述了旋转捷联惯导系统的误差抑制机理,分别针对转台转轴与当地垂线偏离、尺寸效应对系统导航精度的影响进行了理论推导、分析与仿真。通过对比仿真结果可以看出当转台转轴与当地垂线偏离时产生了0.14nmile的定位误差,远大于转轴与地垂线重合时的位置误差;虽然尺寸效应引起的定位误差远小于转轴与地垂线偏离所引起的定位误差,但是转动角速度的不平稳仍然会激发出0.06nmile的位置误差。目前旋转式捷联惯导系统处于实验室阶段,如何设计合理的误差补偿措施是本实验室下一步的主要工作。
[1]于旭东,王宇,张鹏飞,等.单轴旋转对惯性导航系统误差特性的影响[J].中国惯性技术学报,2008,16(6):643-648.
[2]Ishibashi S,Tsukioka S,Sawa T.The rotation control system to improve the accuracy of an inertial navigation system installed in an autonomous underwater vehicle[C]// Workshop on Scientific Use of Submarine Cables and Related Technologies 2007,2007:495-498.
[3]Morrow R B,Heckman D W.High precision IFOG insertion into the strategic submarine navigation system[C]//IEEE 1998Position Location and Navigation Symposium,1998:332-338.
[4]Levinson E,Willcocks M.The next generation marine inertial navigation is here now[C]//IEEE Position Location and Navigation Symposium,1994:121-127.
[5]孙枫,孙伟.旋转捷联惯导系统精对准技术研究[J].系统工程与电子技术,2010,32(3):630-633.
[6]黄昆,王戈,杨功流,等.旋转式捷联惯导系统的误差特性分析[C]//中国惯性技术学会第六届学术年会论文集,2008:56-61.
[7]袁保仑,饶谷音.光学陀螺旋转惯导系统原理探讨[J].国防科技大学学报,2006,28(6):76-80.
[8]孙枫,孙伟.旋转自动补偿捷联惯导系统技术研究[J].系统工程与电子技术,2010,32(1):122-125.
[9]孙枫,孙伟,郭真.基于IMU旋转的捷联惯导系统自补偿方法[J].仪器仪表学报,2009,30(12):2511-2517.
[10]孙枫,孙伟.摇摆基座下旋转捷联系统粗对准技术研究[J].仪器仪表学报,2010,31(4):929-936.
[11]刘峰,徐策,尚克军,等.水平初始对准误差对旋转IMU导航系统的精度影响[J].中国惯性技术学报,2008,16(6):649-656.
[12]张树侠,孙静.捷联式惯性导航系统[M].北京:国防工业出版社,1992.
