超低渗透率测量仪的测试标定及初步测量结果

吴 曼 杨晓松 陈建业

(地震动力学国家重点实验室，中国地震局地质研究所，北京 100029)

超低渗透率测量仪的测试标定及初步测量结果

吴 曼 杨晓松*陈建业

(地震动力学国家重点实验室，中国地震局地质研究所，北京 100029)

低渗-超低渗透率测量是流体渗流力学和岩石物理学研究领域的热点问题。断层带流体输运的定量化研究对于了解断层的力学性质和预测地下流体的流动具有重要意义。文中介绍了新研制的超低渗透率测量系统和工作原理。这套设备使用稳态法和目前逐渐流行的孔隙压力振荡法进行测量，其孔隙流体为蒸馏水和氮气，最高围压可达200MPa，孔隙压上限为40MPa。对该测量系统进行了参数标定，并给出了循环加载条件下典型砂岩的渗透率测量结果。对比了2种测量方法得到的结果，分析了产生差异的原因，比较了2种方法的特点和适用条件。探讨了孔隙压力变化对实验结果的影响，按照加载间隔计算了有效压力系数。结果发现有效压力系数依赖于加载路径。使用最小二乘法对所有数据进行拟合，求出了最优有效压力系数并获得渗透率和有效压力函数关系，为分析围压和孔隙压对渗透率的影响提供了依据。

渗透率测量 振荡法 稳态法 有效压力

0 引言

岩石作为一种多孔介质，包含着大量的微裂隙与孔隙。各种流体在多孔介质中流动是岩石中物质输运最重要的过程。该过程对环境科学、地震构造(流体的进入改变了孕震区的应力状态，影响到地震发生的机理)、石油地质(油气的运移和储存)等都有重要影响。渗透率是描述岩石输运特性的最重要的参数，它表示流体流过岩石的容易程度，是制约输运过程的关键物理参数。对于同一类岩石，由于其生成环境和内部结构的不同，其渗透率的变化可以达几个数量级;而对于不同类型的岩石，其渗透率变化范围则更大，可以达近10个数量级(Brace，1980)。其中，超低渗透性岩石的测量一直是研究的难点。例如，对于富含黏土矿物的岩石(如泥岩和断层岩)和孔隙度极低的岩浆岩和变质岩，其渗透率通常很低，利用常规的稳态测量方法难以进行精确测量。另外，建立稳态流动需要很长的时间而导致测量效率低下，甚至根本无法测量出样品的渗透率。但是低渗-超低渗岩石渗透率的精确测量日益受到重视。例如，随着近年来对低渗透油田的开发，低渗透储层中渗流的特性和规律引起了人们的重视(杨琼等，2004)。地震孕育及发生、地震断层带的复发等与断层带中流体渗透性密切相关(Bernade et al.，1982;陈颙等，2009)。渗透率测量的另2种方法(脉冲法和振荡法)则能够对低渗样品进行精确测量。为研究汶川地震断层岩的渗透性对流体迁移、断层的愈合、断层的摩擦强度等的影响，分析其与强震孕育环境的关系，中国地震局地质研究所与山东中国石油大学石仪科技有限公司联合研制出多工作方式(稳态及非稳态测量方式)的超低渗透率测量系统，其渗透率测量下限达到10-21m2。本文系统介绍该设备的测量原理及方法，并给出该测量系统的一系列标定参数。在此基础上，对多种砂岩的渗透率开展了初步研究，获得了有意义的结果。

1 渗透率测量原理及方法

实验室测量渗透率的方法有稳态法、脉冲法(Brace等，1968)和振荡法(Kranz，1990)。稳态法即在样品的上、下游端施加稳定的压力差ΔP，通过测量流经样品的流量Q，依据达西定律计算渗透率k=(QηL)/(ΔPA)。其中L为样品长度，A为样品横截面积，η为流体的黏滞系数。稳态法主要适用于测量渗透率较高的岩石，例如k＞10-17m2的岩石(Bernabe，1987;Zhu et al.，1997)。

脉冲法最早是由Brace(1981)提出的，后经Hsieh(1981)和Neuzil(1981)改进加以推广。其测量原理为在原有的稳定孔隙压P2状态下，通过在样品的上游端突然施加一个孔隙压力脉冲，造成样品的上游端和下游端之间瞬间存在附加的压力差(设此时上、下游端瞬间压力分别为P1和P2)，随着流体在样品中的流动，上、下游端压力逐渐衰减，并遵从P1(t)=Pf+(P1-Pf)·e-αt，P2(t)=Pf-(Pf-P2)·e-αt的变化规律，其中 α为衰减系数，Pf为达到新的平衡状态时的压力。介质的渗透率k与衰减系数成正比(Brace等，1968)。通过测量样品上、下游端的压力随时间的变化可以求得衰减系数α，进而计算出介质的渗透率。

振荡法最早是借鉴于热扩散系数测量而提出(Cowan，1961)，即在岩心的上游端施加特定的振荡压力，通常为正弦振荡。由于样品的渗透性，在样品的下游端会出现压力的响应。该响应通常表现为相位延迟(即存在相位差θ=θd-θu＜0，θd为下游相位，θu为上游相位)和振幅减小(用下游端压力振幅Ad与上游端压力振幅Au之比α度量，α=Ad/Au＜1)(图1)。渗透率k和比储流率βs可以通过下式求得:

图1 孔隙压振荡法原理图Fig.1 Schematic diagram of pore pressure oscillation method.

式中:η、L、T和A分别为流体黏度、样品长度、压力振荡周期和样品的横截面积;Bd为下游端储流系数，被定义为单位压力的改变所引起的流体体积改变量，单位为m3Pa-1，该参数需要通过测量进行严格的标定;Ψ和γ为引入的两个无量纲参数，均为α和θ的函数(Kranz et al.，1990;Fischer et al.，1992)。由公式(1)和(2)可见，通过测量α和θ可以确定样品的渗透率和比储流率(推导见附录A)。压力振荡法测渗透率属于一种非稳态方法，非常适用于低渗-超低渗岩石样品的测量，具有测量精确、快速简便的优点。

2 超低渗透率测量仪结构、实验试样及流程

2.1 超低渗透率测量仪结构

地震动力学国家重点实验室拥有的超低渗透率测量仪包括:围压系统、孔隙压系统、样品腔、中间容器、回压系统和数据采集处理系统(图2)。围压系统由高压泵和增压器组成，增压器的增压比为6.25:1，高压泵可以采用自动和手动两种控制方式，能够提供的最大静水围压为200MPa，传压介质为纯净水。孔隙压系统由2台高精度柱塞泵组成，能够不间断地以压力和流量两种控制方式驱动孔隙流体。当以压力控制方式工作时，系统可提供振荡周期为20～2,400s的正弦压力或恒定压力。样品为圆柱状，直径为20mm，长度介于3～50mm。本设备设计安装了2个中间容器(气体中间容器和液体中间容器)，通过中间容器与孔隙压驱动系统连接可以为系统提供不同的孔隙流体介质。另外，中间容器还具有缓冲和平滑压力波动的作用。数据采集处理系统主要包括压力计量模块，出口流量计量模块及数据处理模块。压力计量模块采用精密压力表(精度为0.1%)和压力传感器(精度为0.08%)同时计量。当选择稳态流动实验时，利用出口流量计量模块(由0.001g测量精度的电子天平和数据采集系统组成)测量通过样品的流量。当以纯净水为工作介质时，该设备的渗透率测试范围为10-14～10-21m2。

图2 实验测量装置示意图Fig.2 Sketch map of ultralow permeability test equipment.

2.2 试样特征

为了对超低渗透率测量仪测量结果的一致性、稳定性和精度进行标定，确定其各项技术参数，选择了3种砂岩试样进行实验。试样的基本特征参数列于表1。另外，需要通过对比振荡法与稳态法的结果，来对振荡法的效果进行考察，确定其是否存在系统误差，为此选择渗透率适合于用稳态法和振荡法进行测量的试样，其渗透率为(1.03～2.4)×10-17m2。

2.3 实验流程

实验前将样品在80℃烘箱中烘干至恒重，然后进行密度和孔隙度的测定。在开始进行渗透率测量之前，对样品进行抽真空、水饱和处理12h以上。振荡法测量按以下5步进行:第1步加载围压(Pc)至40MPa。第2步加载正弦振荡孔隙压(Pp)，一般情况下加载Pp的平均值(P0p)到35MPa(Pp加载需要满足10MPa＜P0p≤ Pc-5MPa条件)，Pp的振幅为P0p的10%～20%。依据样品渗透率的高低，选择不同的振荡周期和Bd值。第3步，在下游端的正弦波响应达到稳定后测量下游端与上游端信号的振幅比(α)和相位差(θ)2个参数、采集数据和计算渗透率。第4步，按5MPa的间隔改变孔隙压，即在P0p=35、30、25、20和15MPa孔隙压条件下测量渗透率。第5步，按一定间隔(通常为20MPa)逐步增高围压至180MPa，在每次增压之后按上述第3和第4步骤进行类似的测量。

稳态法的测量步骤同样分为5步。第1步，加载围压(Pc)至10～40MPa。第2步在样品的上游端加载恒定孔隙压力(Pp)(Pp≤Pc-1MPa)，可以依据不同样品的渗透性选择不同的孔隙压力，如测量渗透率较高的样品(例如k≥10-16m2)时，孔隙压力选择10MPa即可;测量中低渗样品(k≤10-17m2)时，孔隙压力则可以选择25～35MPa，以减少达到稳流所需要的时间和增大渗流流量。第3步，设定各项采集参数，包括流量计量跨度，选择非连续滴液，待出口计量模块中驱替排量达到稳定后，采集通过样品的流量，利用达西定律计算样品的渗透率。第4步，改变样品上游端的孔隙压力并分别测量其渗透率。第5步，按一定间隔(通常为20MPa)逐步增高围压至180MPa，再以同样的间隔卸压至10MPa，并进行多次循环，在每次增压之后按第3和第4步骤进行测量。

3 测量结果

3.1 下游储流系数(Bd)值标定

从公式(1)和(2)可以看出，利用振荡法测量样品的渗透率需要知道下游端储流系数(Bd)。精确地标定Bd值是获得高质量渗透率测量结果的前提。由于直接测定Bd值很困难，而测量总储流系数(Bw)和上游端储流系数(Bu)相对容易，因此通过精确测定Bw和Bu来计算Bd值。另外，考虑到渗透率的振荡法测量精度与Bd值的选取相关，测量较低的渗透率时，需选取较小的Bd值。为此专门定制了不同孔隙体积的标准体积块，并标定了各个标准体积块的Bd值，以适用于利用振荡法测量不同渗透率样品。Bd值的标定分为3个步骤:第1步，用实心垫块填满样品腔，打开连接上游端和下游端的旁通阀，在不同的孔隙压力下测出整个样品腔上游端和下游端管线及阀门等所有能够容纳流体的部分体积的变化，得到总储流系数(Bw);第2步，关闭连接上游端和下游端的旁通阀，以相同的方法测出上游端的相应储流系数(Bu);第3步，将二者测量结果通过数据拟合并相减得到相应的下游端储流系数(Bd)。依据储流系数与压力的关系，我们采用幂律方程B=A·Pb+C进行数据拟合，拟合系数的置信度为95%，标定结果如图3所示。数据结果显示，当孔隙压力低于10MPa时，Bd值随孔隙压力的增大而迅速减小;但当孔隙压＞10MPa时，Bd值趋于稳定。由于利用振荡法测量样品的渗透率时，孔隙压力通常有10%～20%的波动，因此进行渗透率测量时其孔隙压力不应低于10MPa。

图3 Bd值标定结果Fig.3 Calibration result of storage capacity parameter.

3.2 振荡法与稳态法重复性实验

在多次加载和卸载围压进程中对S005样品进行了稳态法渗透率测量，测量过程中孔隙压恒定为30MPa。实验结果表明，随着加载和卸载次数的增加，渗透率值逐渐下降 (图4，表2)，其变化幅度达到1个数量级。另外，在围压和孔隙压力都不变化的条件下，考察稳态法测量结果与时间的关系。结果显示，随着时间的推移，其渗透率呈现逐渐降低的趋势。

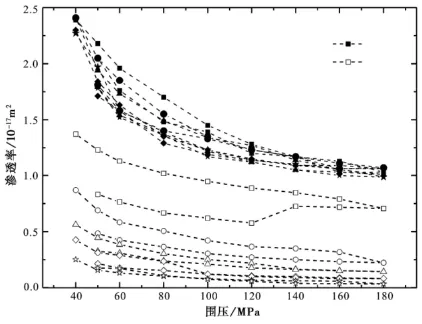
图4 稳态法和振荡法测量渗透率结果的稳定性Fig.4 Experimental permeability resultmeasured by both methods:steady-statemehod and pore pressure oscillation method.

在与稳态法相同的条件下，利用振荡法对同一样品进行渗透率测量。结果表明，随着加载和卸载次数的增加其渗透率没有系统地和有规律地增加或减小，测量的重复性很好(图4，表2)。5次加载和卸载循环测量结果的离散度介于2%(140MPa)～6%(40MPa)(图5)。对比两种测量方法发现，振荡法的测量结果稳定性和重复性明显优于稳态法。

利用振荡法对超低渗透泥质粉砂岩S009进行了循环加载的渗透率测量。结果表明，其渗透率稳定性很好，在水介质条件下的测量下限＜5×10-21m2(图6)。另外，对下游端压力响应信号的分析表明，即便渗透率已经＜5×10-21m2，但其噪声依然较小，信噪比较高，显示渗透率测量下限还有进一步下延的空间。该组实验至少表明，利用纯净水作为孔隙流体可以对10-21m2量级的超低渗岩石样品进行精确可靠的测量。

4 讨论

4.1 测量流程和时间对实验结果的影响

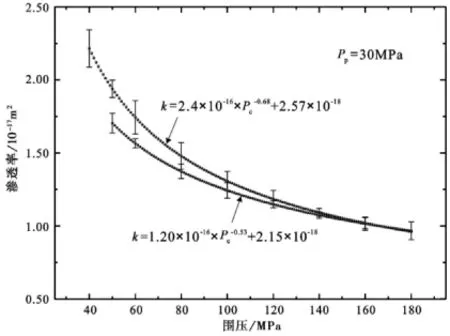
图5 砂岩S005振荡法渗透率测量误差标定结果Fig.5 Calibrating accuracy result of permeabilitymeasurement in pore pressure oscillation on sandstone S005.

在围压加载的过程中，由于孔隙及微裂隙的逐渐关闭，渗透率值逐渐减小，且渗透率-围压关系符合幂率分布;而在围压卸载的过程中，由于孔隙及裂隙的逐渐张开渗透率逐渐回升。从振荡法测量结果可见，多次加载和卸载循环过程并不会明显改变样品的渗透率。这表明样品随压力变化而产生的变形基本上是弹性变形，即在实验时间内卸载可以使样品基本恢复原状。那么在加载和卸载围压实验进程中，利用稳态法测量得到的渗透率却逐渐变小的原因何在呢?推测出现这种情况的原因可能在于流体在岩石渗流过程中冲刷孔壁导致微小颗粒迁移并堵塞样品喉道。稳态法测量中，渗透率值随测量时间增长而逐渐降低间接地佐证了这种推断(如图7)。对比利用振荡法进行的多次加载和卸载围压循环过程中所测量的结果发现，多次加载和卸载循环并不会对测量结果造成系统的影响。另一方面，虽然由于多次加载和卸载循环，实验时间持续了一周多，但实验时间并未对实验结果造成影响。

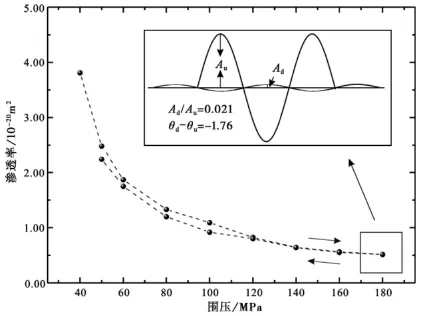
图6 超低渗样品(S009)渗透率与围压关系测量结果Fig.6 Relationship between permeability and confining pressure on ultralow permeable argillaceous siltstone.

利用幂律方程分别对振荡法加载和卸载的所有循环结果进行了拟合(图5)，得到如下拟合方程:kload=2.40×10-16×P-0.68c+2.57×10-18，kunload=1.20×10-16×P-0.53c+2.15×10-18(kload和kunload单位为m2，Pc单位为MPa)。测量结果与拟合曲线的最大偏差为1.8%～6.4%，并且总体而言，随着压力的增加，其最大偏差逐渐减小。从实验数据可以看出，振荡法测量结果具有很好的一致性。

4.2 有效压力系数求解

介质的渗透率同时受到围压(Pc)和孔隙压力(Pp)的影响 (图8)。随着围压的升高，渗透率逐渐下降;相反，当孔隙压力增加时，其渗透率升高，即孔隙压力有“抵消”围压效应的作用。另外，为了提高测量精度和缩短实验时间，在实验室进行渗透率测量过程中常使用比地壳中高得多的孔隙压力差。因此，通常使用有效压力(Peff)来描述围压及孔隙压对介质渗透性的综合作用。有效压力最简洁和被广泛使用的形式为Peff=Pc-Pp。然而理论和实践中发现这个定律并不总是适用(Nur et al.，1971;Walsh，1981)。更普遍适用的有效压力定律为Peff=Pc-λ·Pp，其中λ为有效压力系数，它度量了渗透率对孔隙压和围压的敏感程度(Bernade，1982;Li et al.，2009)。有效压力系数依赖于样品的孔隙度、孔隙的几何结构、岩石的矿物成分及其几何排列。此外，围压、孔隙压等也会显著影响有效压力系数。到目前为止已有大量关于有效压力定律的实验研究(Morrow et al.，1986;Warpinski et al.，1992;Kwon et al.，2001;Ghabezloo et al.，2009)。实验结果表明，Barre花岗岩的有效压力系数为0.56或0.91，Chelmsford花岗岩为0.6～0.7，Berea砂岩为2.2或4.0。根据岩石体积应变的有效压力定律可知有效压力系数λ=1-βs/βd，其中βd为含孔隙岩石的压缩系数，βs为岩石基质的压缩系数，因而一般情况下有效压力系数是＜1的。然而，对于不同的物理量有效压力系数并不是一样的。Berryman(1992a，b)系统分析过该问题，并推导出了分别适用于孔隙度、孔隙体积和流体量的有效应力定律。研究中发现对于富含黏土矿物的砂岩的有效压力系数往往显著＞1。

图7 稳态法测量中渗透率随时间变化的关系Fig.7 Relationship between permeability and time in steady-statemethod.

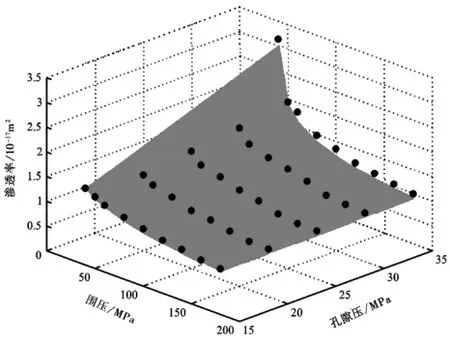
图8 砂岩S005样品渗透率与围压和孔隙压的关系Fig.8 Relationship between permeability，confining pressure and pore pressure on sandtone S005.

研究表明，对于渗透率而言，其有效压力系数可用如下方式求解λ=-(∂kp/∂pp)/(∂kc/∂pc)(Bernade，1986)。∂kp/∂pp刻画了在围压保持恒定的情况下孔隙压的变化所引起的渗透率变化;∂kc/∂pc为孔隙压保持恒定的情况下围压的变化所引起的渗透率变化(Bernade，1987;Al-Wardy et al.，2004)。本文考察ΔPc=20MPa和ΔPp=20MPa引起的k值变化，并计算 λ=-Δkp/Δkc。计算表明，λ随围压的增大而减小，其值介于1～2.3之间。利用最小二乘法在整个围压和孔隙压变化域对渗透率实验数据进行幂律函数的曲线拟合，获得幂律方程k=A·(Pcλ·Pp)b+C的各参数以及有效压力系数λ值。对S005试样的振荡法实验数据进行了拟合，其结果为:k=4.16Peff-017-0.78，Peff=Pc-1.1Pp(图9)。有效压力系数接近1表明，S005试样的渗透率对围压和孔隙压的敏感程度几乎一致。对于S007样品的测量结果，采用指数函数进行拟合的效果明显优于幂次函数，所得其有效压力系数λ为3.01(图10，11)。

图9 砂岩S005样品渗透率与有效压力的关系Fig.9 Relationship between permeability and effective pressure on sandstone S005.

4.3 稳态法与振荡法测量结果对比及启示

对比稳态法和振荡法的测量流程与结果，可以看出二者之间存在以下3个不同特征。

图10 砂岩S007样品渗透率与围压和孔隙压的关系Fig.10 Relationship between permeability，confining pressure and pore pressure on sandtone S007.

图11 砂岩S007样品渗透率与有效压力的关系Fig.11 Relationship between permeability and effective pressure on sandstone S007.

(1)两种测量方法分别适合于不同渗透率的样品。稳态法适合于测量渗透率相对较高的样品，实验表明，对于k≥ 10-18m2的样品，稳态法能够获得可靠的结果。但对于渗透率k＜10-18m2的样品，诸多因素可能会影响测量结果的质量并且实验时间非常漫长。首先，测量系统建立稳态流动需要很长的时间(甚至无法达到稳态平衡);其次，由于流量非常小，渗透一滴液体(约0.05g)的时间长达30min甚至1～2h，液体的蒸发直接影响到流量测量的精度(尽管在数据采集和防止蒸发方面采取了多种措施，仍然不能完全消除其影响)。相对于稳态法，振荡法更适合于测量低渗-超低渗透率样品。对于渗透率较高的样品(k＞10-16m2)，由于下游端压力响应与上游端的振荡压力的相位延迟(θ)和振幅衰减幅度均很小，从而导致计算渗透率的误差增大。而对于低渗-超低渗透率样品，利用振荡法可以较快地在样品上游端和下游端建立动态响应，产生显著的相位延迟和振幅衰减，因此能够在较短的时间内获得满意的测量结果。对于k≤10-20m2的样品，振荡周期T应选择＞960s(Fischer，1992)，振荡10个周期后下游端响应通常达到稳定状态，则160min可获得一个渗透率测量结果，进行一次加载和卸载围压循环测量大约需要45h。对于k≥10-17m2的样品，则振荡周期选择50s即可，约9min即可获得一个测量结果，进行一次加载和卸载围压循环并测量大约需要2.4h。目前，利用振荡法能够对渗透率k＜10-16m2的样品进行可靠的测量(蒸馏水为孔隙介质)。

(2)实验结果对实验持续的时间响应不同。稳态法的测量结果表明，渗透率随着测量时间的推移而逐步变小(图7)。造成这种现象的原因可能与流体在试样中流动时带动细小颗粒运移并堵塞孔隙流通喉道过程有关。随着实验时间延长，这种过程的累积作用逐渐增强，导致试样的渗透率逐步下降。由此可见，利用稳态法进行测量时，第1次加载所测量的结果最能反映样品的真实渗透性。相比而言，由于在振荡法测量过程中并没有孔隙流体的流动，因此，实验结果不受实验时间的影响，可以进行多次加载和卸载循环条件下的多次测量，从而获得很可靠的实验结果。

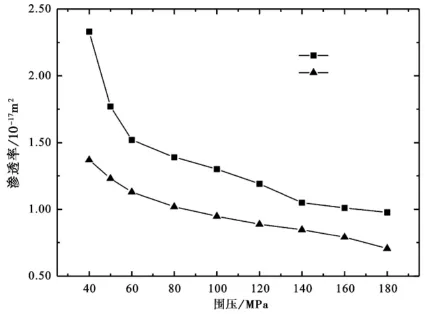
图12 振荡法与稳态法渗透率测量结果比较Fig.12 Comparison of permeability resultmeasured by both methods:steady-statemehod and pore pressure oscillationmethod.

(3)两种测量方法所获得的测量结果存在系统的偏差(图12)。对比发现，振荡法的测量结果比稳态法测量结果高出26.3%～58.8%(渗透率量级为10-17m2)。产生测量偏差的原因可能来自于两种测量方法的不同。在稳态法测量中，存在稳定流动的孔隙流体与流体通道壁的摩擦作用。而这种摩擦作用对振荡法测量结果影响很小(振荡法测量过程中没有孔隙介质流动)。此时，可将孔隙流体视为理想流体，设其在管道中的流动速度为v1，单位时间内通过单位面积上的流量q1=ρ·v1;而在稳态法测量中，由于流体分子的迁移显著地受到摩擦作用的影响，导致了孔壁附近的流体流动速度趋于零，中间位置的流体流动速度最高，因此其平均速度v2小于理想流体的流动速度v1，则单位时间内通过单位面积的流量q2=ρ·v2＜q1。由此可见，振荡法测量所得出的渗透率结果明显会高于稳态法的测量结果。当管道横截面积逐渐增大时，即岩样内部孔径增大时，流体分子与孔壁之间的摩擦作用逐渐减小，此时振荡法与稳态法测量结果可能就会逐步接近。

5 结论

(1)新型超低渗透率测量仪的标定测试结果良好，利用这套设备可以进行流体的稳态渗流以及使用孔隙压力振荡方法测试不同渗透率量级的岩石样品，测试过程快速简便，测试结果稳定。目前，利用振荡法本实验系统能够对渗透率k＜10-16m2的样品进行可靠的测量(纯净水为孔隙介质)，渗透率测量下限达到5×10-21m2，稳态法则适用于k＞10-18m2的岩石样品。

(2)振荡法与稳态法加卸载围压过程中，在恒定孔隙压条件下，渗流场与应力场均具有较好的相关关系。稳态法的测量结果表明，由于细小颗粒堵塞喉道，渗透率随着测量时间的推移而逐步变小。振荡法多次测量结果稳定，重复性较好，但一般高于稳态法测量结果。

(3)无论在稳态法还是振荡法的测试中，孔隙压力均对实验结果有明显的影响，砂岩渗透率对于围压及孔隙压均较敏感。利用最小二乘曲线拟合能够获得有效压力系数λ，使得渗透率测量结果与有效压力具有较好的相关关系。

致谢 何昌荣研究员在设备设计过程中给予了多方面的帮助和建议，中石大石仪科技有限公司的邵东亮、郑明军、王建强及何俊海参与了设备的设计并负责了该设备的加工和安装，在此一并感谢。同时感谢评审人对本文提出的宝贵意见。

附录A:

使用孔隙压力振荡法测量渗透率需要利用样品两端压力振幅比和相位差，下面给出孔隙压振荡法的微分方程以及振幅比α，相位差θ，无量纲参数Ψ和γ的求解方法。

孔隙压力振荡法的微分方程为

初始及边界条件为

其中，pd(t)和pu(t)所满足的关系如下

其中，P为样品中的压力，Pd为下游端压力，Pu为上游端压力，x为距下端面的长度，PA为产生的压力的振幅，L为样品的长度，A为样品的横截面积，k为样品的渗透率，η为孔隙流体的黏滞系数，βs为比储流率，Bd为下游端储流系数(Fischer et al.，1992)。由微分方程及边界条件得振幅比和相位差分别为

其中，κ=(βsπη/Tk)1/2显然从非线性方程求解太繁琐复杂，我们在实际操作过程中需要进行相应的预处理以及曲线分析并将结果代入计算。从所有的实验数据中截取稳定信号的数据，用于压力曲线的拟合以及相位差和振幅比的计算。因为测量出的下游振荡曲线，往往不是标准的正弦波，所以使用标准正弦曲线拟合的方法得到上下游压力曲线Pu=PAsin(ωt+δ)，Pd=αPAsin(ωt+δ+θ)，计算出振幅比和相位差并进行渗透率结果的迭代计算。对α和θ做如下变换:

将方程进行处理，使得振幅比α和参数γ能够用θ和Ψ来表示。

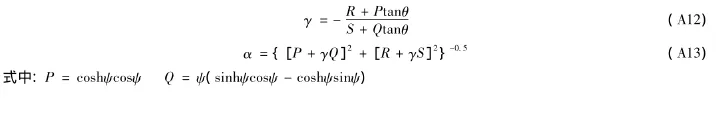
Ψ=L(πηβs/Tk)1/2，γ=Bd/(LAβs)均为无量纲参数。具体的计算步骤如下:

(1)相位差θ0和振幅比α0均为实验测量值，首先设定Ψ=0.1，且Ψ值的变化范围为0.1≤Ψ≤4.1，Ψ值的迭代步长为0.001;

(2)根据θ0和Ψ值初值(Ψ=0.1)，由公式(A12)可得γ0值，γ0值取正值;

(3)在公式(A13)中，由Ψ(0.1≤Ψ≤4.1，Ψ值的迭代步长为0.001)和γ0可求出α，将α与α0进行匹配，若︱α-α0︱＜0.05，则Ψ值可取，此时可得到多个Ψ值(假使有m个)满足方程(A13);

(4)同时根据α0和筛选出的Ψ值，由方程(A13)可反算出m个γ，根据筛选的Ψ和γ在方程(A12)中可反算出θ并与θ0做比较，若︱θ-θ0︱＜0.05，则Ψ和γ可取;

(5)Ψ=Ψ+0.001，重复上述(2)～(4)步骤;

将获得Ψ和γ代入公式，结合事先标定的下游端储流系数Bd求渗透率k和比储流率βs即可(Faulkner et al.，2000)。

陈颙，黄庭芳，刘恩儒.2009.岩石物理学［M］.合肥:中国科学技术大学出版社.

CHEN Yong，HUANG Ting-fang，LIU En-ru.2009.Rock Physics［M］.Press of University of Science and Technology of China，Hefei(in Chinese).

杨琼，聂孟喜，宋付权.2004.低渗透砂岩渗流启动压力梯度［J］.清华大学学报:自然科学版，44(12):1650—1652.

YANG Qiong，NIE Meng-xi，SONG Fu-quan.2004 Threshold pressure gradient of low permeability sandstone［J］.JTsinghua Univ(Sci＆ Tech)，44(12):1650—1652(in Chinese).

Al-Wardy W，Zimmerman RW.2004.Effective stress law for the permeability of clay-rich sandstones［J］.JGeophys Res，109(B4):B04203.

Bernabe Y，Brace WF，Evans B.1982.Permeability，porosity and pore geometry of hot-pressed calcite［J］.Mechanics of Materials，1(3):173—183.

Bernabe Y.1986.The effective pressure law for permeability in Chelmsford granite and Barre granite［J］.International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstracts，23(3):267—275.

Bernabe Y.1987.The effective pressure law for permeability during pore pressure and confining pressure cycling of several crystalline rocks［J］.JGeophys Res，92(B1):649—657.

Berryman JG.1992a.Exact effective-stress rules in rock mechanics［J］.Physical Review A，46(6):3307—3311.

Berryman JG.1992b.Effective stress for transport properties of inhomogeneous porous rock ［J］.JGeophys Res，97(B12):17409—17424.

Brace WF，Walsh JB，FrangoesWT.1968.Permeability of granite under high pressure［J］.JGeophys Res，73(6):2225—2236.

Brace WF.1980.Permeability of crystalline and argillaceous rocks［J］.International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstracts，17(5):241—251.

Cowan R D.1961.Proposedmethod ofmeasuring thermal diffusivity athigh temperatures［J］.Journal of Applied Physics，32(7):1363—1370.

Faulkner D R and Rutter E H.2000.Comparisons of water and argon permeability in natural clay-bearing fault gouge under high pressure at20℃ ［J］.JGeophys Res，105(B7):16415—16426.

Fischer G J.1992.The Determination of Permeability and Storage Capacity:Pore Pressure Oscillation Method［M］.Fault Mechanics and Transport Properties of Rocks，Chapter 8.Academic Press.

Fischer G J，Paterson M S.1992.Measurement of Permeability and Storage Capacity in Rocks during Deformation at High Temperature and Pressure［M］.Fault Mechanics and Transport Properties of Rocks，Chapter 9.Academic Press.

Ghabezloo S，Sulem J，Guedon S，et al.2009.Effective stress law for the permeability of a limestone ［J］.International Journal of Rock Mechanics and Mining Sciences，46(2):297—306.

Hsieh PA，Tracy JV，Neuzil CE，et al.1981.A transient laboratorymethod for determining the hydraulic properties of‘tight'rocks-Ⅰ.Theory［J］.International Journal of Rock Mechanics and Mining Sciences＆ Geomechanics Abstracts，18(3):245—252.

Kranz R L，Saltzman JS，Blacic JD.1990.Hydraulic diffusivitymeasurements on laboratory rock samples using an oscillating pore pressuremethod［J］.International Journal of Rock Mechanics and Mining Sciences＆ Geomechanics Abstracts，27(5):345—352.

Kwon O，Andreas K，Kronenberg，etal.2001.Permeability ofWilcox shale and its effective pressure law［J］.JGeophys Res，106(B9):19339—19353.

LiM，Bernabe Y，Xiao WⅠ，et al.2009.Effective pressure law for permeability of E-bei sandstones［J］.JGeophys Res，114(B7):B07205.

Morrow C A，Chong Z B，Byerlee JD.1986.Effective pressure law for permeability of Westerly granite under cyclic loading［J］.JGeophys Res，91(B3):3870—3876.

Neuzil C E，Cooley C，Silliman SE，etal.1981.A transient laboratorymethod for determining the hydraulic properties of‘tight'rocks-Ⅱ.Application［J］.International Journal of Rock Mechanics and Mining Sciences＆ Geomechanics Abstracts，18(3):253—258.

Nur A and Byerlee JD.1971.An exact effective stress law for elastic deformation of rock with fluids［J］.JGeophys Res，76(26):6414—6419.

Walsh JB.1981.Effect of pore pressure and confining pressure on fracture permeability ［J］.International Journal of Rock Mechanics and Mining Sciences ＆ Geomechanics Abstracts，18(5):429—435.

Warpinski N R，Teufel LW.1992.Determination of the effective-stress law for permeability and deformation in low-permeability rocks［J］.SPE formation evaluation，7(2):123—131.

Zhu W，Wong T F.1997.The transition from brittle faulting to cataclastic flow:Permeability evolution［J］.JGeophys Res，102(B2):3027—3041.

THE CALIBRATION OF ULTRALOWPERMEABILITY MEASUREMENT APPARATUS AND PRELIM INARY EXPERIMENTAL RESULTS

WU Man YANG Xiao-song CHEN Jian-ye
(State Key Laboratory of Earthquake Dynamics，Institute of Geology，China Earthquake Administration，Beijing 100029，China)

The low-ultralow permeabilitymeasurement is one of the most important research topics in fluid mechanics and rock physics.Quantification of fluid transport through fault zones is critical for the understanding of fault mechanics and prediction of subsurface fluid flow.In order to obtain the information about the fluid-flow processes in seismogenic regions，we have designed and constructed a distilled water/gas-medium permeability measurement apparatus capable of achieving ultralow permeability.The new measurement apparatus has used steady-state method and pore pressure oscillation method，which has become very popular recently because of its continuous measurement during processes that might alter the pore space of rocks and can measure samples with different permeabilitymagnitude fast and precisely，thus producing a basic environment in which the confining pressure reaches 200MPa by water，pore pressure reaches 40MPa either by water or gas at room temperature.In this paper，we have introduced some calibrating parameters in pore pressure oscillation method and given the experimental results on typical sandstones under seasonal cycle conditions.Our experimental results have showed that:(1)permeability by pore pressure oscillationmethod decreases with cyclic numbers slightly while permeability by steady state method decreasesmarkedly;(2)we have used empirical power law to fit the experimental values and the accuracy to pore pressure oscillation method is extremely high.We also have compared the results of the two differentmethods and found that pore pressure oscillation permeability is slightly larger than steady state permeability.Finally，we discussed the reasons that generate the discrepancy due to the method applied.Then we did some preliminary research on the pore pressure，and calculated effective pressure coefficent at intervals during the cycles.Large hysteresis in permeability has been observed，and effective pressure coefficient has been found to be loading path-dependent.At last，we used the least squaremethod on all experimental data to get the optimal effective pressure coefficient to make the best correlation between the permeability and the effective pressure.

permeability measurement，pore pressure oscillation method，steady-state method，effective pressure

P315.72+3

A

0253-4967(2011)03-0719-17

10.3969/j.issn.0253-4967.2011.03.020

2011-04-11收稿，2011-06-07改回。

国家科技专项汶川地震断裂带科学钻探(WFSD)09课题、地震动力学国家重点实验室自主研究课题(LED2010A03)和地震行业科研专项(2008419012)共同资助。

*通讯作者:杨晓松，研究员，E-mail:xsyang@ies.ac.cn。

吴曼，女，1985年生，中国地震局地质研究所构造地质学在读硕士研究生，现主要研究方向为高温高压岩石物理学，电话:010-62009030，E-mail:wudawoman1985@163.com。