基于层片分割算法的螺旋锥齿轮切削仿真

李敬财，李 琳，李 清，王太勇

(1. 天津大学机械工程学院，天津 300072；2. 天津石油职业技术学院机械工程系，天津 301607)

螺旋锥齿轮作为一种具有复杂曲面的零部件，由于其设计和加工过程很复杂[1-2]，往往需要对其切削过程进行仿真，以初步验证所使用的加工调整参数的合理性(如加工的齿顶是否变尖等)；此外可利用切削仿真得到的模型对其进行有限元分析或用于具有螺旋锥齿轮零件机械产品的装配模型中．

目前螺旋锥齿轮切削过程几何仿真主要通过以下两种方法实现．

(1) 依附于现有的商业软件实现切削过程几何仿真．基于现有的三维造型软件，通过二次开发进行加工切削过程的三维仿真，这种方法的速度较慢，很难或不能实现真正的实时仿真[3-4]；同时仿真过程不能脱离其二次开发的对应的三维造型软件，而这些软件通常都比较昂贵，往往会增加使用成本．

(2) 基于加工原理和啮合理论建立螺旋锥齿轮数学模型，在此基础上建立求解其齿面上的数据点，利用这些数据点得到螺旋锥齿轮的切削模型[5]．该方法有以下缺点：①需要建立复杂的螺旋锥齿轮的数学模型；②基于数学模型计算齿面数据点需要求解非线性方程组，求解过程极不稳定，尤其是碰到根切的情况不能计算出根切部分的齿坯加工情况；③计算过渡曲面和齿根曲面也不容易实现．

基于目前螺旋锥齿轮切削仿真存在的问题，笔者提出采用“层片切割” 切削仿真算法：通过将被加工零件进行适当的层片切割，在加工的每个时刻，利用刀具与被加工零件每个层片进行求交计算，并对相邻两时刻计算结果进行取舍，得到最终加工结果．本文以采用层片切割算法使用成形法加工小轮为例，说明该算法实现过程．

1 成形法小轮切齿坐标系的建立

图1所示为小轮切齿坐标系．xm2Om2zm2是与切齿机床固连的坐标系，x2O2z2是与齿坯固定的坐标系，xtOtzt是与刀具固连的坐标系．决定刀具安装位置的是水平轮位H2和垂直轮位V2，决定齿轮安装位置的是轴向轮位修正值ΔX2和安装角δM2，V2为正值时加工的是右旋齿轮，为负值时加工的是左旋齿轮．δM2、ΔX2、V2、H2均为加工小轮的机床调整参数．

图1 切齿坐标系Fig.1 Coordinates of gear cutting

2 切削刀具模型的建立

铣齿加工过程采用具有直线刃的铣刀盘来进行，(见图2)，每把刀具是由内刀和外刀组成，内刀和外刀绕刀具轴线旋转，分别形成了内锥面和外锥面，对应加工出螺旋锥齿轮的凸面和凹面，因此铣齿刀具内刀和外刀也可以分别看作为内锥面和外锥面．

在切削加工过程中刀具直线部分加工出齿轮啮合面部分，刀具的顶端切削刃加工出齿轮的根锥面．图3 为刀具顶端切削刃坐标系．图4 为刀具侧刃坐标系．

刀具顶刃径矢量rt1为

式中：Rw为刀具顶刃中点半径；u1为刀具顶刃上点距离中点距离值，正号表示该点在中点的右面，负号表示该点在中点左面；θ2为该点绕xt轴转角．

刀具侧刃径矢量rt2为

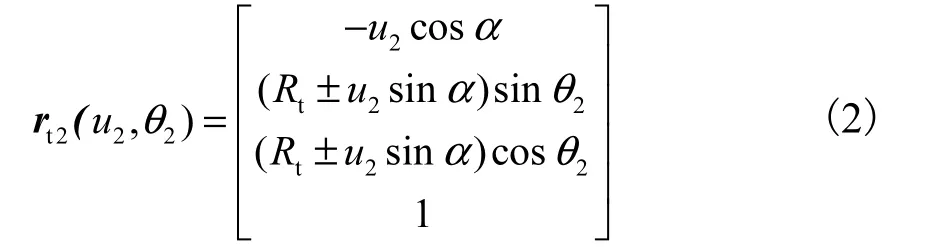
式中：负号表示内刀直线刃数学模型，正号表示外刀直线刃数学模型；α为压力角；Rt为刀尖半径；u2为内刀面或外刀面圆锥母线上的某一点距该母线上xt坐标为零的点的距离；θ2表示该点绕zt轴转角．刀具顶刃和侧刃在x2O2y2坐标系下，径矢量采用矩阵变换方式可表示为

图2 螺旋锥齿轮加工刀具Fig.2 Spiral bevel gears cutters

图3 刀具顶端切削刃Fig.3 Cutter tip edge

图4 刀具侧刃坐标系Fig.4 Coordinates of cutter side blade

式中V2前的正号表示加工右旋齿轮，负号表示加工左旋齿轮．

3 螺旋锥齿轮的层片分割

层片分割的目的是为了将被加工零件的坯料分割成有限相似的几何特征，该几何特征可与加工刀具进行求交运算．螺旋锥齿轮层片分割有如下2 个步骤：

(1)为求得刀具直线刃部分加工出的啮合面部分，先将螺旋锥齿轮齿坯分解为一系列的锥面(见图5)，然后在每个锥面上引出等间距的射线(见图6)，射线方程为

式中：αj为射线所在锥面的压力角；Rc为射线所在圆锥面的底面半径；u3为射线某一点距该射线上z2坐标为zi的点的距离；θj为射线与xt轴的夹角．

图5 锥面层片分割Fig.5 Slice cone

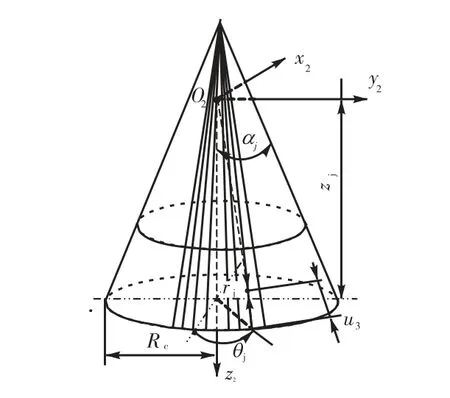
图6 锥面上射线Fig.6 Rays on cone surface

将刀具与引出的射线进行求交运算，所求交点为啮合齿面上的点(见图7)．

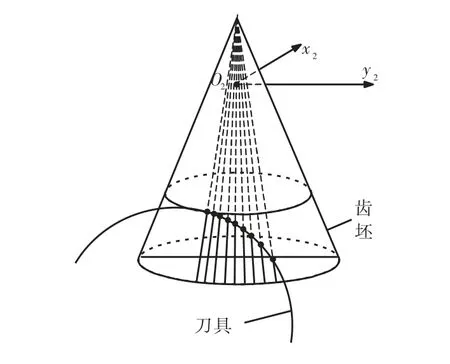
图7 刀具与射线交点Fig.7 Cross point between cutter and rays

(2)为求得刀具底刃加工出的齿底部分，可在根锥面上垂直引出一系列直线(见图8)，直线方程为

式中：R′c为根锥面的底面半径；u4为射线的长度；γm为跟锥角；θj′为射线与y2轴的夹角．

刀具底面与这些直线的交点为齿根面上的点，如图9 所示．

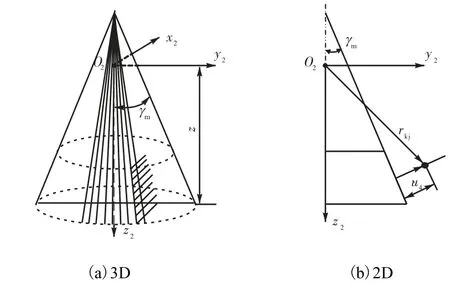
图8 垂直于锥面的射线Fig.8 Rays perpendicular to cone surface

图9 刀顶面与直线交点Fig.9 Cross point of cutter tip and line

4 切削过程求交计算及切削过程模型生成

切削过程求交目的是求得每一时刻刀具与毛坯相交的特征．求交的具体方法是通过求得刀具与层片分割后的毛坯对应的几何元素在每一时刻相交的特征(如点、线、面)，一般情况下为特征点，这些相交的特征便是刀具与毛坯相交特征的离散值．

在螺旋锥齿轮加工过程中，为求得每一时刻刀具与毛坯相交时的啮合面特征，需要计算出齿坯的所有分割锥面上的直线族与刀具侧刃的交点(图7)，求交公式为由式(4)和式(8)联立的方程组；为求得每一时刻刀具与齿坯相交的齿根面特征，需要计算出刀具底部切削刃与所有引出直线的交点(图9)，求交公式为由式(3)和式(9)联立的方程组．

通过以上计算可得到螺旋锥齿轮的齿面离散点，如图10 所示，得到的螺旋锥齿轮切齿仿真模型如图11 和图12 所示．

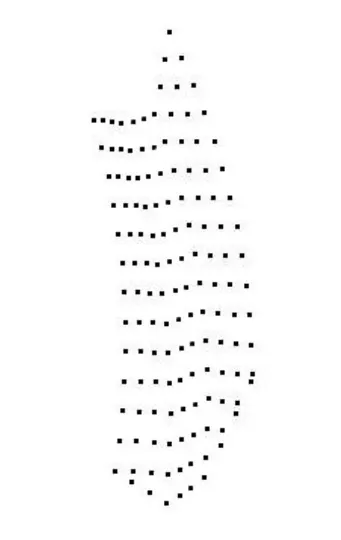
图10 构成齿面的点Fig.10 Points of tooth surface

图11 齿面模型Fig.11 Model of tooth surface

图12 齿轮模型Fig.12 Gear model

5 结果验证

本文中给出了采用层片分割算法计算出刀倾法加工小轮切齿仿真模型的实际算例．表1 为准双曲面齿轮小轮齿坯数据；表2 为小轮机床调整参数；表3 为求交所得数据与理论值的比较．对比结果表明，层片分割算法计算结果准确、方法可行．

表1 小轮齿坯数据Tab.1 Blank data of pinion

表2 小轮机床调整参数Tab.2 Machine settings of pinion

表3 小轮计算结果Tab.3 Calculating results of pinion

6 结 语

将层片分割算法应用在螺旋锥齿轮的切削仿真中，成功解决了以往螺旋锥齿轮切削仿真存在仿真速度慢、不能脱离现有商业软件的问题；此外，由于采用层片分割算法计算出的齿面精度很高，因此该模型可用于对螺旋锥齿轮的后续分析，例如对螺旋锥齿轮的有限元分析、齿面接触分析(tooth contact analysis，TCA)及有载接触分析(load tooth contact analysis，LTCA)．值得一提的是该算法也可以应用到其他零件的切削仿真中．

［1］董学朱. 齿轮啮合理论基础[M]. 北京：机械工业出版社，1989.Dong Xuezhu.Gear Meshing Theory[M]. Beijing：China Machine Press，1989(in Chinese).

［2］曾 韬. 螺旋锥齿轮设计与加工[M]. 哈尔滨：哈尔滨工业大学出版社，1989.Zeng Tao.Design and Manufacture of Spiral Bevel Gear[M]. Harbin：Harbin Polytechnical University，1989(in Chinese).

［3］Litivin F L.Gear Geometry and Applied Theory[M].New Jersey：PrenticeHall，1994.

［4］熊越东，王太勇，张 威. 螺旋锥齿轮数控加工三维仿真研究[J]. 制造业自动化，2005，27(6)：21-23.Xiong Yuedong，Wang Taiyong，Zhang Wei. Research on NC machining 3D simulation of spiral bevel and hypoid gears[J].Manufacturing Automation， 2005 ，27(6)：21-23(in Chinese).

［5］熊越东，王太勇，刘富凯. 准双曲面齿轮数控加工仿真系统设计[J]. 组合机床与自动化加工技术，2005(7)：43-45.Xiong Yuedong，Wang Taiyong，Liu Fukai. Design on NC machining simulation system of hypoid gears[J].Modular Machine Tool and Automatic Manufacturing Technique，2005(7)：43-45(in Chinese).