基于三角形剖分算法建立三维巷道模型的研究
2011-12-06蔡美峰李角群杨志军
蔡美峰,李角群,杨志军
(北京科技大学土木与环境工程学院,北京100083)
对于地下矿山工程项目,无论是在矿山设计阶段或是生产过程中,建立矿工程三维实体模型具有重要意义[1-3]。在设计阶段,该模型往往配合矿体三维实体模型及地表三维模型,直观的反映设计意图和思想,完整表达各种模型的空间关系,可以及时发现设计中出现的空间位置的错误。在生产中,准确的采矿工程三维实体模型的建立,不但给管理人员带来直观显示,同时也是设计人员进行采矿设计的重要依据[4]。例如:中深孔爆破是矿山生产中重要环节,其爆破质量对生产有很大影响,爆孔过深或者过浅都直接影响爆破质量。中深孔爆破设计的优劣主要取决于测量的准确程度。通过建立采矿工程三维实体模型,可以进行准确的切剖,可保证中深孔爆破设计质量[5-6]。
1 三角剖分算法的基本概念
三角剖分算法包含如下几个基本概念:1)“网体”与“实体”
在ACAD中的三维“实体”,与一些矿业软件(如 SURPAC、DA TAM INE等软件)中的“实体”是不同的两个含义。前者是基于ACIS建立的实体,后者是一种由大量三角面围成的闭合体。后者在ACAD中称呼为“网体”。
2)“网体”转换“实体”
在ACAD中,三维“实体”可以任意切剖,也可进行实体布尔 (交、并、差)运算。但实体建立方法还不能满足矿山各种模型建立的需求。“网体”建模比较灵活方便。但ACAD中并没有提供“网体”转换“实体”的功能。笔者经过多年研究,找到了“网体”转换“实体”的方法,实现了网体转换实体功能。
3)带约束的三角剖分
如何把一个散点集合剖分成不均匀的三角形网格,这就是散点集的三角剖分问题。目前,三角剖分以Delaunay法的应用最为广泛。带约束的三角剖分,则是有各种约束边 (如内、外边界线,等高线等),每个约束边必是三角形的边。其算法是在无约束三角网剖分基础上,逐个插入约束边,将与约束边相交的三角形删除,形成空区的边界点与约束边,重新进行三角形剖分,确保约束边是三角形的一条边。
4)扩展数据
扩展数据是一组可以与图元几何内容无关的数据,在ACAD中有个很有价值的功能,几乎所有图元都支持扩展数据的存储。此功能解决了三个问题:第一,图元属性问题;第二,图元关联问题;第三,数据存储问题。本文中主要采用该格式进行数据存储。
在设计阶段,完全可以采用拉伸或放样功能实现采矿工程三维实体模型建立。本文重点介绍矿山生产过程中,如何在实测基础上建立巷道三维实体模型。在矿山生产中,巷道实测数据是通过支距法测量得到的,但由于矿山往往没有相应的程序模块,实测数据没有进一步规范整理与计算,只是辅助技术人员将巷道平面轮廓线绘制到平面图中,效率非常底,且丢失顶底板标高数据,使实测巷道数据缺失,仅由巷道轮廓腰线来反映实测巷道。针对测量数据完整与测量数据缺失两种情况,采用了两种不同的建模方法。
2 基于测量数据完整的巷道三维实体模型的建立
2.1 三维实体模型的建模步骤
对于新施工进行测量验收的巷道,其实测数据是完整的。对于实测数据结果,巷道三维模型的建模的基本步骤:
1)实测数据的整理与计算:通过 EXCEL电子表格进行测量数据的规范整理,在EXCEL中调用基于VB编写的模块完成自动计算;
2)巷道的平面展图绘制:在ACAD中调用程序读取EXCEL中的计算结果,在平面图中自动进行巷道的平面展图绘制;
3)巷道封闭曲面的构筑:通过巷道导线的选取,自动构筑巷道封闭曲面,建立巷道三维实体模型。
2.2 测量数据的整理与计算
巷道测量数据的整理和计算非常重要,它不但规范了数据电子化存储,也提高了平面实测巷道图绘制的效率。根据支距法的特点,在 EXCEL中,设计了给法空表格的自动绘制,将实测数据录入到表格后,调用计算程序模块完成测量的自动计算。计算结果如表1所示。
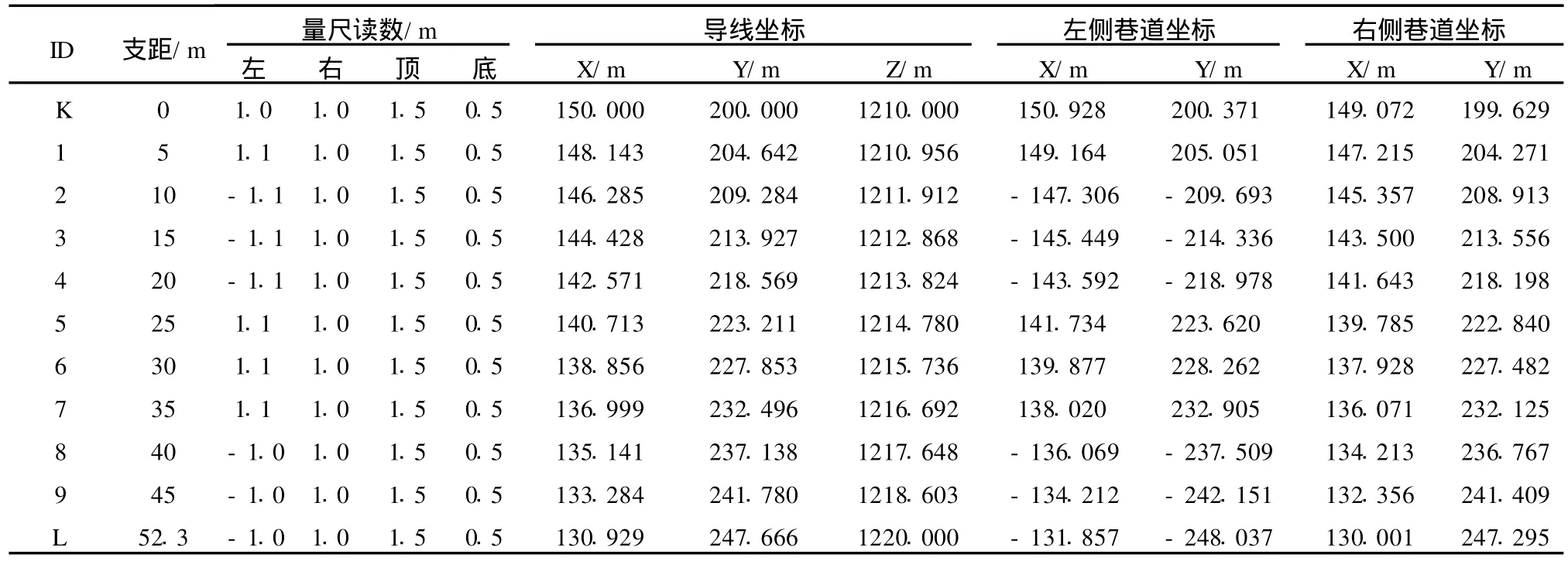
表1 支距法测量记录计算表
通过计算,巷道的导线及左右腰线的坐标都自动填写在表格中,为巷道的平面图及三维实体模型生成做准备。
2.3 巷道的平面展图绘制
由于平面展图的坐标数据都已经在计算表中,通过调用程序读取表格 (表1),可以自动进行巷道平面展图绘制。主要方法是:将表格中各点左右顶底数据,以扩展数据的形式记录在巷道的导线中,为巷道的三维实体模型生成做准备,巷道平面示例如图1所示。
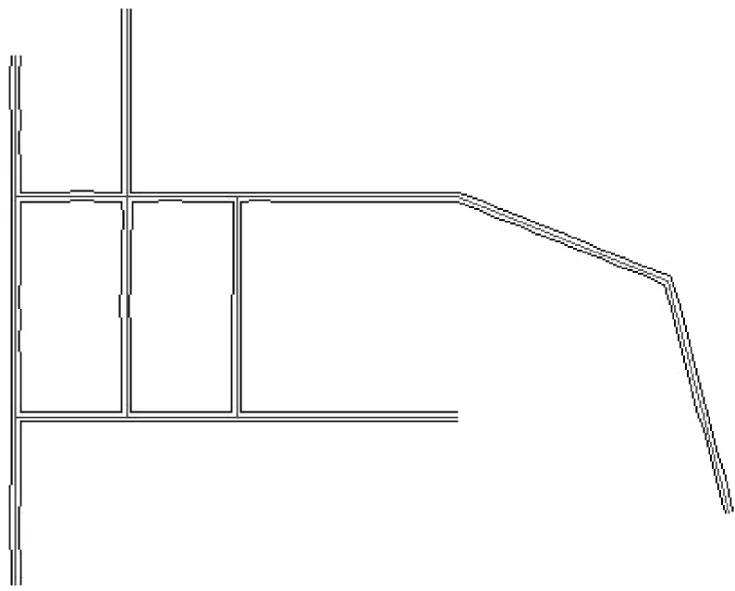
图1 实测巷道平面展图
2.4 巷道封闭曲面的构筑
经分析可知,巷道封闭曲面主要由两部分组成:一种是沿走向的侧面,由两两边线三角剖分组成;一种是两个端面,分别由一条闭合线三角剖分组成。
1)两条对应线三角剖分示意,如图2所示。

图2 两条对应线三角剖分示意图
边线a与边线b对应,三角剖分方式如图2所示。如果线有 n个点组成,分别取线a的 (a1,a2)、(a2,a3) ……. (an-1,an)与线b的 b1、b2……bn-1组成三角形,再分别取线 b的 (b1,b2)、(b2,b3) ……. (bn-1,bn)与线a的a2、a3……an组成三角形,完成最终剖分。
2)一条闭合线三角剖分示意,如图3、图4所示。
以矩形和1/3三心拱为例。矩形最为简单,剖分2个不交差或重叠三角形即可。三心拱共剖分5个三角形,剖分位置如图所示。三心拱图中的1、4、7三点的坐标比较容易计算出,顶底差 (巷道净高)包括了墙高和拱高。在实际矿山应用中,往往假定墙高不变,拱高是变化的。据此假设,2、6两点也很容易求得,3、5两点的坐标根据式(1)、式 (2)计算,3、5两点相对于2点变化增量 Dx,Dy分别为:
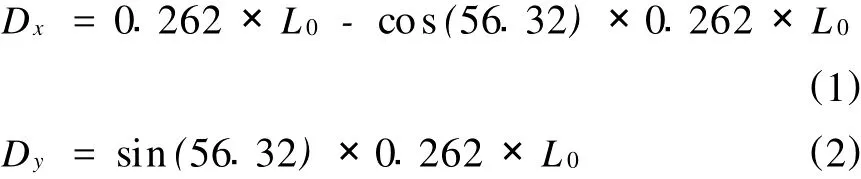
式中L0为巷道实测净宽。
如前所述,巷道的实测数据都已经保存在巷道导线中,对于不同巷道断面,巷道封闭曲面的构筑也不相同。对于矩形巷道最为简单,见图5和图6。
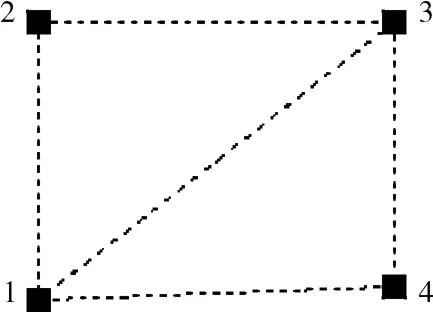
图3 矩形三角剖分示意图
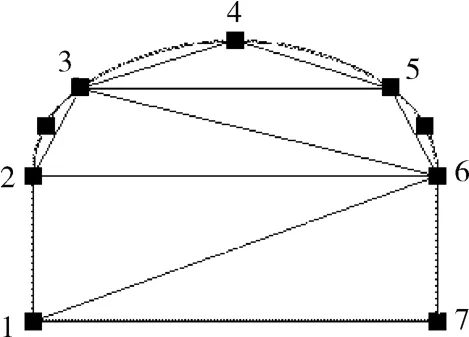
图4 三心拱三角剖分示意图
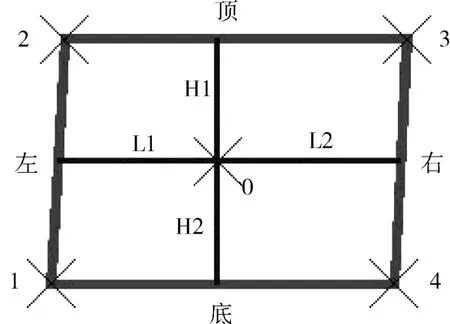
图5 矩形巷道边线算法
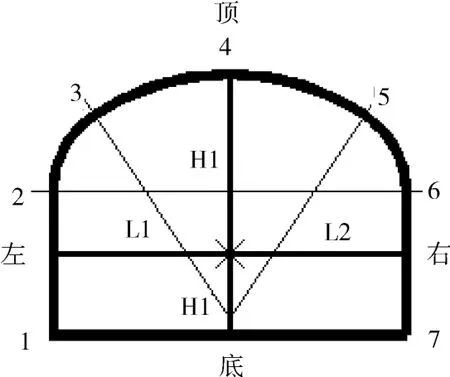
图6 三心拱巷道边线算法
由以上计算方法,矩形断面边线坐标计算如下:
边线1:x1=x0-L1;y1=y0-H2
边线2:x2=x0-L1;y2=y0+H1
边线3:x3=x0+L2;y3=y0-H2
边线4:x4=x0+L2;y4=y0+H1
三心拱断面边线坐标计算如下:
边线1:x1=x0-L1;y1=y0-H2
边线2:x2=x0-L1;y2=y0+H-H2
边线3:x3=x0-L2+Dx;y3=y0+H-H2+Dy
边线4:x4=x0;y4=y0+H1
边线5:x1=x0+L2-Dx;y1=y0+H-H2+Dy
边线6:x2=x0+L2;y2=y0+H-H2
边线7:x7=x0+L2;y7=y0-H2
其中:H为墙高;Dx,Dy同上。
由此,可以求出巷道的各个边线,按两条对应线三角剖分方法,可以完成巷道侧面剖分,从而完成巷道封闭曲面的构筑。再通过“网体”转换“实体”功能模块,即可完成巷道三维实体模型的建立。三维巷道模型见图7。

图7 巷道三维实体模型图
3 基于测量数据缺失的巷道三维实体模型的建立
3.1 三维实体模型的建模步骤
目前,大多数生产矿山没有实测数据整理和计算程序模块。虽然有实测巷道的平面展图,但巷道的顶底板标高数据还是缺失的,仅由巷道轮廓腰线来反映实测巷道。对此种情况,建模过程为:
1)对巷道轮廓腰线进行有约束的三角剖分;
2)根据剖分的三角形自动构筑巷道封闭曲面;3)建立巷道三维实体模型。
3.2 巷道轮廓腰线的带约束三角剖分
首先,对平面图中巷道轮廓腰线进行必要的处理,内外边界都连接成各自的闭合线。然后,采用VB编写的带约束的三角剖分程序进行三角形剖分。三角剖分结果见图8。
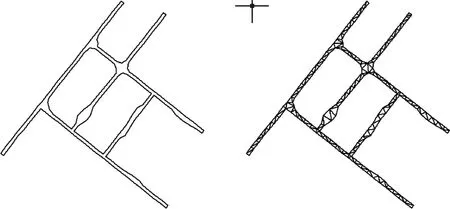
图8 巷道带约束的三角剖分图
3.3 巷道封闭曲面的构筑
对于矩形断面巷道,巷道封闭曲面的构筑比较简单。首先,将已剖分三角形做为底面,完全复制并相对向上移动到一个巷道高的位置后,完成了巷道顶面的构筑。然后,同样对每个内外边界进行复制并相对向上移动到一个巷道高的位置后,每个边界与其复制的边界进行两条对应边的三角剖分,完成巷道侧面的构筑。到此完成了矩形巷道封闭曲面的构筑。
对于三心拱 (圆弧、半圆)断面巷道,巷道封闭曲面的构筑比较复杂。巷道底面与侧面的构筑与矩形相同,关键在于顶面的形成。顶面不是简单的复制,由于有拱高的存在,需要将顶面三角形进行二次碎分。经过分析可以看出,顶面三角形分三种类型,如图9所示。
第1种类型:三角形的3个顶点,在某边线上是连续拐点,它通常在巷道的端头。
第2种类型:三角形的3个顶点中的2个顶点,在某边线上是连续拐点,它在巷道的正常段。
第3种类型:三角形的3个顶点,对任何边线都没有连续性,它在巷道的交叉位置。
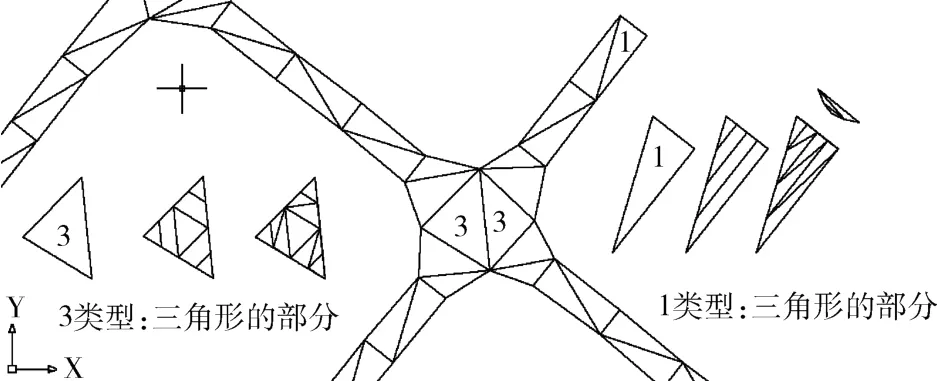
图9 巷道顶面三角形碎分图
具体碎分过程如下:首先,对所有三角形进行分类,图9中三角形除了类型标注的外,都属于第2种类型。然后,对不同类型进行不同的碎分。
针对第1种类型:需要进一步判断哪个边是端头,方法可以使用夹角去判断,巷道端边与壁边的夹角往往趋近90°。确定端边与壁边后,将端边4等分,并平行于壁边将三角形分成4个区域,其中一个是三角形,另外3个是四边形,将四边形再分成2个三角形,完成了1类型三角形的顶面碎分。对于端边,计算出4等份位置在端部的高程点,将拱碎分成3个三角形,顶部1个,下面梯形再碎分成2个。至此,完成了第1种类型三角形碎分。
针对第2种类型:与第1种类型的顶面碎分相同。
针对第3种类型:将每个边进行4等份,如图9所示将三角形碎分成4个三角形和3个梯形,再将每个梯形分成2个三角形。至此,完成了第3种类型三角形碎分。
需要说明的是,一般都假设墙高 H不变。如果底板标高为 E,则顶面三角形3个顶点的标高为E+H。由实测数据可知,巷道净宽L0和净高 H0是变化的,即拱是变化的,顶面三角形碎分中都进行了4等份,其中,中间点的标高为 E+H0,两侧点的标高根据巷道断面类型不同,参照设计手册将有不同的计算公式。以1/3三心拱断面为例,两侧点的标高为 (E+H0)-0.695×L0+
至此,完成了巷道封闭曲面的构筑。再通过“网体”转换“实体”功能模块,最终完成巷道三维实体模型的建立,见图10。
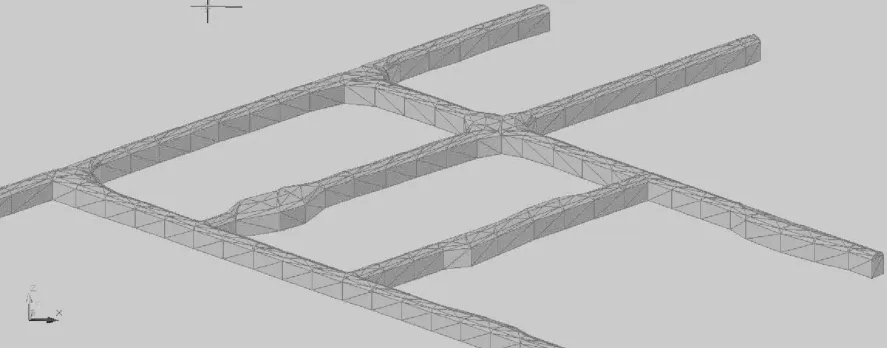
图10 巷道三维实体模型图
4 结论
矿山巷道三维实体模型的建立,对矿山生产设计和管理有重要意义。本文分别针对具有完整测量数据和缺少测量数据的两种情况,建立了巷道三维实体模型。主要得出以下结论:
1)在具有完整的实测数据前提下,运用三角剖分法将二维的网体转换为巷道的三维实体,使得矿山巷道更具实用及直观性。
2)在缺少完整实测的数据前提下,运用带约束的三角剖分算法,在碎分的基础上构筑了巷道的封闭曲面,通过VB编译模块将网体转换实体,建立了巷道的三维实体图。
3)巷道的三维实体模型的三角剖分算法,进一步完善了现有矿山巷道三维实体模型的建立的手段,有很强的实用性,为矿山中深孔设计提供较大的方便。
[1] 杨奎奇,潭海樵.面向对象的巷道三维显示与查询系统模型 [J].煤矿现代化,2004,58(1):35-36.
[2] 汪云甲,伏永明.矿井巷道三维自动建模方法研究 [J].武汉大学学报 (信息科学版),2006,31(12):1097-1100.
[3] 吴立新.数字地球、数字中国与数字矿区 [J].矿山测量,2000(1):6-9.
[4] 孙中昶,卢秀山,田茂义.矿山巷道3维建模算法研究及实现 [J].测绘学报,2009,38(3):250-254.
[5] 王建民.三维巷道建模及其应用研究 [D].太原:太原理工大学,2005.
[6] 梁建斌,张和生.应用OpenGL进行巷道三维显示研究[J].太原理工大学学报,2006,37(2):142-145.
