考虑因子交互作用多目标优化注塑模冷却系统工艺参数
2011-12-04舒茂盛毛华杰
舒茂盛,兰 箭,毛华杰,尹 飞
(武汉理工大学材料科学与工程学院,湖北武汉430070)
考虑因子交互作用多目标优化注塑模冷却系统工艺参数
舒茂盛,兰 箭,毛华杰,尹 飞
(武汉理工大学材料科学与工程学院,湖北武汉430070)
运用部分因子实验设计方法从众多的实验因子中初步筛选出与注塑模冷却系统密切相关的若干个独立因子和交互因子。在考虑交互因子的基础上,结合Taguchi试验设计和模糊数学中的综合评判法,对成型周期和冷却结束时型腔温度差2个目标值进行综合评判,得到综合评分;通过对综合评分进行极差分析,确定了各工艺参数对综合评分的影响程度,从而获得了优化的工艺参数组合。
注塑模;冷却系统;工艺参数;多目标优化;Taguchi试验设计;交互作用
0 前言
完整的注射成型过程包括填充、保压和冷却3个阶段,其中,塑料制品在型腔中的冷却时间占整个成型周期的80%左右。长期以来,注塑模冷却系统的设计及工艺参数的确定主要依靠设计者的经验和直觉,缺乏理论依据和科学计算,往往导致模具成型周期过长,并可能导致产品冷却不均而产生质量问题。
近年来,对注塑模具冷却系统的优化设计主要通过边界元温度场合灵敏度分析为基础,或将算法与CAE技术结合,对冷却系统优化设计。Lam等[1]综合考虑冷却系统布局及冷却参数的选择,以型腔表面的温度均匀分布为目标,将演化算法和CAE技术相结合,确定出合适的冷却系统;Lin[2]利用 CAE模拟技术、模糊神经网络和模拟退火算法,以实现塑件最小翘曲为目标,来确定冷却管道的位置参数。但是,人们依靠经验选取数量较少的实验因子来考察单个因子对实验目标的影响,进而优化目标,忽略了因子之间交互作用对实验目标的影响。另外,学者只是对实现均匀冷却或者制件最小翘曲变形等单一目标对冷却系统进行优化,制件很难在较短时间内实现均匀冷却。本文即在此前提下对影响冷却系统实验因子的选取和因子交互作用做了尝试性的研究,将交互因子计入重要影响参数组织实验来优化目标,为了使成型周期较短和型腔冷却均匀,利用模糊数学的综合评判法,根据目标值对生产效率、产品质量等方面影响重要程度,进行加权综合评分,然后通过极差分析,确定各因素对综合值的影响程度,从而获得优化的工艺参数组合。
1 部分因子实验设计方法
影响冷却系统的因素很多,除了塑料制品的几何形状、冷却水路的布置、冷却介质流量和温度、模具材料、塑料熔体温度、模具温度、顶出温度外,还涉及到塑料与模具之间的非稳态热循环交互作用。这些参数不但以单个因子的作用方式影响着冷却系统,而且它们之间还存在着非常复杂的交互作用。部分实验因子设计方法是一种考虑因子两两交互作用而设计的实验方法,能够用较少的实验从众多的输入变量中筛选出影响制件质量的关键因子和重要交互因子[4],部分因子实验所需要的实验次数如(1)所示:

式中N——部分因子实验次数
k——实验因子个数
n——实验水平
m1——实验重复次数
q——部分收缩度,随着q的增加实验次数降低
该实验方法的特点是只选择代表性很强的实验;能够考察每个因子及因子交互作用对质量指标的影响程度,并进行排序选出重要的实验因子,从而对实验因子有效性的选择提供了可靠的依据。
1.1 参数和优化指标的确定
本文选用的模型是一个复印机零部件,如图1所示。材料为德赛化学工业有限公司生产的聚碳酸酯(PC)+丙烯腈-丁二烯-苯乙烯(ABS),牌号为 Novalloy S 1100。影响冷却系统的因素有很多,选择冷却过程所有的工艺参数作为考察因子,具体的实验因素和因素水平如表1所示,选用正交表L8(25)在Moldflow中进行实验。

图1 试验模型Fig.1 The experiment model
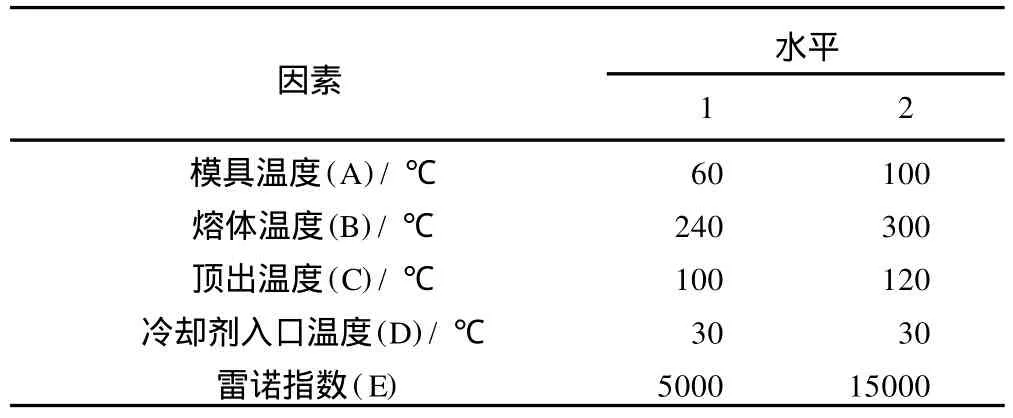
表1 试验因素及水平Tab.1 Factors and levels in the screening design
衡量模具冷却质量的标准有2个:一是成型周期短;二是使型腔各部位均匀冷却。分析的目标是确定成型周期(Y1)和型腔温度差(Y2)的综合评分值。为保证产品生产效率和使用要求,成型周期和型腔温度差必须满足以下条件:19.2 s≤Y1≤29.8 s;0≤Y2≤40℃。
1.2 交互作用分析
在交互实验中,2个因子与实验目标值的关系可以用交互作用图来表示(如图2所示),根据因子交互作用关系图,可以判断实验因子之间是否存在交互关系。当横坐标的一个实验因子从低水平过渡到高水平时,该因子对目标值的影响度随着另外一个因子在其实验范围内有较大改变,即它们对目标值的影响曲线不平行,则两因子之间存在交互作用[5]。由图2可以看出,对成型周期和型腔温度差同时存在影响的有4个明显的交互作用:
(1)模具温度对雷诺指数(AE)。在较低模具温度下,成型周期随着雷诺指数的升高而增加;相反,在较高模具温度下,成型周期随着雷诺指数的升高而降低;而两者对型腔温度差的影响趋势刚好相反;
(2)冷却剂入口温度对雷诺指数(DE)。在较低冷却剂入口温度下,成型周期随着雷诺指数升高而减少;相反,在较高冷却剂入口温度下,成型周期随着冷却剂入口温度的升高而增加;而两者对型腔温度差的影响趋势相反;两者交互作用都明显;
(3)顶出温度对冷却剂入口温度(CD)。在较低顶出温度下,成型周期随着冷却剂入口温度的升高而增加;相反,在较高顶出温度下,成型周期随着冷却剂入口温度的升高而降低;而两者对型腔温度差的影响趋势相同,且较明显;
(4)顶出温度对雷诺指数(CE)。在较低顶出温度下,成型周期随着雷诺指数的升高而增加;相反,在较高顶出温度下,成型周期随着冷却剂温度的升高而降低;而两者对型腔温度差的影响趋势相同;两者交互作用都明显。
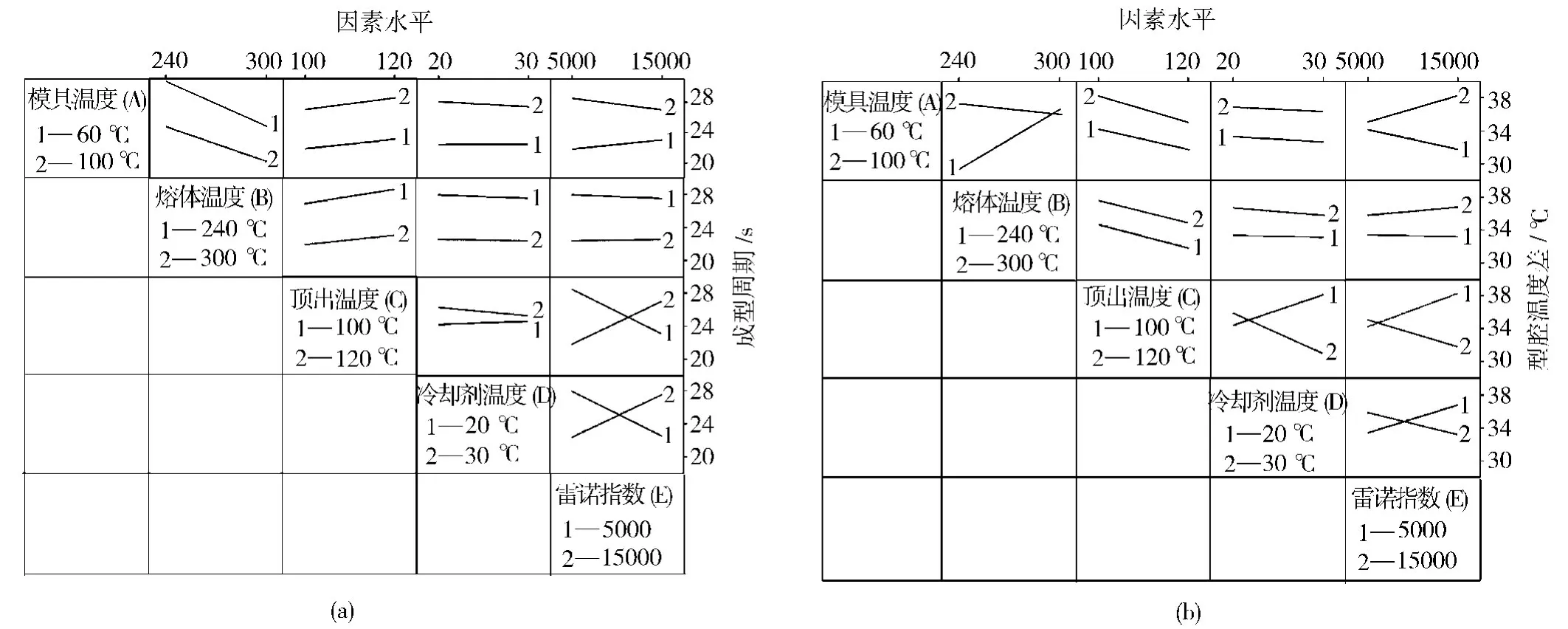
图2 工艺参数对成型周期和型腔温度差的交互作用图Fig.2 Interaction plot for cycling time and cavity temperature difference
1.3 各实验参数对目标值的影响度
部分因子实验设计通过分析主效应和交互效应对目标值的相对贡献来筛选主要因子及主要交互作用因子。计算公式如式(2)、(3)所示:

式中Ej——第j个因子对实验目标的主效应
Ijk——第j个因子与第k个因子的交互效应
n——实验总次数
i——实验序号
j、k——实验因子序号
m——实验因子总数
Ri——第i次实验的目标值
其中,lij=±1,当第i次实验的第j个因子处于低水平时等于-1,处于高水平时等于1,且n次实验lij总和等于零。
应用式(2)、(3)分别可以计算出单个因子和因子间交互作用对目标值的影响程度。
效应值的绝对值反应了因子对目标值的影响程度,从而选出主要的单个因子和交互作用因子,为后续工艺优化提供依据。从图3可以看出,单个因子模具温度(A)、熔体温度(B)、顶出温度(C)和冷却剂入口温度(D)对2个目标值影响比较大,雷诺指数(E)本身对2个目标值的影响不大,可以忽略不计,但是雷诺指数对模具温度(AE)、对冷却剂入口温度(DE)存在交互作用。从图3(b)可以看出,雷诺指数和冷却剂入口温度(DE)对目标值的影响甚至超过了冷却剂入口温度(D),因此,有必要将AE和DE作为重要的实验因子之一。

图3 各因子及交互作用对成型周期和型腔温度差的效应图Fig.3 Main effect plot of factors and interactions for cycling time and cavity temperature difference
2 冷却系统工艺优化设计
2.1 Taguchi实验设计
注塑工艺是一个复杂的过程,影响制件的工艺参数很多,为了减少试验次数,同时获得足够的参数,模拟试验采用 Taguchi实验设计理论,该理论最突出的特点是只用较少的试验次数就可以由试验结果通过计算推断出最优的参数组合。具体实验因素及水平设计如表2所示。

表2 试验因素及水平Tab.2 Factors and levels in the Taguchi design
由部分因子实验设计可知,有2对因子交互作用是影响目标值的重要因子,必须将这些交互影响也作为实验因子安排在正交实验表中,重新进行实验以获取更准确的结果。本文采用正交矩阵L27313(如表3所示)。将交互因子DE安排到3、4两列,交互因子AE安排到6、7列,其他因子的安排如正交矩阵所示,其中e表示误差,对应的目标值也列在表3中。

表3 正交表及试验结果Tab.3 The orthogonal array and result of this study
模拟试验所选取的目标值对注塑模冷却系统的影响程度各有侧重,因此,有必要建立一个使各个目标值都尽可能好的综合评判方法,从而将多目标问题转化为单目标,实现多目标问题的综合优化。权值分配根据各目标值对冷却系统综合质量的影响程度,按百分制加权,因为均匀的型腔温度有利于缩短成型周期,所以将成型周期和型腔温度差的权值定为b1=20,b2=80。加权综合评分值Yj的计算公式[6]如式(4)所示:
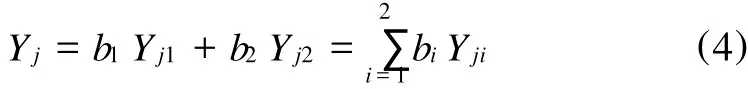
式中j——实验序号
Yj——第j个实验的综合评分
由于成型周期和型腔温度差的量纲不同,因此有必要将两者统一映射到[0,1]的数值空间中。根据各目标的约束条件,采用模糊数学中的S形分布映射函数来实现对各目标的映射,函数如式(5)所示。
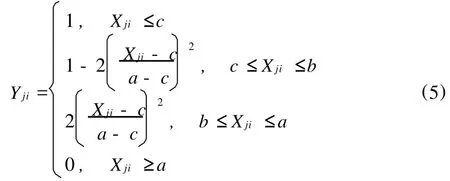
式中i——目标指标(成型周期和型腔温度差的i分别为1,2)
Yji——第j个实验的第i个目标的映射
Xji——第j个实验的第i个目标的实验结果
a、b、c取值如表4所示。综合评分结果如表3所示。
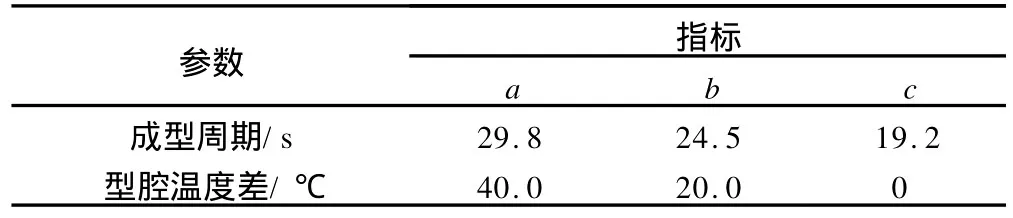
表1 函数参数取值Tab.1 Parameter of function
2.2 结果分析
为了得出各因素与综合指标间的关系,找到各因素对综合指标影响的规律,从而得到各因素水平的最佳组合,模拟实验采用极差法对数据进行分析。极差是指一组数据中最大值和最小值之差,极差值越大,表示该因素对指标的影响程度越大,该因素越关键;极差值越小,表示影响程度越不显著,因素重要程度越一般。模拟实验中各因素的极差值如表5所示。

表5 综合评分极差分析结果Tab.5 The range analysis result of comprehensive evaluation
根据极差分析,由图4可以直观地看出,工艺参数对综合指标的影响程度排序为:熔体温度(B)>顶出温度(C)>模具温度(A)>雷诺指数(E)>冷却剂温度(D)。图4中各因素水平的综合评分值越高,所组成的工艺方案越好,可以得出该模型的最佳因素水平组合是A1B1C3D3E1。通过Moldflow分析验证,模拟实验结果为:最大冷却时间为20.34 s,型腔温度差31.1℃,综合评分值为27.46,该值高于表3中的任一组合的综合评分,证明该方案为最佳工艺组合方案。

图4 各因素水平影响趋势图Fig.4 Influence plot of factors and its levels
3 结论
(1)采用部分实验因子设计方法,用尽可能少的实验从众多的实验因子中筛选出与实验目标值密切相关的重要因子和交互作用因子,为后续的实验安排提供可靠依据;
(2)结合 Taguchi试验设计和模糊数学综合评判法,通过对影响冷却系统优化设计的2个目标值进行综合评价,采用极差分析获得最佳工艺组合,从而优化了冷却系统工艺参数;
(3)当冷却介质处于紊流状态(Re>4000),雷诺指数自身的改变对实验目标值影响较弱,可以忽略不计;但是与模具温度和冷却剂入口温度的交互作用对目标值影响较强,甚至超过了冷却剂入口温度本身对实验目标的影响。
[1] Lin Y C,Zhai L Y,Tai K.An Evolutionary Approach for Cooling System Optimization in Plastic Injection Moulding[J].International Journal of Production Research,2004,42(10):2047-2061.
[2] Lin J C.Optimum Cooling System Design of a Free-form Injection Mold Using an Abductive Network[J].Journal of Materials Processing Technology,2002,120:226-236.
[3] 张志莲,江 波.注塑成型工艺参数间的交互作用[J].化工学报,2006,57(2):448-452.
[4] Keun Park,Jong Ho Ahn.Design of Experiment Considering Two-way Interactions and It Application to Injection Molding Processed with Numerical Analysis[J].Journal of Materials Processing Technology,2004,146:221-227.
[5] 张志莲,江 波.考虑因子交互作用优化注射成型工艺参数[J].高分子科学与工程,2006,22(2):30-34.
[6] 潘柏松,龚惠玲,刘 红.基于正交试验法的注塑工艺多目标优化设计[J].浙江工业大学学报,2007,35(3):308-312.
Multi-objective Optimization Design of Processing Parameters of Injection Molding Cooling System Considering the Interactions
SHU Maosheng,LAN Jian,MAO Huajie,YIN Fei
(School of Materials Science and Engineering,Wuhan University of Technology,Wuhan 430070,China)
A fractional factorial experiment was employed to screen out significantly independent and interactive factors among numerous processing parameters that are closely related to injection molding cooling system.And,regarding the interaction effect,the cycling time and cavity temperature difference at the end of cooling were taken as the optimization objectives to evaluate their contributions using Taguchi experiment design method as well as with fuzzy comprehensive judgment method.Through an analysis of the evaluation,the influence of various process parameters was clarified,and an optimum combination of processing parameters was thus determined.
injection molding;cooling system;processing parameter;multi-objective optimization;Taguchi experiment design;interaction
TQ320.66+2
B
1001-9278(2011)06-0065-05
2010-12-30
联系人,sms0209@126.com
