钢管塔十字节点板强度理论与试验研究

邓洪洲，黄 誉

（同济大学 建筑工程系，上海200092）

插板连接具有能自由调整节点板尺寸，连接简单，易于保证施工质量等优点而广泛用于输电钢管塔结构中.常见型式有单插板连接和U 插板连接.单插板连接主要用于受力较小的杆件连接；受力较大的杆件通常采用U 插板连接（图1a）.单插板和U 插板侧向刚度小，且U 插板连接对现场安装精度要求较高.本文研究的十字插板连接弥补了传统插板的缺点，安装方便，同时其侧向刚度大，整体性能好，尤适用于大型钢管塔架结构的节点连接，值得推广应用.日本某1 000kV输电线路就采用了这种十字插板连接（图1b）.

与普通单插板、U 插板相对应的是传统节点板.国内外相关学者对传统节点板的受力性能进行了大量的试验和理论研究，具有开创意义的是Whitmore对铝节点板进行的力学性能试验，根据试验结果，提出了著名的有效宽度法来验算节点板强度［1］.Hardash等进行了28个节点板的静力试验，提出了节点板块体剪切破坏模型［2］.Yamamoto等进行了6个桥梁桁架结构中的节点静力试验［3］.Gross进行了3个带支撑的框架节点板节点的足尺静力试验，试验结果表明，用Whitmore准则来计算节点板受拉屈服荷载吻合很好［4］.

在上述试验及理论研究的基础上，各国学者利用有限元方法对螺栓连接节点受拉力学性能进行了深入的分析.Richles等利用2维弹性有限元方法，对切口梁块体剪切失效模式进行了研究［5］.Epstein等对T型构件中的块体剪切破坏模式进行了数值分析［6］.Barth等利用有限元方法对宽翼缘T型截面杆件净截面的破坏模式进行了研究［7］.Cem 对节点板受拉时的块体剪切失效模型进行了非线性数值分析，提出了新的节点板块体剪切模式极限承载力公式［8］.目前国外相关规范都提出了节点板受拉破坏模型，并给出了相应的极限承载力计算公式.

我国关于节点板方面的研究较少，沈泽渊等进行了21个焊接节点板静力性能的研究［9］.其研究成果已为我国《钢结构设计规范》（GB 50017—2003）［10］所采用.

图1 钢管塔中的插板节点板连接Fig.1 Gusset plates used in steel tube towers

1 节点板受拉计算理论研究

1.1 传统节点板计算理论

节点板的实际受力情况并不符合材料力学的计算假定，正应力分布不是线性的，而是复杂得多［11］.目前主要有2种近似计算方法来验算节点板的承载力：有效宽度法，块体剪切模型法.

1.1.1 有效宽度法［1］

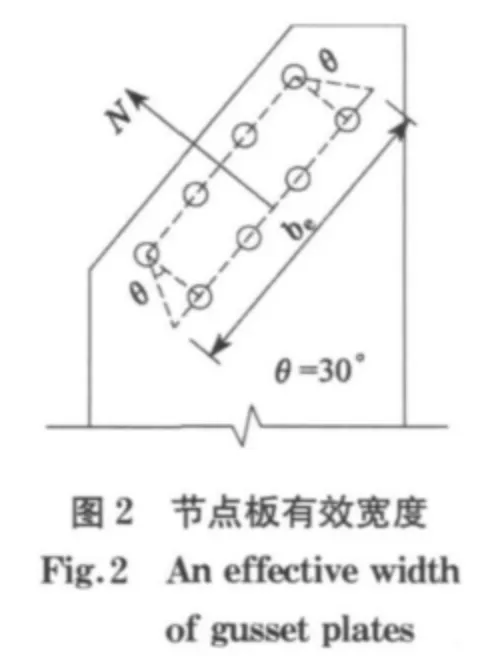
1952年，Whitmore提出了经典的有效宽度法来验算节点是否能够安全承受杆的轴力N，有效宽度be的取法是从第1行螺栓外侧连接件向外以30°角画直线，与通过最后1行螺栓轴线的直线相交所截得的直线宽度（图2）.

节点板破坏时的杆件轴力为

式中：Nu为节点板抗拉极限承载力；t为节点板厚度；fu为节点板钢材抗拉强度.

1.1.2 块体剪切模型法［2］

1985年，Hardash提出块体剪切（图3），并综合考虑连接长度、板厚、螺栓孔径、材料的屈服强度和极限强度、板的形状等影响因素，针对块体剪切性能，提出了节点板在承受拉力作用下的极限承载力公式

式中：Ant为节点板受拉净截面面积；Feff为沿螺栓列外侧作用的有效剪应力；l为连接长度；Cl为连接长度系数；fy为钢材屈服强度；其他符号同前.

1.2 各国节点板计算方法比较

1.2.1 美国规范

在AISC－ASD（89）［12］和AISC－LRFD（2001）［13］中都采用了块体剪切这种组合极限破坏模式.在AISC－ASD 中，认为受拉净截面和受剪净截面同时破坏，而设计承载力考虑了2.0的安全系数，其极限承载力计算公式如下：

式中：Anv为节点板受剪净截面面积；其他符号同前.

美国钢结构规范AISC－LRFD 中，对块体剪切失效模式给出了较为详细的处理，假定受拉面或受剪面达到极限强度时，相应另一个面正好完全屈服，因此，将有2种可能的破坏机理，其中较大的极限荷载起控制作用.第1种破坏模式为假定破坏荷载为当受拉净截面撕裂和受剪毛截面完全屈服；第2 种破坏机理为受剪净截面破坏和受拉毛截面正好完全屈服.其节点板极限承载力计算公式如下：

当fuAnt≥0.6fuAnv时，

当fuAnt＜0.6fuAnv时，

式中：Agv为节点板受剪毛截面面积；Agt为节点板受拉毛截面面积；其他符号同前.

1.2.2 加拿大规范（CSA－S16－01）

加拿大2001年版规范（CSA－S16－01）［14］采用块体剪切来预测节点板的极限承载力，其块体剪切的极限破坏模式假定有2种：一是受拉净截面破坏，受剪毛截面屈服；二是受拉净截面和受剪毛截面同时破坏，其中材料满足Mises准则.节点板承载力取2种破坏模式的较小值.

1.2.3 欧洲规范（Eurocode 3ENV 1993－1－1）

欧洲规范（ENV－1993－1－1）［15］基本假定为受拉

式（10）在欧洲钢结构规范中没有直接给出，但可以从先前关于节点板的失效模式的描述中推导出.

1.2.4 日本规范（Architectral Institute of Japan）［16］

日本规范关于节点板的极限承载力的规定最为保守［17］.该规范采用块体剪切的破坏模式，其受剪面和受拉面均取净截面，块体剪切承载力取下列2种情况的较小值：受剪净截面屈服和受拉净截面破坏；受剪净截面剪切破坏和受拉净截面屈服.其剪切屈服应力、剪切极限应力分别取为对应极限承载力公式如下：

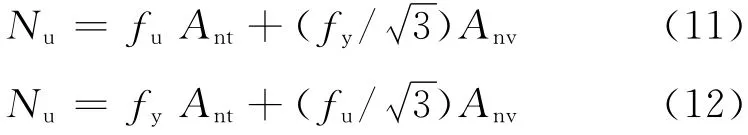
1.2.5 我国钢结构规范

在我国《钢结构设计规范》（GB 50017—2003）［10］中，没有直接给出节点板的极限承载力公式，但可以根据相关公式推导得来.其极限承载力按下式计算：

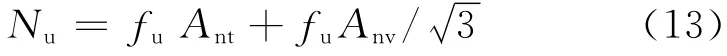
从该式可以看出，我国钢结构规范假定节点板的破坏力学模型为受拉净截面破坏，同时受剪净截面剪切破坏.可见，我国钢结构规范与加拿大钢结构规范中（CSA－S16－01（94））几乎相同.拉剪面同时破坏需要钢材具有足够的延性，这往往与实际不一致.从上述国外计算方法可以看出，各国均采用了块体剪切的联合破坏模式来预测节点板的极限承载力，主要是块体剪切区的破坏模式及相应拉剪面截面积取法略有差别.

1.3 十字节点板计算理论

十字节点板与普通节点的构造对比如图4 所示.对于普通的插板连接，支管轴力通过螺栓将力传到节点板上，节点板通过焊缝将力传到主管上；对于十字插板，支管一部分轴力通过螺栓直接传到主节点板上，另一部分力则通过螺栓传到次节点板上，次节点通过焊缝将力传到主节点板上，主节点板最终将支管全部轴力传到主管上.可见，与普通节点板相比，十字节点板的受力状况要复杂得多，十字节点板在极限状态下主次节点板是否均能出现块体剪切破坏，需要通过相关的试验研究来证明.

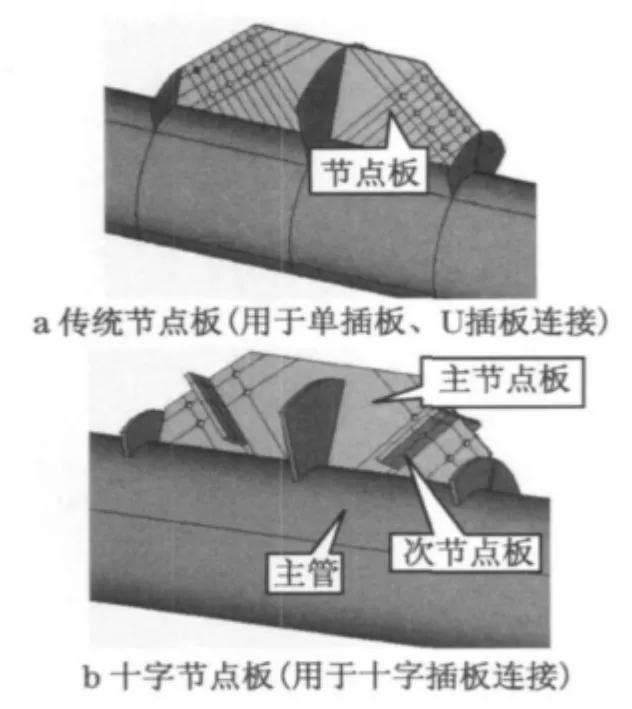
图4 2种节点板构造对比Fig.4 Comparison of two types of gusset plates

2 试验概况

2.1 试件设计

以榕江大跨越塔工程为背景，设计了2 个大尺寸缩尺模型试件（缩尺比例约为1∶3.9），试件编号分别为KC－A，KC－B，2 个试件尺寸相同［18］.试件尺寸及有关参数见表1.

表1 试件尺寸及荷载Tab.1 Details of specimens

2.2 加载原理

试验为单调静力加载.通过大型试验机实现主管轴力加载，两支管轴力则采用液压千斤顶来加载，液压千斤顶与自制反力架连接；试件主管下端通过球面支座支承于自制的反力架底座上，加载中主管底部可以转动.底座通过地脚螺栓与试验室台座固定.试件安装定位及现场试验照片见图5.

图5 试验安装和加载Fig.5 Test set－up

2.3 测试内容

为追踪主管以及各支管的轴向变形，直接或间接测得支管相对于主、支管轴线交点的位移，根据需要在主、支管侧分别布置位移计.节点板受力复杂，在相应位置布置应变花.试件共布置测点85个，具体布置情况详见表2和图6.

表2 测点布置方案Tab.2 Instruction of measurement points

2.4 加载过程及主要现象

2.4.1 加载过程

主管支管按比例加载至设计荷载，之后主管压力恒定，两支管按比例加载至试件破坏.

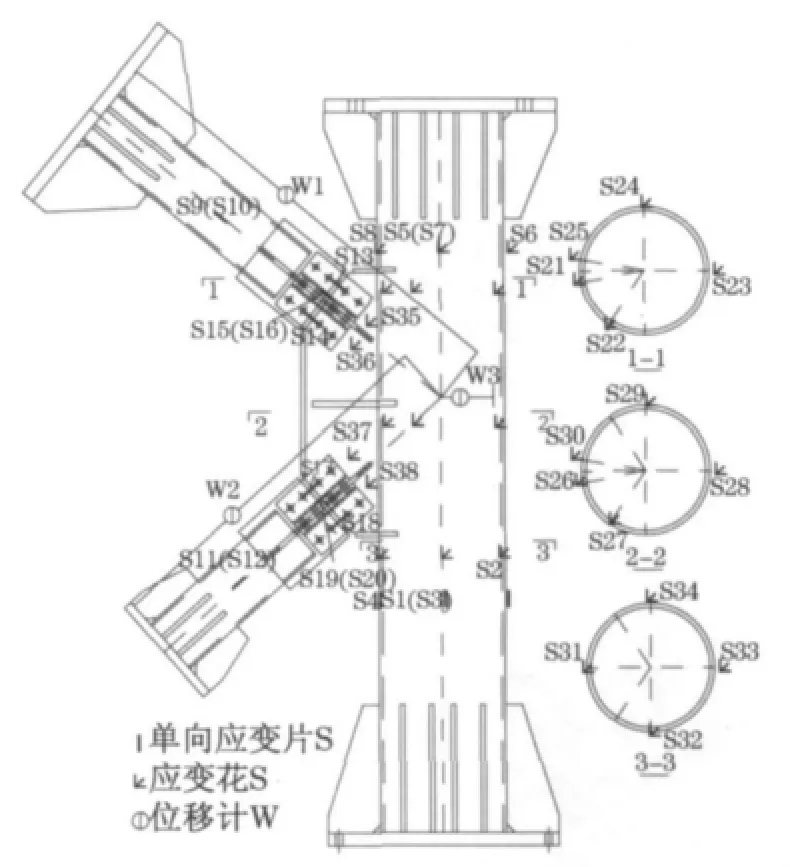
图6 测点布置Fig.6 Layout of measurement points

2.4.2 主要试验现象及破坏模式

两试件的破坏类型相同，均为受拉支管所对应的主节点板及连接螺栓破坏，主节点板破坏部位在块体剪切面上.主管、支管及焊缝没有破坏，也没有明显的变形.两试件支管的极限拉力分别为778kN 和790 kN.典型的破坏照片如图7所示.

图7 试件破坏照片Fig.7 Failure mode of specimen

3 主要结果讨论

3.1 有限元建模说明及模型验证

3.1.1 模型说明

有限元分析软件为ANSYS，考虑到节点板构造复杂，采用3维实体单元SOLID 185建模.其几何模型见图8.材料本构关系按多线性各向同性强化输入（图9a），泊松比为0.3，弹性模量为2.06×105MPa，采用Mises屈服准则.螺栓与螺孔间的传力采用节点耦合来模拟实际的接触传力.模型约束及加载方式如图9b所示.由于本文重点研究节点板螺栓连接处的极限承载力，主管下端约束情况对节点板的极限承载力没有影响，故在有限元分析时，下端部采用固定约束，另一端允许有管轴方向位移；两支管端部仅有管轴方向位移.主管、支管均采用力加载，首先按比例加载至设计荷载，之后主管压力恒定，两支管按比例加载至节点极限承载力.节点板的极限承载力即为最后一个子步所对应的支管轴力.

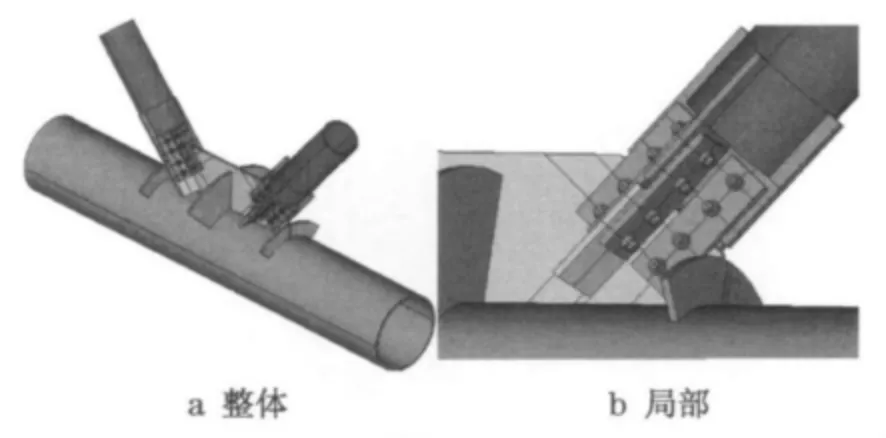
图8 十字节点板几何模型Fig.8 Cross gusset plate geometric model

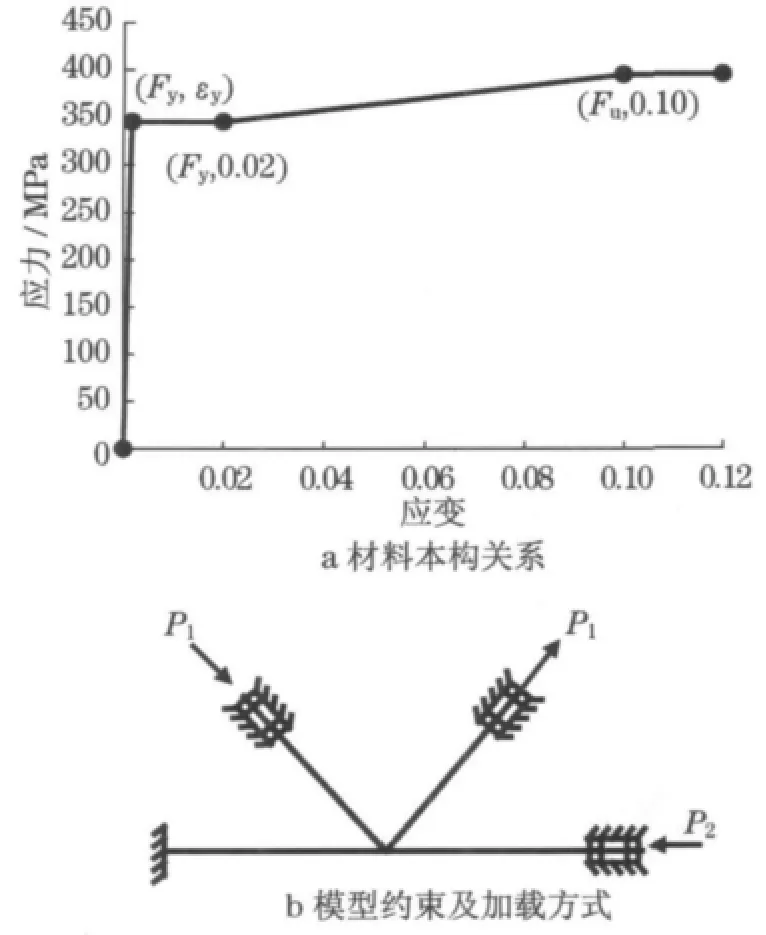
图9 节点板有限元分析模型Fig.9 FE model of gusset plates

3.1.2 模型检验

为考察有限元模型的正确性，以试验模型为原型，设计成相应的传统的U 插板连接，其中节点板厚度及螺栓布置与试验模型完全相同.图10是有限元分析得到的节点板在极限状态下的等效应力云图.可见，极限状态下节点板出现典型的块体剪切破坏，这与目前国外相关规范的假设是一致的.表3列出了节点板极限承载力与国外规范的对比情况.可见，有限元结果与美国规范及欧洲规范符合较好，偏差均为2.6%；与日本规范偏差最大，为15.7%，这是因为日本规范最为保守［17］.为了进一步考察模型的准确性，通过62个U插板模型对影响节点板极限承载力的参数进行了深入分析.图11为相应的有限元结果与欧洲规范的对比情况，其中纵坐标为有限元结果NFEM与欧洲规范计算值Nu（式（10））的比值NFEM／Nu，横坐标为模型参数与原始模型相应参数的比值β.可见，有限元结果与欧洲规范的一致性很好，其比值主要在1.0～1.1之间.这充分说明本文有限元模型计算结果是准确可信的.

表3 节点板极限承载力与国外规范对比Tab.3 Comparisons of ultimate capacity of U gusset plate

图11 U 插板节点板有限元分析结果与欧洲规范比较Fig.11 Comparisons of ultimate capacity of U gusset plate between FEM and Eurocode 3

3.2 试验结果与有限元分析结果讨论

3.2.1 结果讨论

图12a为试验及有限元分析得到的受拉支管端部的荷载—位移曲线.可以看出，当荷载小于650kN（设计荷载为400kN），节点板整体表现为弹性，变形很小；当荷载大于650kN，节点板塑性区域逐步扩大，相应变形增大，其极限荷载分别为778，771kN，二者吻合很好.从图中还可以看出，在极限荷载之前，节点板经历了较大的塑性变形，这与普通的节点板是相似的.试验测得的变形要比有限元结果大，且曲线多处有弯折，这主要是因为节点插板连接的螺栓与螺孔间有间隙，加载过程中螺栓出现滑移，试验中也听到了滑移的声音，普通抗剪螺栓（非高强螺栓摩擦型连接）在弹性阶段会发生滑动，文献［2］的试验也证实这一点.由于本文重点研究节点板的极限承载力，试验中弹性阶段螺栓的滑移对节点极限承载力没有影响，故有限元分析中忽略了螺栓的滑移.

图12b为试验及有限元分析得到的节点板关键点荷载—应变曲线.可以看出，该区域节点板较早就进入塑性，从整个试验来看，该区域没有破坏，也没有出现明显的变形；从最终的破坏模式来看，试验结果为主节点板第1排螺栓破坏及其节点板螺孔端部被剪坏，试验结束时，主节点板第2排螺孔已出现较大的塑性变形，可见主节点板的拉剪面已进入塑性.而次节点板第1排螺孔塑性变形很小，第2排螺孔没有明显的变形（图7）.图13为有限元分析得到的十字节点板在极限状态下的等效应力云图，可见，主节点板块体拉剪面及节点板根部区域进入塑性，主节点板出现典型的拉剪联合破坏（即块体剪切破坏）；次节点板大部分拉剪区则处在弹性阶段.可见，有限元分析结果与试验结果较为吻合.

3.2.2 十字节点板与普通节点板的极限承载力比较

试验得到的十字节点板极限承载力分别为790，778kN，有限元结果为771kN.从上文的分析可知，采用相同螺栓布置的传统U 插板的极限承载力为647kN，可见十字节点板的极限承载力比普通节点板高出约20%，表明十字节点板具有较好的受力性能.

3.2.3 十字节点板极限承载力与理论值比较

目前国内外相关规范都没有对十字节点板的极限承载力作出规定，为了进一步分析节点板的极限承载力，结合各国规范传统节点板的计算理论，针对十字节点板提出3个理论值.

（1）理论计算值1（Nu，1）

理论值1为主节点板受拉净截面及受剪毛截面同时破坏所对应的承载力，其中材料属性满足von Mises准则，理论值1的计算公式如下：

式中：At1为主节点板受拉净截面面积，At1＝（m－1）（e3－d）t；e3为螺栓垂直受力方向的间距；m为螺栓的列数；Av1为主节点板受剪毛截面面积，Av1＝2（n－1）（e1＋e2）t；e1为顺受力方向的螺栓间距；e2为螺栓端距；n为螺栓的排数.

（2）理论计算值2（Nu，2）

理论值2为主节点板及次节点板受拉净截面破坏，主节点板及次节点板受剪毛截面屈服所对应的十字节点板的承载力，材料属性满足von Mises准则，即τy＝0.57fy，理论值2的计算公式如下：

式中：At为主节点板及次节点板受拉净截面面积之和，在本文中At＝2At1－t2；Av为主、次节点板受剪毛截面面积，Av＝2Av1.

（3）理论计算值3（Nu，3）

理论值3为主节点板及次节点板受拉净截面屈服，主节点板及次节点板受剪毛截面破坏所对应的承载力，材料属性满足von Mises 准则，即τu＝0.57fu，理论值3的计算公式如下：

表4列出了各理论值与有限元及试验结果的对比情况.可以看出，试验及有限元结果是理论值1的1.25倍，与理论值2和3相比，大致为0.7倍.这表明十字节点板的极限承载力比主节点板拉剪面同时破坏所对应的承载力大，比整个十字节点板剪切破坏所对应的承载力要小.这是因为节点板的极限状态为十字节点板中主节点板的拉剪面能进入塑性，而次节点板面的应力还处于弹性状态.

表4 十字节点板极限承载力比较Tab.4 Comparisons of ultimate capacity of cross gusset plate

4 极限承载力有限元参数研究

以试验模型为基础，进一步研究了节点板厚度t、螺栓间距（e1，e3）及端距（e2）（图14），强屈比（fu／fy）对节点板极限承载力的影响，分析结果见图15.图中纵坐标为有限元结果与各理论值的比值，横坐标为模型参数与原始模型相应参数的比值β.可以看出，有限元结果与理论值1的比值主要在1.2～1.3之间，与1.25基本呈对称分布；有限元结果与理论值2和3的比值主要在0.64～0.72之间.这充分表明，当节点板参数变化时，有限元结果与各理论值的比值总体变化较小.

图14 十字节点板构造Fig.14 Details of cross gusset plate

图15 十字节点板极限承载力有限元参数分析结果Fig.15 Ultimate capacity of cross gusset plate between FEM parameters results and theory results

5 十字节点板极限承载力及设计公式

根据试验及有限元参数研究结果，考虑便于实际工程应用，设计时建议采用与理论值1的关系来代表十字节点板的极限承载力，即

按照极限状态设计理论，节点板的设计公式为

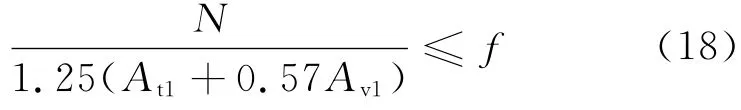
式中f为钢材强度设计值.

6 结论

（1）为检验十字节点板有限元模型的有效性，对62个U 插板连接节点板模型进行了有限元非线性分析，其结果与国外相关规范符合较好，表明本文节点板有限元模型是正确的.同时，十字节点板的试验结果与有限元分析结果一致性较好，也证明本文十字节点板有限元模型是正确的.

（2）试验和有限元分析结果表明，十字节点板的极限承载力比传统的U 插板高20%，表明十字节点板具有优良的受力性能，安全可靠，可用于实际工程.

（3）对于十字节点板的破坏模式，试验结果为主节点板拉剪区进入塑性，节点板破坏出现块体剪切区域内；次节点板大部分拉剪区没有明显塑性变形；有限元结果为主节点板拉剪区及节点板根部区域进入塑性，出现典型的块体剪切破坏，而次节点板拉剪主要区域处于弹性状态；可见，有限元分析结果与试验结果是吻合的.

（4）十字节点板的极限承载力大于主节点板块体剪切破坏承载力，但小于十字节点板整体块体剪切承载力.原因是极限状态时，主节点板块体剪切区大部分能进入塑性，而次节点板块体剪切区大部分处于弹性状态.

（5）试验及有限元参数分析结果表明，十字节点板的极限承载力与主节点板块体剪切破坏承载力、十字节点板整体块体剪切承载力大小关系较为恒定，大致是前者的1.25倍，是后者的0.7倍.

（6）根据试验研究和有限元分析结果，从极限状态出发，提出了十字节点板的极限承载力计算公式和设计公式.

［1］ Whitmore R E.Experimental investigation of stresses in gusset－plates ［R］.Knoxville：University of Tennessee.Engineering Experiment Station，1952.

［2］ Hardash S G，Bjorhovde R.New design criteria for gusset plates in tension［J］.AISC Engineering Journal，1985，22（2）：77.

［3］ Yamamoto K，Akiyama N，Okumura T.Buckling strength of gusseted truss joints［J］.Journal of Structural Engineering：ASCE，1988，114（3）：575.

［4］ Gross J L.Experimental study of gusseted connections［J］.Engineering Journal：Am Inst of Steel Constr，1990，27（3）：89.

［5］ Ricles J M，Yura J A.Strength of double－row bolted－web connections［J］.ASCE Journal of Structural Engineering，1983，109（1）：126.

［6］ Epstein H I，Ginnis M J.Finite element modeling of block shear in structural tees［J］.Computers and Structures，2000，77（5）：571.

［7］ Barth K E，Orbison J G，Nukala R.Behavior of steel tension members subjected to uniaxial loading ［J］.Journal of Constructional Steel Research，2002，58：1103.

［8］ Cem Topkaya.A finite element parametric study on block shear failure of steel tension members［J］.Journal of Constructional Steel Research，2004，60（11）：1615.

［9］ 沈泽渊，赵熙元.焊接钢桁架外加式节点板静力性能的研究［J］.工业建筑，1987（8）：19.SHEN Zeyuan，ZHANG Xiyuan.A study on static behavior of gusset plate of welding steel truss［J］.Industrial Construction，1987，（8）：19.

［10］ 中华人民共和国建设部.GB 50017—2003 钢结构设计规范［S］.北京：中国计划出版社，2003.Ministry of Construction of the P R China.GB 50017—2003 Code for design of steel structures［S］.Beijing：China Planning Press，2003.

［11］ 陈绍蕃.钢结构设计原理［M］.2版.北京：科学出版社，2003.CHEN Shaofan.Design principle of steel structures［M］.2nd ed.Beijing：Science Press，2003.

［12］ American Institute of Steel Construction.AISC－ASD89 Allowable stress design specification for structural steel buildings［S］.9th ed.Chicago：American Institute of Steel Construction，1989.

［13］ American Institute of Steel Construction.AISC－LRFD2001 Load and resistance factor design specification for structural steel buildings［S］.3rd ed. Chicago： American Institute of Steel Construction，2001.

［14］ Canadian Standian Association.CAN／CSA－S16－01 Limit states design of steel structures［S］.Toronoto：Canadian Standian Association，2001.

［15］ European Committee for Standardization.Eurocode 3：ENV 1993－1－1 Design of steel structures［S］.Brussels：European Committee for Standardization，1992.

［16］ Architectural Institute of Japan.Standard for limit state design of steel structures［S］.Tokyo：Architectural Institute of Japan，1990.

［17］ Kulak G L，Wu E Y.Shear lag in bolted angle tension members［J］.ASCE Journal of Structural Engineering，1997，123（9）：1144.

［18］ 邓洪洲.榕江大跨越节点抗震试验报告［R］.上海：同济大学建筑工程系，2009.DENG Hongzhou.Seismic experimental report on the joint used in Rongjiang steel tube tower［R］.Shanghai：Tongji University.Department of Building Engineering，2009.