高强钢筋混凝土梁裂缝宽度的试验研究和分析

周建民，王 眺，陈 飞，赵 勇

（同济大学 建筑工程系，上海200092）

混凝土结构中使用高强钢筋，可明显减少钢筋用量，显著改善目前框架结构梁、柱节点和框架柱钢筋拥挤的现象［1］.但在实践中，配置高强度钢筋的混凝土构件按《混凝土结构设计规范》（GB 50010—2002）［2］（以下简称《规范》）验算裂缝宽度时，裂缝宽度大都超过限值，限制了高强钢筋的使用.有研究指出，按规范裂缝宽度公式计算值要比实测值大，它是否适用于高强度钢筋本身值得研究［3－5］.本文通过14根配置500 MPa钢筋梁的受弯性能试验，并结合相关试验数据，分析了现行裂缝宽度计算公式不适用于高强钢筋的原因，提出了规范公式的修改建议.

1 试验

1.1 试验概况

试验设计了10根矩形梁（JL1—JL10）和4根T形梁（TL11—TL14），全部配置500MPa高强度钢筋.表1和图1中，b，h，L分别为试验梁宽度、高度和跨度，b′f和h′f分别为试验梁翼缘宽度和厚度，c为试验梁保护层厚度.试件在纯弯段不配置箍筋，为了便于量测梁底面裂缝，采用四分点反向加载方案，加载装置和量测内容见图2.图中.G－x表示钢筋的应变测点，f－x表示试验挠度测点.为观测裂缝宽度，试验前将梁侧及受拉底面用白色涂料刷白，并绘制50 mm×50 mm 的网格；试验时借助放大镜用肉眼查找裂缝；构件开裂后立即对裂缝的发展情况进行详细观测，用读书放大镜及裂缝观测仪等工具测量各级荷载下的裂缝宽度，当量测钢筋应变超过2 000×10－6后停止观测裂缝.测点位置见图3.

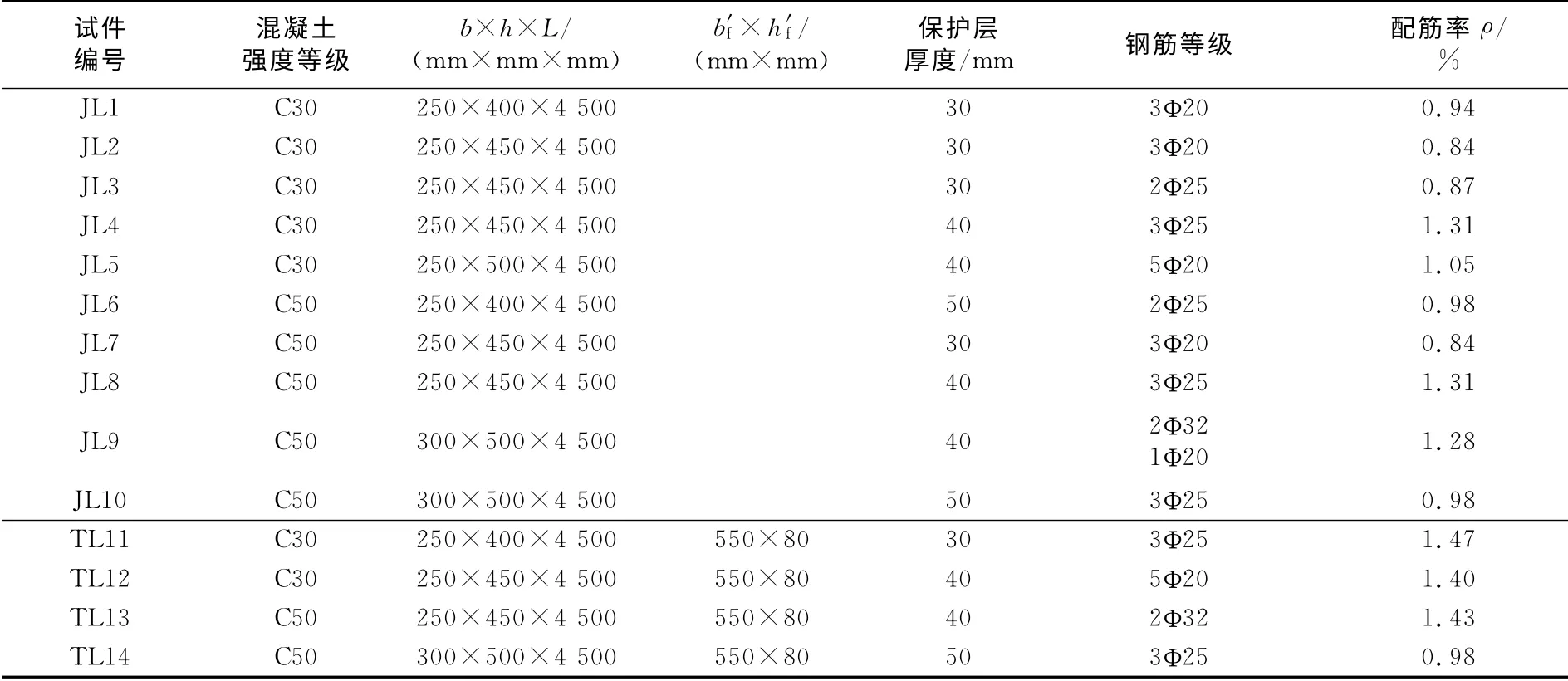
表1 试件设计参数Tab.1 Details of specimens design properties

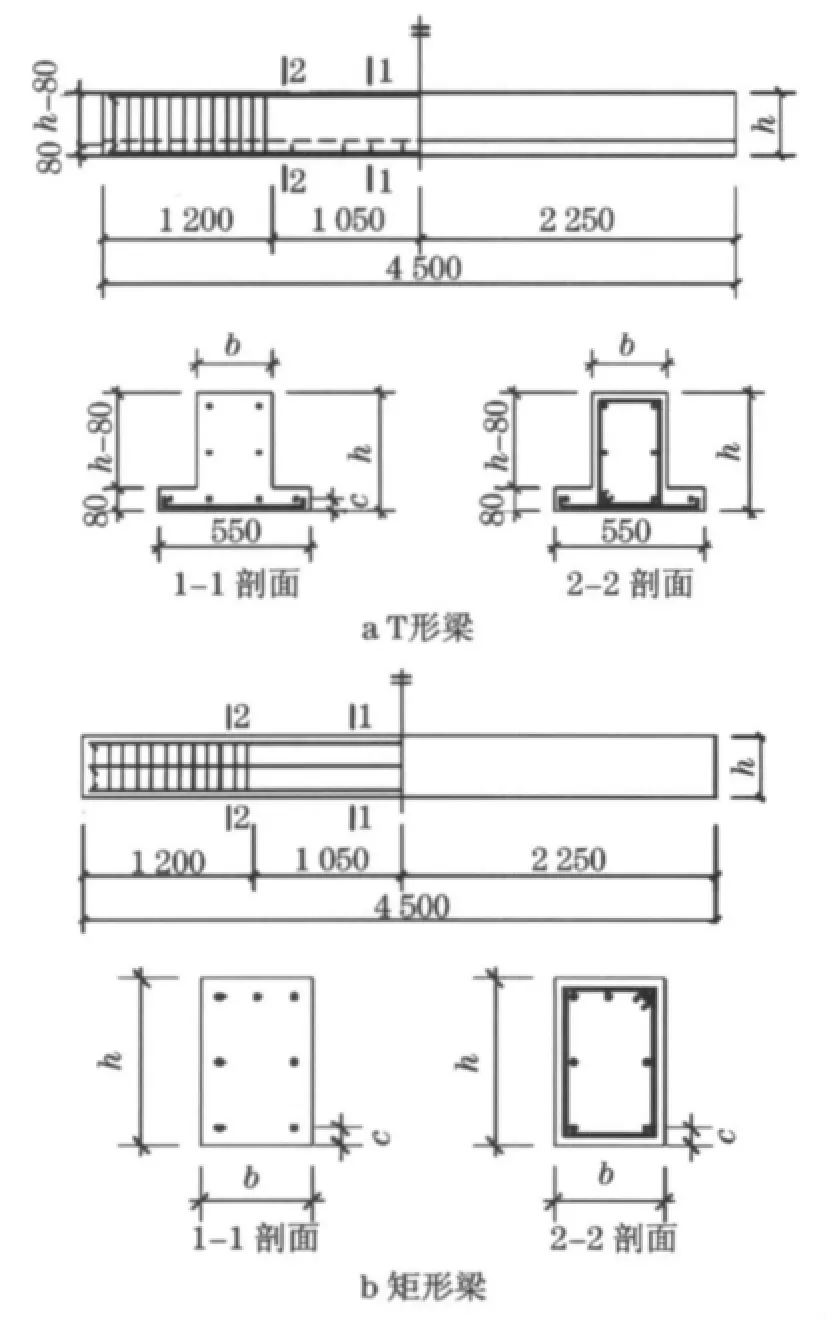
图1 试件详图（单位：mm）Fig.1 Details of specimens（unit：mm）

1.2 试件裂缝开展情况

当荷载加至0.2Pu～0.3Pu时，在跨中截面发现1条或多条垂直裂缝，其中Pu为实测破坏荷载.裂缝首先出现在构件边缘处，一般侧面裂缝与底面裂缝可以贯通，侧面上裂缝高度一般可达到梁高的1／4左右，此时裂缝宽度较小.随着荷载的增加，裂缝条数逐渐增多，原先出现的侧面裂缝向梁受压边缘延伸，梁底面裂缝向底面轴心延伸，并迅速贯穿整个梁底面，裂缝宽度进一步增大.当荷载进一步增大至0.4Pu～0.5Pu时，构件不再产生新的主裂缝，裂缝间距处于稳定，裂缝宽度随着荷载增加而增大，局部会产生裂缝宽度较小的次生裂缝.接近极限荷载时，1条主裂缝宽度迅速增大直至混凝土被压碎.试验表明，配置500 MPa钢筋的混凝土梁裂缝开展过程和变形曲线与普通钢筋混凝土梁的情况基本接近.图4 为JL1梁的弯矩挠度关系和裂缝开展情况.图中，M为试验梁截面弯矩，Mu为试验梁极限抗弯承载能力.

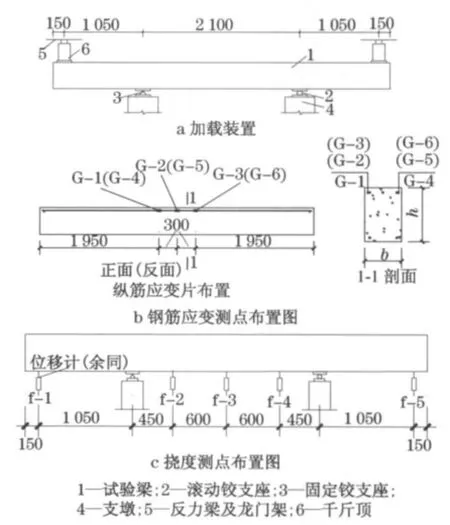
图2 加载装置和量测内容（单位：mm）Fig.2 Test device（unit：mm）

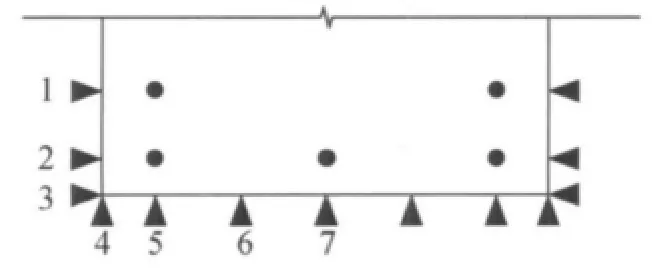
图3 裂缝测点位置图Fig.3 Measuring points location

图4 JL1挠度曲线和裂缝开展试验结果Fig.4 Deflection and cracks distribution of JL1

2 试验结果分析

2.1 试验梁裂缝开展图比较

JL2与JL3截面尺寸相同，底面保护层厚度均为30mm，JL2配置3根直径20mm 的钢筋，而JL3则配置2 根直径25 mm 的钢筋，配筋率分别为0.84%和0.87%.由图5的裂缝开展图对比可知，JL2的裂缝明显多于JL3.因此可以认为配筋率和钢筋直径是一对重要的影响参数.

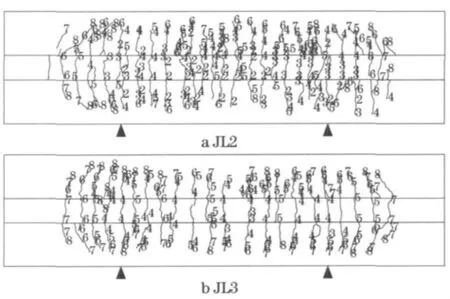
图5 梁裂缝分布情况Fig.5 Beams cracks distribution

2.2 裂缝宽度沿截面竖向及横向的分布规律

为了研究裂缝宽度沿裂缝高度的分布规律，本次试验追踪一些典型的裂缝.这些裂缝既有沿截面高度发展的侧面裂缝，也有沿截面宽度发展的底面裂缝.

2.2.1 侧面裂缝宽度沿梁高的变化规律

为了和普通钢筋混凝土梁对比，图6 分别给出了高强钢筋混凝土梁和普通钢筋混凝土梁裂缝宽度沿梁高变化规律［7］.从试验结果来看，高强钢筋混凝土梁梁侧面沿梁高的变化规律基本和普通钢筋混凝土梁相同，距梁受拉底面边缘越远，裂缝宽度越小；裂缝在底面边缘处的宽度最大.

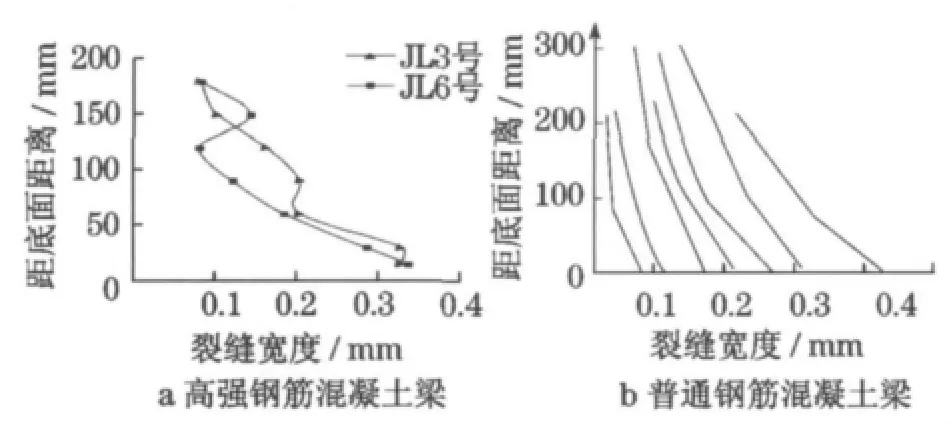
图6 裂缝宽度沿梁高变化规律Fig.6 Cracks－width variation along height

2.2.2 受拉底面裂缝宽度沿梁宽的变化规律

本次试验，采用了反向加载，得到了梁底裂缝变化规律.从试验结果来看，梁底面裂缝宽度沿梁宽变化规律是靠近边缘处的裂缝宽度较大；但个别裂缝宽度存在跳跃的现象，可能是由于材料不均匀性等因素造成.图7是JL5裂缝宽度沿梁宽度变化规律.

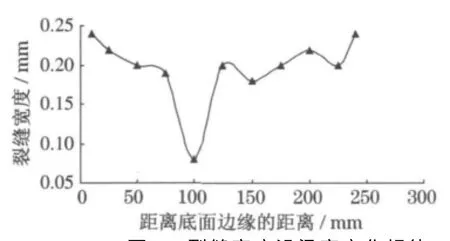
图7 裂缝宽度沿梁宽变化规律Fig 7 Cracks－width variation along width of beam

2.2.3 不同位置处的裂缝宽度试验值分析

本次试验中不仅量测了梁纯弯段侧面受拉纵筋位置处的裂缝宽度，还量测了如图3所示的其他几个关键位置处的裂缝宽度.

由试验结果（图8）可以发现：各位置处的裂缝宽度基本与弯矩呈线性关系，裂缝宽度随着弯矩的增大而增大；梁侧面纵向受拉钢筋位置处的裂缝宽度小于其他位置处的裂缝宽度，当配置双层钢筋时上层钢筋位置处的裂缝宽度略小于底层钢筋位置处的裂缝宽度；除个别梁外，侧面边缘处的裂缝宽度与底面边缘处裂缝宽度大致相当，但都较其他位置处的裂缝宽度大.

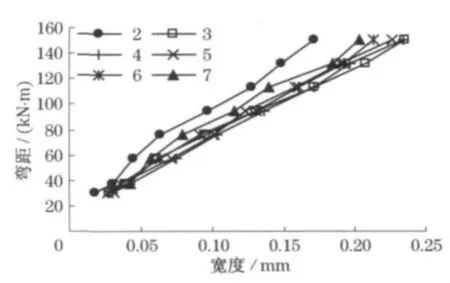
图8 平均裂缝宽度与弯矩关系Fig.8 Relationship between average crack－width and moment

2.2.4 裂缝宽度统计分析

根据本次试验获得的侧面纵筋位置处的裂缝宽度数据进行统计分析，考察其分布规律，从而得到短期裂缝宽度扩大因数τs.分别将试验梁各级荷载下的裂缝宽度与相应荷载下的平均裂缝宽度之比作为统计值.对样本作K－S检验（柯尔莫哥洛夫－斯密尔洛夫检验），显著性水平0.05，除了JL9和TL13外，侧面纵向钢筋位置处的裂缝宽度与平均裂缝宽度的比值大致呈正态分布，裂缝宽度变异因数平均为0.383，仍取为0.400，因此裂缝宽度扩大因数τs可取为：τs＝1＋1.654×0.4≈1.66.

3 与《混凝土结构设计规范》（GB50010—2002）公式计算值的对比及分析

3.1 与规范公式计算值的对比

将本次平均裂缝间距、平均裂缝宽度和最大裂缝宽度试验结果与按《规范》裂缝宽度计算公式的计算值进行比较，结果见图9.其中，lcr为平均裂缝间距计算值，lcr，t为平均裂缝 间距试验值，wm与wm，t分别为平均裂缝宽度计算值与试验值，wmax与wmax，t分别为最大裂缝宽度计算值与试验值.由图9可见，规范计算的平均裂缝间距比试验值略大，不到10%；而规范平均裂缝宽度计算值比试验值大55%；最大裂缝宽度计算值比试验值大59%.可见规范公式用来计算配500 MPa级钢筋的混凝土梁受弯裂缝宽度时偏大较多.

图9 试验结果与规范计算值比较Fig.9 Comparison of the test results and the calculated value

3.2 规范公式偏差原因的分析

《规范》裂缝宽度计算模式的经验因数来源于过往试验梁的数据资料，这些梁的钢筋工作应力较低、钢筋直径和保护层厚度较小，导致了基于过往试验资料的规范公式用来计算近期试验梁的裂缝宽度时偏大.下面通过过往试验［6－7］与近期试验［3－5，8－15］的试验数据，研究和分析规范裂缝宽度计算公式在计算高强度钢筋混凝土梁裂缝宽度时产生较大偏差的主要原因.

3.2.1 裂缝平均间距

《规范》按综合理论建立平均裂缝间距公式，考虑保护层厚度对裂缝宽度的影响和钢筋可能出现的滑移，即现行规范公式中的裂缝间距lcr，1＝1.9c＋0.08deq／ρte.式中，deq为受拉区纵向钢筋的等效直径；ρte为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率.但上述公式是建立在保护层较小的混凝土梁的试验结果上，是否适用于配置保护层厚度较厚的高强钢筋混凝土梁值得研究.根据全部样本中满足c≥25 mm，直径d≥16 mm，ρ≥0.5%条件的114个平均裂缝间距数据回归，采用K1c＋K2deq／ρte模型回归分析因数K1＝1.928，K2＝0.069；而根据配置400 MPa，500 MPa钢筋的样本中满足c≥25 mm，d≥16 mm，ρ≥0.5%条件的83个平均裂缝间距数据回归，则K1＝1.611，K2＝0.078，即建议公式的裂缝间距为

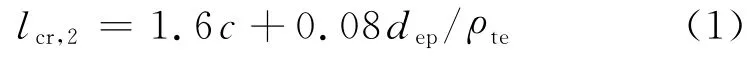
当保护层厚度变化时，式（1）和规范公式计算的平均裂缝间距计算结果见表2.表中，lcr，1是规范公式的计算 值，lcr，2是 建 议 公 式 计 算 值，lcr，t为 试 验 值.从总体上看，平均裂缝间距按建议公式和规范公式的计算结果相差在7%左右，从保持规范公式的延续性出发可以不进行修正.表2 裂缝间距计算值与实测值比较

Tab.2 Comparison of the calculated average cracks spacing and the test results

c＜30mm c≥30mm 总体指标lcr，1 lcr，t lcr，2 lcr，t lcr，1 lcr，t lcr，2 lcr，t lcr，1 lcr，t lcr，2 lcr，t 1.077 1.014 1.111 1.028 1.086 1.016变异系数 0.142 0.144 0.104 0.100 0.135 0.134样本数均值65 65 21 21 83 83

3.2.2 综合影响系数

我国规范裂缝宽度wm公式采用半经验半理论模式［16］：

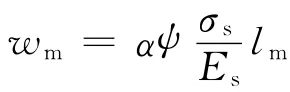
式中：wm为规范公式平均裂缝宽度计算值；α为构件受力特征因数；ψ为裂缝间纵向受拉钢筋应变不均匀因数；σs为按荷载效应的标准组合计算的钢筋混凝构件纵向受拉应力；Es为钢筋弹性模量；lm为混凝土裂缝间距.α反映了混凝土对裂缝宽度的影响，其值是通过试验数据回归得到的，规范分析了109根梁试验数据后，得到α＝0.85.但要指出，α＝0.85是基于低钢筋应力时的数据回归得到的，是否适用于高钢筋应力的情况有待研究.

混凝土开裂后，在2条主裂缝间的混凝土会出现次裂缝，如图10所示.次裂缝一方面减弱了混凝土与钢筋的黏结应力，增大了钢筋应变不均匀因数；另一方面，次裂缝也会增大主裂缝间混凝土的变形，减小了主裂缝的宽度，可看成次裂缝“分担”了一部分主裂缝宽度，使主裂缝宽度减小.显然，随着钢筋应力的增大，次裂缝会增多.因此，讨论高应力情况下的次裂缝展开情况显得十分必要.

图10 混凝土主次裂缝开展情况Fig.10 Developments of cracks and sub cracks in concrete beams

虽然次裂缝很难用肉眼直接观测到，但钢筋应变不均匀因数可以间接反映次裂缝的开展情况，钢筋应变不均匀因数变大，次裂缝发展得越多.本次14根梁钢筋应变不均匀因数的试验值和计算值比值ψt／ψ＝1.14，变异因数为0.152.另外，东南大学课题组的研究报告［8］也得到了相似的结果，其ψt／ψ＝1.07，变异因数为0.155.可见现行规范低估了高钢筋应力情况下次裂缝的开展，忽略了其抑制主裂缝宽度的有利影响.

在钢筋应力较高时，分别引入修正因数c1，c2.将ψ修正为c1ψ，α修正为c2α，即

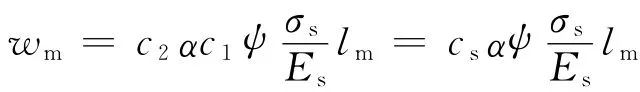
式中：ψ值计算仍采用规范公式；cs为考虑混凝土和钢筋应变不均匀因数对平均裂缝宽度影响的综合因数，由试验数据确定.

4 平均裂缝宽度公式的建议

由前述知，当钢筋工作应力较大时，按规范的裂缝计算公式计算值偏差显著，主要原因在于公式中没有考虑钢筋工作应力对裂缝间距、次裂缝的影响.其解决途径有2条：在现有规范公式基础上增加一个钢筋高工作应力（σs＞200 MPa）的裂缝宽度综合调整因数cs，以考虑高应力的影响，或者直接采用能考虑上述因素的裂缝宽度计算模式.

按第一种思路，有

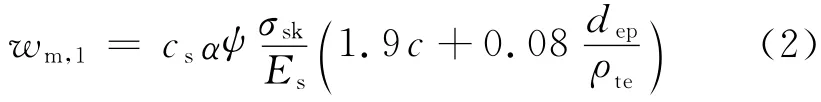
由收集到的73根高强钢筋混凝土梁裂缝宽度的数据（σs＞200 MPa）［3－15］统计分析得到cs取为0.77，变异因数为0.300.

作者在20年前根据裂缝综合理论提出的能考虑众多影响因素的受弯构件平均裂缝宽度计算公式为

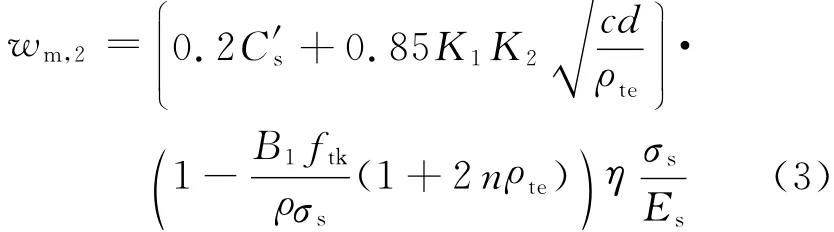
公式符号意义和具体取值见文献［17］.

对301个平均裂缝宽度试验值与式（2），（3）计算值进行比较，如图11所示.其中wm，1／wm，t均值为1.004，变异因数为0.300，wm，2／wm，t均值为1.030，变异因数为0.310.从图11可见，建议公式与试验值符合良好.

图11 平均裂缝宽度计算值与试验值比较Fig.11 Comparison of calculated average cracks width and test results

5 结论

（1）配置500 MPa钢筋的混凝土梁裂缝展开过程与配普通钢筋的混凝土梁基本相同.

（2）配筋率和钢筋直径是一对影响参数，当配筋面积相同时，钢筋直径越小，裂缝宽度越小.

（3）裂缝形态追踪发现：梁侧面裂缝宽度沿梁高度变化趋势是离梁受拉底面边缘越远，裂缝宽度越小；裂缝在底面边缘处的宽度最大，梁底面裂缝宽度靠近边缘处的裂缝宽度较大.

（4）通过不同位置裂缝宽度的量测发现：各位置处的裂缝宽度基本与弯矩呈线性关系，裂缝宽度随着弯矩的增大而增大；梁侧面纵向受拉钢筋位置处的裂缝宽度小于其他位置处的裂缝宽度.

（5）在钢筋高应力情况下，《混凝土结构设计规范》（GB 50010—2002）的裂缝间距和平均裂缝宽度公式的计算值与实测值相比明显偏大.

（6）对试验结果和相关数据分析后，建议按式（2）或式（3）计算裂缝宽度.

［1］ 刘立新，谢丽丽，于秋波.500 MPa级钢筋混凝土构件受力性能与工程应用［J］.建筑结构，2006，36（增）：66.LIU Lixin，XIE Lili，YU Qiubo.Study on the behavior of reinforced concrete members with 500 Mpa steel bars under loading and its applications in civil engineering［J］.Buiding Structure，2006，36（Suppl.）：66.

［2］ 中华人民共和国建设部.GB 50010—2002 混凝土结构设计规范［S］.北京：中国建筑工业出版社，2002.Ministry of Construction of P R China.GB 50010—2002Code for design of concrete structures ［S］.Beijing： China Architecture ＆Building Press，2002.

［3］ 李志华.配置高强钢筋混凝土梁受弯性能研究［D］.上海：同济大学土木工程学院，2008.LI Zhihua.Research on flexural performance of concrete beam reinforced with high－strength rebars ［D］.Shanghai：Tongji University.College of Civil Engineering，2008.

［4］ 尚世仲.配高强钢筋混凝土梁的受弯性能试验研究［D］.上海：同济大学土木工程学院，2007.SHANG Shizhong. Experimental research on flexural performance of concrete beam reinforced with highstrength rebars［D］.Shanghai：Tongji University.College of Civil Engineering，2007.

［5］ 同济大学土木工程学院.配500 MPa细晶粒钢筋的混凝土梁受弯性能试验研究报告［R］.上海：同济大学土木工程学院，2006.Report on HRB500MPa concrete beams bending behavior test［R］.Shanghai： Tongji Unviversity.College of Civil Engineering，2006.

［6］ 白生翔，黄成若.钢筋混凝土构件试验数据［R］.北京：中国建筑科学研究院，1985.BAI Shenxiang，Huang Chengruo.Test data on concrete beams test ［R］.Beijing：China Academy of Building Research，1985.

［7］ 东南大学.钢筋混凝土受弯构件变形和裂缝的计算［M］.北京：中国建筑工业出版社，1977.Study on the methods for computing deflections and crack width of reinforced concrete flexural members［M］.Beijing：China Archtiecture ＆Building Press，1977.

［8］ 东南大学课题组.国内外相关规范关于钢筋混凝土构件裂缝宽度计算方法比较［R］.南京：东南大学土木工程学院，2008.Comparison of concrete structures crack width formulation in domestic and foreign criterions［R］.Nanjing：Souteheast University.College of Civil Engineering，2008.

［9］ 李美云.HRB400级钢筋混凝土构件受力性能的试验研究［D］.郑州：郑州大学土木工程学院，2003.LI Meiyun.The study of the mechanical property of HRB400 reinforced concrete members［D］.Zhengzhou：Zhengzhou University.College of Civil Engineering，2003.

［10］ 梁书亭，蒋永生，姜宁辉.高强钢筋高强混凝土梁裂缝宽度验算方法的研究［J］.南京建筑工程学院学报，1998，45（2）：10.LIANG Shuting，JIANG Yongsheng，JIANG Ninghui.Research for calculation method of cracking width of high strength concrete beams［J］.Journal of Nanjing Architectural and Civil Engineering Institute，1998，45（2）：10.

［11］ 王命平，张自琼，耿树江.500 MPa级带肋碳素钢筋混凝土简支梁的受弯试验［J］.工业建筑，2007，37（8）：39.WANG Mingping，ZHANG Ziqiong，GENG Shujiang.Experiment of reinforced concrete simply supported beam with 500 MPa ribbed carbon bars under bending ［J］.Industrial Construction，2007，37（8）：39.

［12］ 王铁成，李艳艳，戎贤.配置500 MPa钢筋的混凝土梁受弯性能试验［J］.天津大学学报，2007，40（5）：507.WANG Tiecheng，LI Yanyan，RONG Xian.Test for bending behavior of reinforced concrete beam with 500 MPa steel bar［J］.Journal of Tianjin University，2007，40（5）：507.

［13］ 肖红菊.HRB400级钢筋混凝土梁抗弯性能研究［D］.郑州：郑州大学土木工程学院，2006.XIAO Hongju.Experimental research on the bend behavior of HRB400 reinforced concrete beams ［D］.Zhengzhou：Zhengzhou University.College of Civil Engineering，2006.

［14］ 徐风波.HRB500级钢筋混凝土梁正截面受力性能试验及理论研究［D］.长沙：湖南大学土木工程学院，2007.XU Fengbo.Experimental and theoretical research on flexural behavior of reinforced concrete beams with HRB500 bars［D］.Changsha：Hunan University.College of Civil Engineering，2007.

［15］ 张艇.HRB500级钢筋混凝土构件受力性能的试验研究［D］.郑州：郑州大学土木工程学院，2004.ZHANG Ting.Experimental research on forced performance of concrete beam reinforced with grade HRB500 reinforcement ［D］.Zhengzhou：Zhengzhou University.College of Civil Engineering，2004.

［16］ 蓝宗建，丁大钧.钢筋混凝土受弯构件裂缝宽度的计算［J］.南京工学院学报，1985（2）：64.LAN Zongjian，DING Dajun.Calculation for crack width fo reinforced concrete members with flexure［J］.Journal of Nanjing Institute of Technology，1985（2）：64.

［17］ 周建民，胡匡璋.加筋混凝土构件裂缝宽度计算方法的研究［J］.上海铁道大学学报：自然科学版，1990，11（3）：1.ZHOU Jianmin，HU Kuangzhang.Studies on calculating method for the crack width in reinforced concrete members［J］.Journal of Shanghai Institute of Railway Technology，1990，11（3）：1.