结合广义Armijo步长搜索的一类记忆梯度算法

朱 帅，王希云

(1.山西大同大学 工学院 山西 大同 037003； 2.太原科技大学 应用科学学院 山西 太原 030024)

结合广义Armijo步长搜索的一类记忆梯度算法

朱 帅1，王希云2

(1.山西大同大学 工学院 山西 大同 037003； 2.太原科技大学 应用科学学院 山西 太原 030024)

给定记忆梯度算法搜索方向中的参数一个假设条件，从而确定它的一个取值范围, 使其在此范围内取值均能得到目标函数的充分下降方向，由此提出一类新的记忆梯度算法.在去掉迭代点列有界和广义Armijo步长搜索下,讨论了算法的全局收敛性，且给出了结合形如共轭梯度法FR,PR,HS的记忆梯度法的修正形式.数值实验表明,新算法比Armijo线搜索下的共轭梯度法FR、PR、HS和记忆梯度法更稳定、更有效.

无约束优化; 记忆梯度法; 广义Armijo线搜索; 全局收敛性

0 引言

考虑无约束优化问题

minf(x),x∈Rn,

(1)

文献[1]中提出一个算法类，其中搜索方向为：

(2)

文献[2-3]提出的算法中搜索方向dk及其参数βk的假设条件为

本文在文献[2-3]的理论基础上，对文献[1]的搜索方向dk中的参数βk给出了类似的假设，从而建立了求解问题(1)的一个新的记忆梯度算法，并在去掉迭代点列{xk}有界和广义Armijo步长搜索下,讨论了算法的全局收敛性.

1 算法及其性质

假设

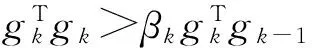
式中θk为gk和gk-1的夹角.

算法如下：

初始步:μ1,μ2∈(0,1),且μ1≤μ2；γ1,γ2>0；Δ>0为常数.

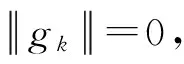
Step3ak满足广义Armijo搜索[3]：

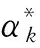
Step4xk+1=xk+αkdk,k=k+1,转Step1.

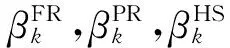
注3结合形如共轭梯度法FR,PR,HS的记忆梯度法和本文算法，可选取βk为:

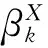
引理1若xk不是问题(1)的稳定点,则有

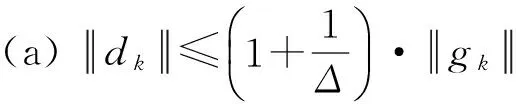
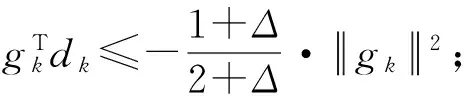
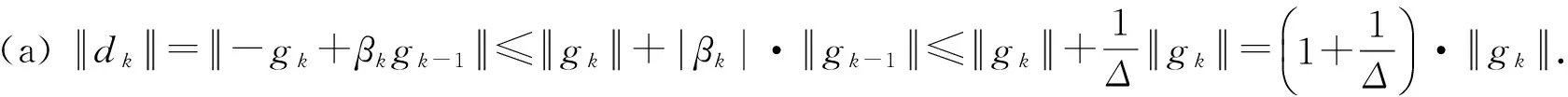
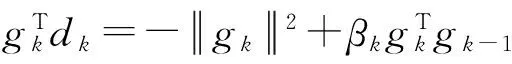
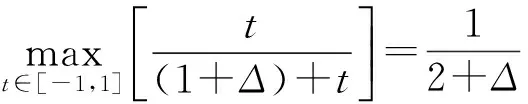
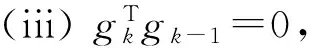
(c)证明可参考文献[2]中引理3.

2 算法全局收敛性

以下假设算法产生的点列{xk}为一无穷点列,全局收敛结果如下：

定理1假设f(xk)∈C1,则

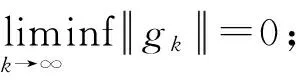
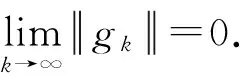
证明参考文献[3]中定理4的证明.

3 数值实验

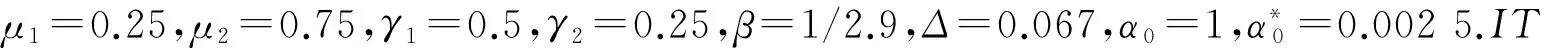
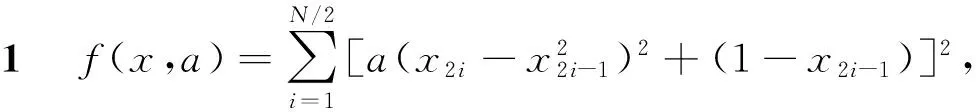
表1 例1的数据

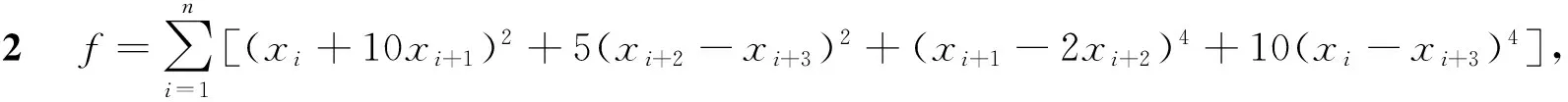
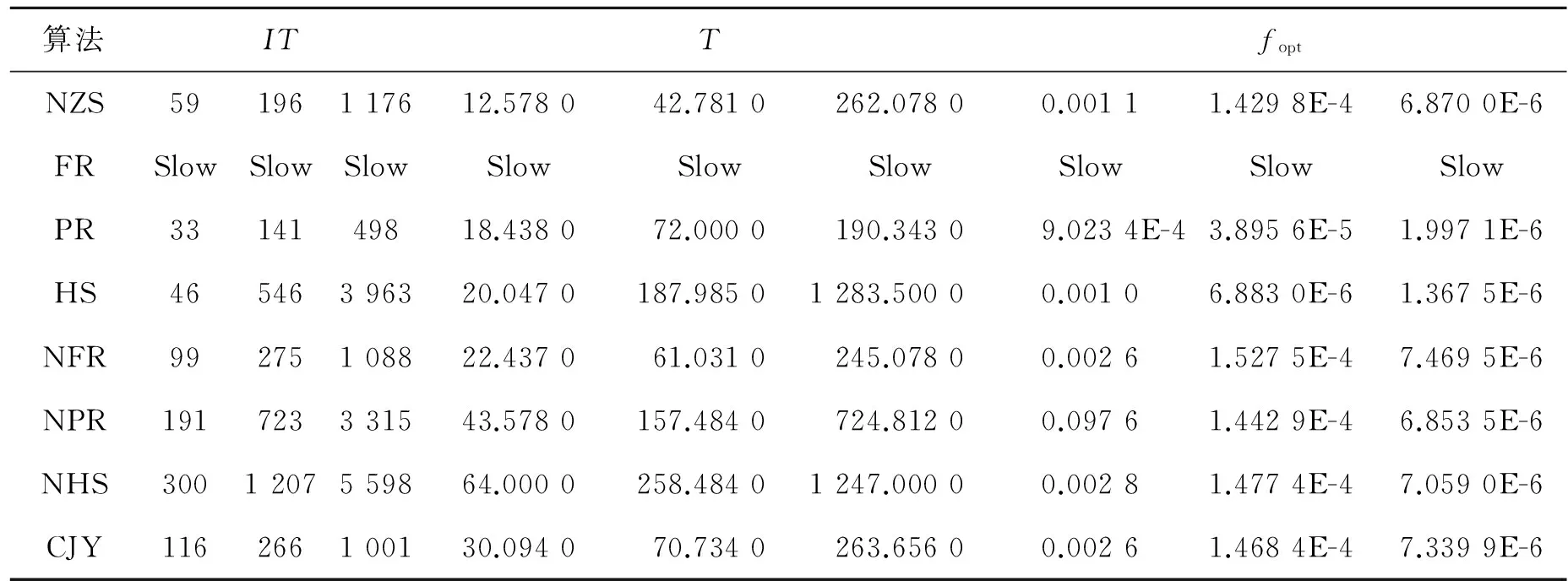
表2 例2的数据

从以上数值实验和比较可以看出，本文算法虽然有时不如其他算法，但是它不随函数改变而发生明显变化，即本算法收敛速度均匀，计算效能良好，适合求解大规模无约束优化问题.故本算法是有效的.

[1] 时贞军. 无约束优化的超记忆梯度算法[J]. 工程数学学报, 2000, 17(2): 99-104.

[2] 孙清滢,刘新海.结合Armijo步长搜索的一类新记忆梯度算法及其特征[J]. 石油大学学报, 2003, 27(5): 129-132.

[3] 孙清滢. 结合广义Armijo步长搜索的一类新的共轭梯度算法及其特征[J]. 工程数学学报, 2003, 20(1): 14-20.

[4] Shi Zhenjun. A new super-memory gradient method for unconstrained optimization[J]. 数学进展, 2006,35(3): 265-274.

AClassofMemoryGradientSearchAlgorithmwithGeneralizedArmijoStepSize

ZHU Shuai1, WANG Xi-yun2

(1.SchoolofEngineering,ShanxiDatongUniversity,Datong037003,China; 2.SchoolofAppliedScience,TaiyuanUniversityofTechnology,Taiyuan030024,China)

An assumed condition of parameters was given in the memory gradient directions to determine values that these parameters may take.The values range ensure the objective function was sufficient descent,and a new memory gradient algorithm was presented.The convergence was discussed without the generalized Armijo step size rule and the assumed condition that the sequence of iterates was bounded.Combing FR,PR,HS methods with the new method,the modified of the memory gradient algorithm was given.Numerical results showed that the new algorithm was more stable and efficient that conjugate gradient methods FR,PR,HS and Armijo step size rule.

unconstrained optimization；memory gradient method；generalized Armijo line search；global convergence

O 221.2

A

1671-6841(2011)03-0016-03

2010-07-18

山西省自然科学基金资助项目, 编号2008011013.

朱帅(1980-), 男, 讲师, 硕士, 主要从事最优化理论与方法研究, E-mail:sxdtdxzs@126.com; 通讯作者:王希云(1964-), 女, 教授, 主要从事最优化理论与方法研究, E-mail:tykdwxy@126.com.