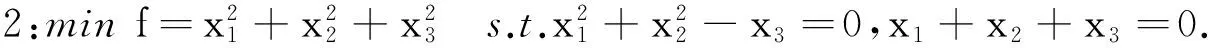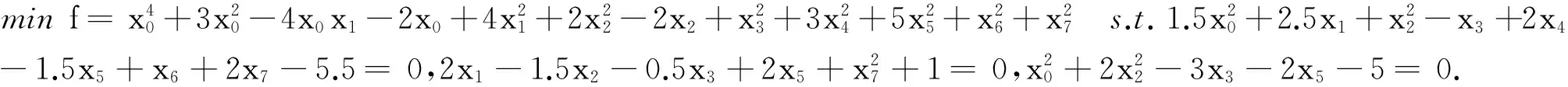非线性等式优化的一种非单调SQP滤子算法
2011-12-02王希云
王 珺,王希云
(太原科技大学 应用科学学院 山西 太原 030024)
非线性等式优化的一种非单调SQP滤子算法
王 珺,王希云
(太原科技大学 应用科学学院 山西 太原 030024)
SQP滤子方法是解非线性规划的一种较为有效的方法,但是滤子方法也会遇到Maratos效应.采用非单调技术来避免Maratos效应,并采用降维的Byrd和Omojokun方法来计算试探步.在一定条件下,给出了全局收敛性证明,数值试验表明该算法有效.
非线性等式约束; 信赖域; SQP; 滤子; 非单调
0 引言
非线性等式约束优化问题如下
(P):minf(x) s.t.ci(x)=0,i∈I={1,2,…,m},
其中,x∈Rn,f:Rn→R,ci:Rn→R,c(x)=(c1(x),c2(x),…,cm(x))T.
文[1]提出滤子的概念并将其应用于信赖域SQP方法后,信赖域SQP滤子方法就成为解决非线性规划问题的一种重要方法.但是,信赖域SQP滤子方法也会遇到Maratos效应.为避免Marotos效应,通常使用二阶校正步技术及非单调技术.
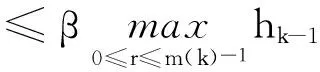
这种方法是有效的,但也存在不足,由于取当前迭代点及其前m(k)个点中函数值最大的fl(k)作为参考函数值,可能会在某些步中丢失更优点.
本文对上述算法进行了改进,提出一种非单调格式,并给出了求解非线性等式约束问题的非单调信赖域SQP滤子算法.对算法的适定性和全局收敛性进行了论证,并通过数值试验表明了算法的有效性.
1 算法

(1)
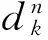
(2)

针对文[2,4-5]中算法的不足,本文采用非单调滤子形式:
(3)
(4)
当且仅当(3)式或(4)式成立时,当前迭代点xk+1可被过滤接受.
此外,我们定义如下参数:

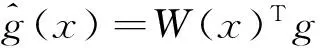
算法1如下:
step0初始化.给出初始点x0∈Rn,初始信赖域半径Δ0≥Δmin>0,初始对称矩阵H0∈Rn×n.初始化滤子F={
(h0,f0)
},令k=0,m(k)=0,0<γ<β<1,0<λ≤1,0 Step3测试试探步是否被算法接受. 计算h(xk+dk),f(xk+dk),如果xk+dk被滤子接受,转step4,否则转step5. Step5取Δk∈[r0Δk,r1Δk]≥Δmin,转step2. Step6令xk+1=xk+dk,更新滤子. 令Δk+1∈[Δk,r2Δk]≥Δmin,更新Hk,m(k+1)=min{m(k)+1,M},k=k+1,转Step1. 说明Hk的调节见文献[6],Wk的计算见文献[7]. 本文假设如下: A1对任意的k,xk和dk均属于有界闭凸集子集S⊂Rn; A2目标函数f(x)和约束函数c(x)(i∈I={1,2,…,m})在S内二次连续可微; A3对任意的k,Hk一致有界; 引理1[2]在假设条件成立时,存在不依赖于迭代的正常数α2,α3,使 定理1若假设成立,则算法是适定的.即算法中step1和step3、step5间的内循环会有限终止. 证明假设在迭代点xk处算法1中step1和step3、step5间的内循环不有限终止,则当k→∞时,Δk→0.下面分两种情况考虑. (5) 由式(5)可得,当Δk→0时有 (6) 由式(6)及过滤的定义可知,xk+dk被过滤接受.所以,当Δk→0时,算法1中step1和step3间的内循环终止. 证明若算法并不有限终止,则说明无穷的迭代点列{xk}被过滤接受.根据过滤的定义我们分以下两个部分来证明: 下面仅证明第(i)部分,关于第(ii)部分的证明可参考文献[2].记hk+1=h(xk+dk),分2种情形证明. 证毕. 由引理2、引理3可得定理2. 定理2若算法1产生的点列{xk}是一个无穷点列,那么{xk}的任一聚点是问题(P)的一个KKT点. 试验使用matlab软件来求解.取误差为10-4,并取各初值为: H0=I∈Rn×n,β=0.98,γ=0.02,ρ=0.5,α=δ=0.1,r0=0.1,r1=0.5,r2=2,Δmin=10-6,Δ0=1. 数值试验结果见表1.数值试验表明,本文算法是有效的. 表1 数值试验结果 [1] Fletcher R, Leyfer S.Nonlinear programming without a penalty function[J]. Mathematics and Statistics,2002,91(2):239-269. [2] Ke S,Dingguo P.A nonmonotone filter trust region method for nonlinear constrained optimization[J]. Journal of Computational and Applied Mathematics,2009,223(1):230-239. [3] 董纪昌,汪寿阳,薛毅,等.等式约束的一种降维运算的信赖域方法[J].中国管理科学, 2001, 9(6):26-30. [4] Fletcher R, Leyfer S, Toint P L.On the global convergence of a trust-region SQP-filter algorithm[J]. SIAM Journal on Optimization,2002,13(1):44-59. [5] Fletcher R, Gould N I M, Leyfer S, et al. Global convergence of a trust-region SQP-filter algorithm for general nonlinear programming[J].SIAM Journal on Optimization,2002,13(3):635-659. [6] Ulbrich S.On the superlinear local convergence of a filter-SQP method[J]. Math Program:Ser B, 2004,100(1):217-245. [7] Ulbrich M, Ulbrich S. Non-monotone trust region methods for nonlinear equality constrained optimization without a penalty function[J].Math Program:Ser B, 2003, 95(1):103-135. NonmonotoneSQPFilterMethodforNonlinearConstrainedEqualityOptimization WANG Jun, WANG Xi-yun (SchoolofAppliedSciences,TaiyuanUniversityofScienceandTechnology,Taiyuan030024,China) Nonlinear constrained optimization was efficient and robust solved by the SQP filter approach.But,the so-called Maratos effect was suffered.A non-monotone trust region method was presented. The step was computed by the Byrd and Omojokun scheme.Global convergence was proved under certain conditions. nonlinear equality constrained optimization; trust-region; SQP; filter; nonmonotone O 221.2 A 1671-6841(2011)03-0062-04 2010-02-08 山西省自然科学基金资助项目,编号2008011013. 王珺(1984-),女,硕士研究生,主要从事最优化理论研究,E-mail:simple_cloud@126.com.
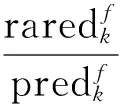


2 算法的适定性
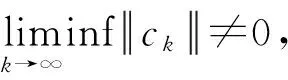


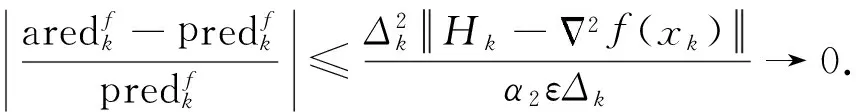
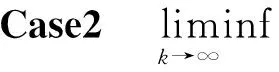
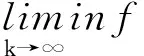
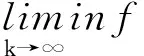
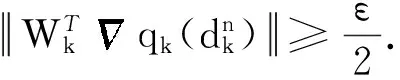
3 算法的收敛性

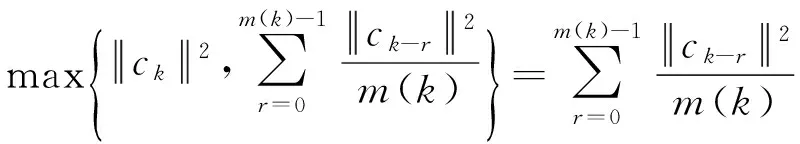
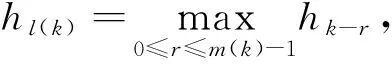

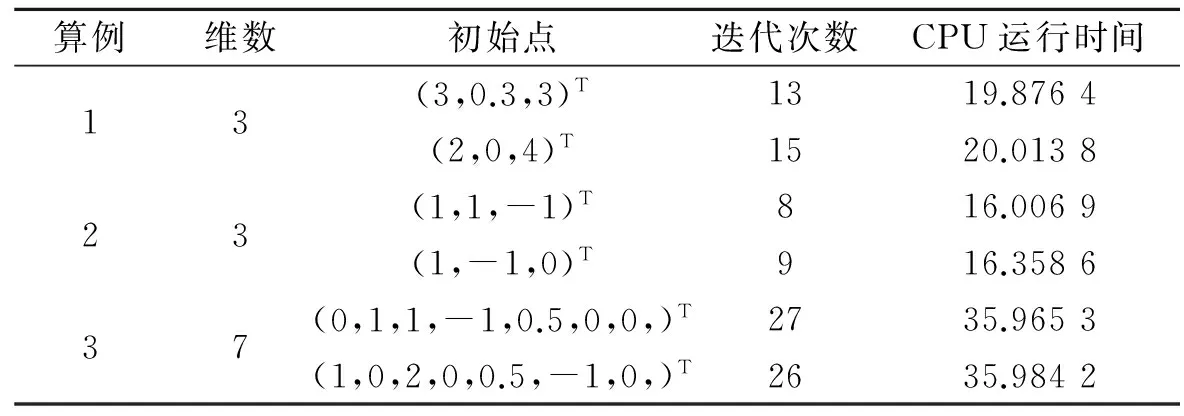
4 数值试验