基于LMI的随机时滞神经网络的全局渐近稳定性分析

杨红艳, 夏茂辉, 于 玲, 李海龙

(燕山大学 理学院 河北 秦皇岛 066004)

基于LMI的随机时滞神经网络的全局渐近稳定性分析

杨红艳, 夏茂辉, 于 玲, 李海龙

(燕山大学 理学院 河北 秦皇岛 066004)

研究了一类时变时滞与分布时滞的随机神经网络模型的全局渐近稳定性，该模型考虑了神经网络的随机扰动性.通过构造适当的Lyapunov泛函，以线性矩阵不等式的形式给出了系统全局渐近稳定的充分条件.最后，数值算例说明了结果的正确性.

随机神经网络； 分布时滞； 全局渐近稳定； Lyapunov 泛函

0 引言

神经网络是一种特殊结构的动力系统,已被成功地应用到很多领域,如信号处理、非线性代数微分方程的求解.由于神经网络系统常常受到随机因素的干扰以及系统本身存在延时, 所以出现了随机神经网络模型.近年来，对随机时滞神经网络全局稳定性的研究已取得了一些有益的成果[1-2].

到目前为止，时滞神经网络的大部分工作是处理带有分布时滞神经网络的稳定性问题，由于轴突的大小和长度的不同，以及并行通道的存在，神经网络具有空间的特性，所以描述神经网络的模型一般都引入没有界限的时滞.许多学者对带有分布时滞的随机神经网络有很大的研究兴趣.文献[3-4]研究了含有无界分布时滞神经网络的全局稳定性，然而随机性在模型中没有给于考虑.文献[5]虽然引用了分布时滞，但分布时滞是有界的.在[6-10]的基础上，研究了无界分布时滞的随机神经网络的全局渐近稳定性.通过构造适当的Lyapunov泛函，结合不等式技巧，以线性矩阵不等式的形式，建立了带有无界分布时滞的随机神经网络系统全局渐近稳定的新判据.

1 预备知识

考虑含有微分积分系统的连续时滞神经网络

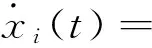
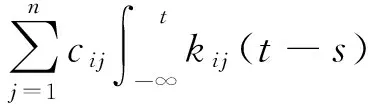
(1)

或者

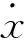
(2)

其中，i=1,2,…,n,n表示神经网络细胞的个数，xi(t)是时刻t第i个神经细胞的状态，x(t)=(x1(t),x2(t),…,xn(t))T∈Rn,(x(t))=[1(t),2(t),…,n(t)]T∈Rn在时刻t第j个神经细胞的激励函数，D=diag(d1,d2,…,dn)>0是正对角矩阵，A=(aij)n×n,B=(bij)n×n,C=(cij)n×n分别是反馈矩阵、时滞反馈矩阵和反馈矩阵，I=(I1,I2,…,In)T是外部输入向量，kij(s)在[0,+∞)→[0,+∞)连续有界且满足是任意非负连续函数，并且满足其中τ,u是已知常数.

要求每个fj(j=1,2,…,n)是有界的并且满足条件H.

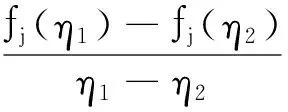
系统(1)的初始条件xi(t)=øi(t),t∈[-τ,0],i=1,2,…,n,其中øi(t)是定义在[-τ,0]上的连续函数.

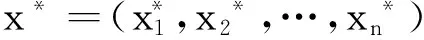
y(t)=x(t)-x*,y(t-τ(t))=x(t-τ(t))-x*,

则系统(2)变成以下形式

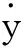
(3)

由假设H我们得知对于每一gj(·)都满足

H1gj(0)=0,

H2|gj(ζj)|≤Lj|ζj|,∀ζj∈R,

H3gj2(ζj)≤Ljζjgj(ζj),∀ζj∈R.

下面考虑如下一类带有时变时滞和分布时滞的随机神经网络

其中i=1,2,…,n;gj(yj)=j(yj+xj*)-gj(xj*);w(t)=(w1(t),w2(t),…,wn(t))T是定义在完备的概率空间(Ω,F,P)上具有{Ft}t≥0自然流的m维Brown运动，w(s):0≤w(s)≤t.σ(t,x,y):R+×R×R→Rn×m满足Lipschitz连续和线性增长条件，σ(t,x*(t),x*(t-τ(t)))=0.

2 主要结果

Θ=(u-1)Q1+P2

证明选择下面的Lyapunov 泛函

V(y(t),t)=V1(y(t),t)+V2(y(t),t)+V3(y(t),t)+V4(y(t),t);

其中,

V1(y(t),t)=yT(t)Py(t);

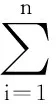
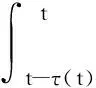
由此可以推出

LV(y(t),t)≤yT(t)[-2PD+P1+Q1]y(t)+2yT(t)PAg(y(t))+2yT(t)PBg(y(t-τ(t)))+

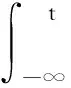
E)g(y(t))+2βgT(y(t))MBg(y(t-τ(t)))+

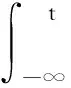
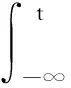
所以LV(y(t),t)≤ζT(t)Ξζ(t)+yT(t-τ(t))Θy(t-τ(t)).

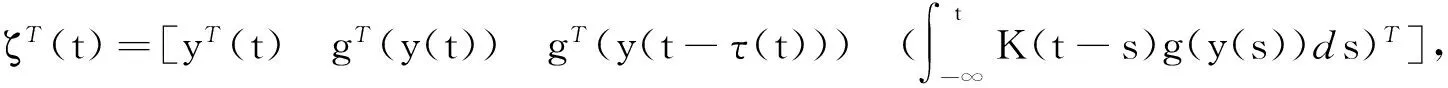
Θ=(u-1)Q1+P2,

因此，对于系统模型(4)在任何状态下保证LV(y(t),t)为负定的充分条件是Θ<0,Ξ<0,这就意味着系统(4)的平衡点是全局渐近稳定.

当定理1中β=1，易得到推论1.

推论1对于系统(4)，如果存在矩阵P=diag(pi)n×n>0,P1≥0,P2≥0,使得trace[σT(t,y(t),y(t-

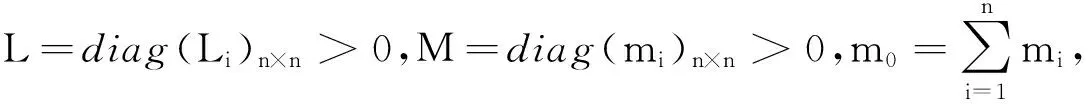
Θ=(u-1)Q1+P2

推论2对于系统(3),如果存在正定矩阵P,Q1,Q2，正定对角矩阵M,E，以及β>0满足Θ<0,Ξ<0，则系统(3)是全局渐近稳定.其中,

Θ=(u-1)Q1

3 数值算例

考虑随机无界分布时滞神经网络(4),并给出算例仿真实验.神经网络模型如下

dy1(t)=[-3y1(t)-g1(y1(t))+0.5g2(y2(t))-0.5g1(y1(t-τ(t)))+

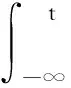
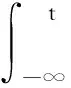
dy2(t)=[-4.5y2(t)+0.5g1(y1(t))-g2(y2(t))+0.1g1(y1(t-τ1(t)))-

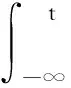
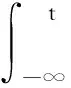
(5)

其中,激励函数gi(x)tanh(x),τ1(t)=0.6+0.5sint,τ2(t)=0.6+0.5cost,ki(t-s)=e-(t-s).时滞反馈矩阵A,B,C,D分别是

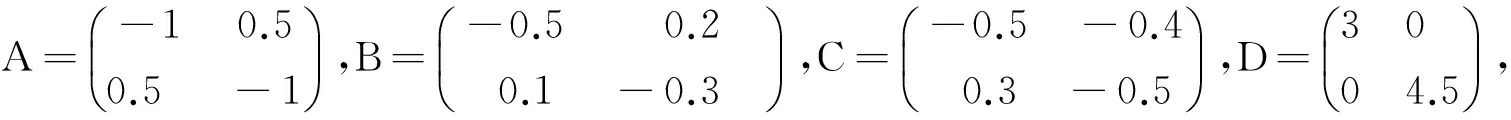
由定理1，应用matlab的LMI工具箱,可以得到系统模型(5)是全局渐近稳定的可行解

通过仿真图图1可以看出,系统模型(5)是全局渐近稳定的.

图1 随机神经网络的全局渐近稳定性

[1] Wan L, Sun J H．Mean square exponential stability of stochastic delayed Hopfield neural networks[J]. Phys Lett A, 2006, 343(4):306-318．

[2] Wang Z D, Shu H S, Fang J A, et al．Robust stability for stochastic delay Hopfield neural networks with time delays[J]．Nonlin Anal: Real World Appl, 2006,7(5):1119-1128．

[3] Ruan S G, Filfil R S. Dynamics of a two-neuron system with discrete and distributed delays[J]. Physica D: Nonlinear Phenomena,2004,191(3/4):323-342．

[4] Zhao H Y. Global asymptotic stability of Hopfield neural network involving distributed delays[J]. Neural Networks, 2004,17(1):47-53．

[5] Wang Z D, Liu Y R, Fraser K,et al．Stochastic stability of uncertain Hopfield neural networks with discrete and distributed delays[J]．Phys Lett A,2006,354 (4):288-297．

[6] 陈武华，卢小梅，李群宏．随机Hopfield 时滞神经网络的均方指数稳定性：LMI方法[J]．数学物理学报,2007,27A(1):109-117．

[7] 赵碧蓉，江明辉，沈铁．随机时滞神经网络的全局指数稳定性[J]. 控制理论与应用, 2005, 22(5):799-801．

[8] 冯伟,张伟, 吴海霞. 不确定随机离散分布时滞神经网络的鲁棒稳定性[J]. 计算机应用研究,2009,26(4):1222-1225.

[9] 刘德友, 张建华,关新平．基于LMI的时滞神经网路的全局渐近稳定性分析[J]．应用数学与力学,2008,29(6):735-740．

[10] 罗日才，许弘雷．随机变时滞神经网络的全局渐近稳定性[J]．通信技术, 2009,42(6):197-199．

GlobalAsymptoticStabilityAnalysisofClassofStochasticDelayNeuralNetworks

YANG Hong-yan，XIA Mao-hui，YU Ling，LI Hai-long

(SchoolofScience,YanshanUniversity,Qinhuangdao066004，China)

Global asymptotic stability for a class of stochastic neural networks with time-varying delays and distributed delay was studied. By constructing suitable Lyapunov functionals and combining with matrix inequality technique, a simple sufficient condition was presented for global asymptotic stability in the mean square of stochastic neural networks with time-varying delays and distributed delay. By LMI toobox, it demonstrated the usefulness of the new proposed global asymptotic stability criteria.

stochastic neural networks; distributed delay; global asymptotic stability; Lyapunov functionals

TP 183

A

1671-6841(2011)03-0048-05

2010-07-10

燕山大学博士基金资助项目，编号B272.

杨红艳(1982-),女，硕士研究生，主要从事神经网络的稳定性研究,E-mail:yanghongyan3190845@163.com；通讯作者：夏茂辉(1964-),男,教授,主要从事无网格方法研究,E-mail:zhizihua666@126.com.