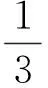B-D功能反应密度制约的离散非自治捕食者—食饵系统的周期解

李海银

(河南财经政法大学 数学与信息科学系 河南 郑州 450002)

B-D功能反应密度制约的离散非自治捕食者—食饵系统的周期解

李海银

(河南财经政法大学 数学与信息科学系 河南 郑州 450002)

利用Gains和Mawhin重合度理论中的延拓定理，得到了一类具有Beddington-DeAngelis功能反应密度制约的离散非自治捕食者—食饵系统周期解存在性的充分条件，推广了某些已知的相关结果.这个结论不仅适用于离散时滞，同样也适用于分布时滞和偏差变元.

捕食者密度制约； B-D功能反应函数； 周期解； 重合度理论； 延拓定理

0 引言

Beddington[1]和DeAngelis[2]分别提出了下面捕食者—食饵模型

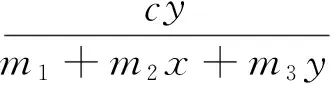
(1)

近年来很多专家研究发现，具有B-D功能反应的捕食者—食饵系统[3-7]的出生率、死亡率和其他重要的种群变化率都发生着很大的变化，因此，参数有周期性的假设和周期性的环境(比如天气的季节性影响，食物供应，交配习性等)是非常符合的.当把参数的周期性考虑进去时，模型(1)一定是非自治的. 文献[4]研究了非自治捕食—食饵动力系统

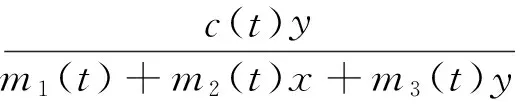
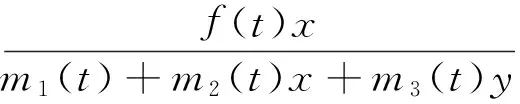
(2)

然而，许多学者[8-9]认为当种群不是世代重叠时，离散时滞的差分方程模型较连续的更适合，且一定的环境限定了捕食者应该是密度制约的[10-11]，下面讨论离散非自治模型的周期解

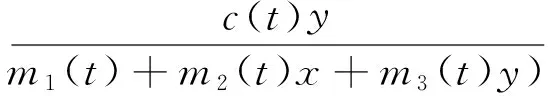
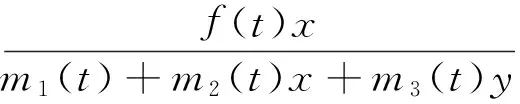
(3)

其中e(t)为捕食者的密度制约率.采用[12]中的方法，可推导出(3)的离散模型

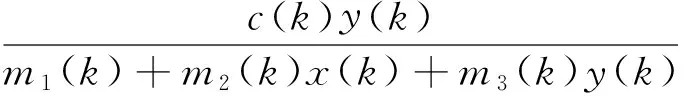
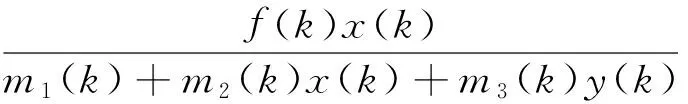
(4)

(4)的指数形式比(3)用差分形式代替微分在生物学上更合理，且连续时滞系统比离散时滞系统研究起来更难.下面将讨论系统(4)的正周期解的存在性以及存在的充分条件.

1 周期解

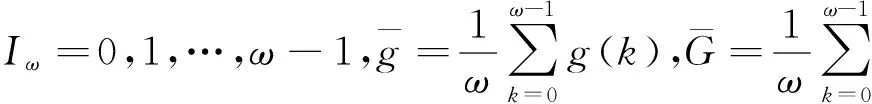
(i)对任意的λ∈(0,1)，方程Lx=λNx的解满足x∉∂Ω；

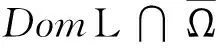
引理2已经在文献[13]中得以证明，这个引理将在先验估计和获得正周期解的一致有界方面起非常重要的作用.

引理2令f:Z→R是ω周期函数，则对固定的k1,k2∈Iω和k∈Z，有

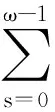
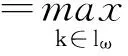
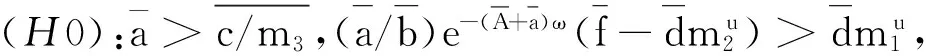
证明作变换x(t)=eu(t),y(t)=ev(t)和U=(u(t),v(t))T，则系统(4)等价于

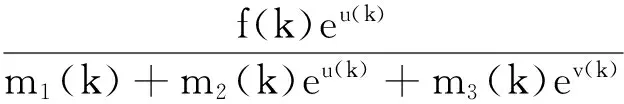
(5)

我们定义X=U=lω,(lf)(k)=f(k+1)-f(k)，则

对任意的f∈X和k∈Z,我们很容易得到L是一个有界的线性算子，且KerL=lcω，ImL=l0ω,dim KerL=2=codim ImL,则L是一个零指标的Fredholm映射.令

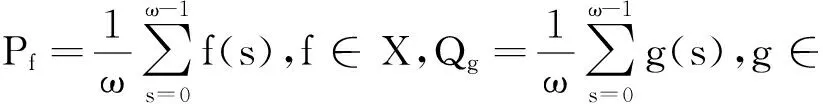
很明显，P和Q是连续映射，使得ImP=KerL,ImL=KerQ=Im(I-Q)且存在

KP∶ImL→KerP∩DomL,

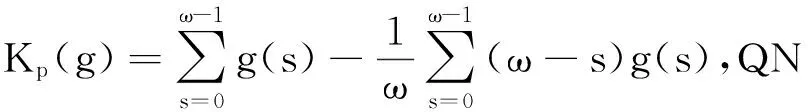
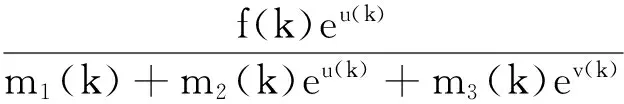
(6)

如果U是系统(6)的任意解，我们有

这意味着

(7)

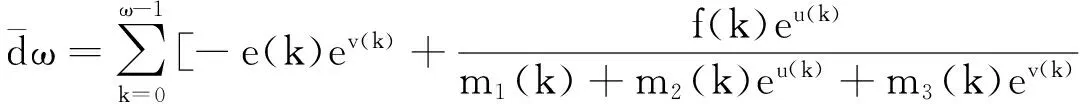
(8)

结合(6)～(8), 我们有

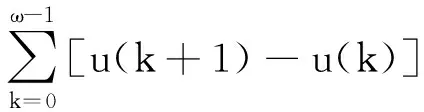
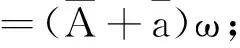
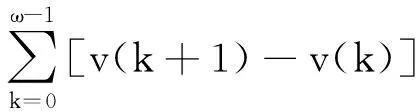
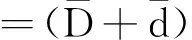
(9)

由于U=U(k)∈X，一定存在ξi,ηi∈Iω,i=1,2使得

(10)

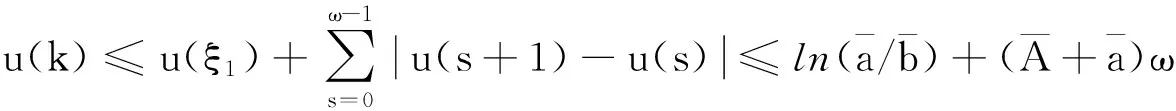
(11)

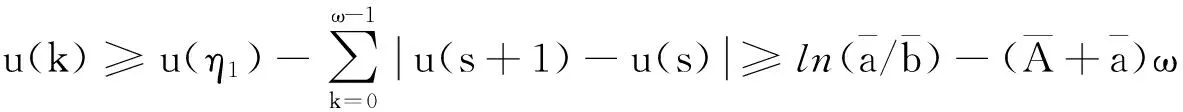
(12)

结合(11)，则

|u(k)|≤max{|A1|,|A2|}∶=C1.

(13)

由(7)、(10)和(11)，得

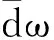
从上面可以得出，

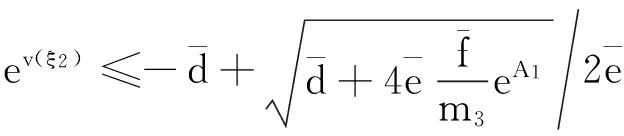
(14)

由引理2及等式(9)和(14)，得

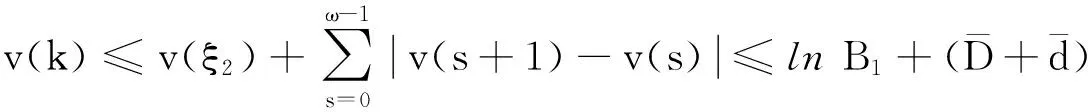
由(7)和(12)，容易得到

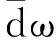
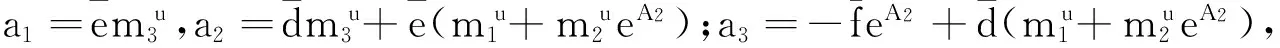
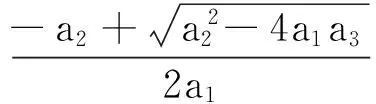
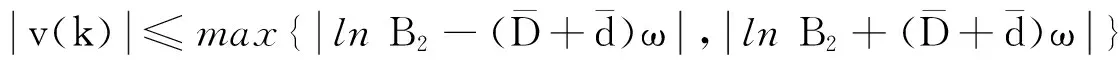
(15)

且|(ln{s1*},ln{s2*}|

k∈Z.令Ω∶={U={U(k)}∈X:‖U‖

因代数方程组(15)存在惟一解，由已知条件直接计算知deg(JQN,Ω∩KerL,0)≠0，这里同构J可取为恒同映射，因为ImQ=KerL.至此，我们已经证明Ω满足引理1的全部条件.由引理1，方程(5)在DomL∩Ω中至少存在一个ω周期解U*={U*(k)}={(u*(k),v*(k))T}，令x*(k)=eu*(k),y*(k)=ev*(k)，则X*={X*(k)}={(x*(k),y*(k))T}是系统(4)的ω周期正解，存在正常数αi,βi满足上面的讨论.证毕.

例1令

e(t)是任意的连续正ω周期函数，且令ω=4，通过简单的数值计算，可得

因此，系数函数满足条件H0，系统至少有一个 正周期解.

注1从定理1 可以看出，只要满足条件H0，条件H0和正的连续ω周期函数e(t)的取值无关，系统(4)至少有一个ω正周期解.也就是说，捕食者的密度制约比率e(t)对周期解的存在性不存在任何负作用.

注2当系统(4)的部分或全部项换为离散时滞、分布时滞或偏差变元时，定理1仍然是成立的.

[1] Beddington J R. Mutual interference between parasites or predators and its effect on searching efficiency[J].J Animal Ecol,1975,44(1):331-340.

[2] DeAngelis D L, Goldstein R A, O′Neil R V.A model for trophic interaction[J].Ecology,1975,56(4):881-892.

[3] Cui Jing’an, Takeuchi Y. Permanence, extinction and periodic solution of predator-prey system with Beddington-DeAngelis functional response[J]. J Math Anal Appl,2006,317(2):464-474.

[4] Fan Meng，Kuang Y. Dynamics of a nonautonomous predator-prey system with the Beddington-DeAngelis functional response[J].J Math Anal Appl,2004,295(1):15-39.

[5] Liu Shengqiang, Beretta E. A stage-structured predator-prey model of Beddington-DeAngelis type[J]. SIAM J Appl Math, 2006,66(4):1101-1129.

[6] Hwang T W. Global analysis of the predator-prey system with Beddington-DeAngelis functional response[J]. J Math Anal Appl, 2003,281(1):395-401.

[7] Cantrell R S, Cosner C. On the dynamics of predator-prey models with the Beddington-DeAngelis functional response[J]. J Math Anal Appl, 2001,257(1):206-222.

[8] May R M. Stability and Complexity in Model Ecosystems[M].Princeton:Princeton Univ Press,1974.

[9] Freedman H I. Deterministic mathematical models in population ecology[M].New York:Marcel Dekker,1980.

[10] Li Haiyin, Takeuchi Y. Dynamics of the density dependent predator-prey system with Beddington-DeAngelis functional response[J]. J Math Anal Appl, 2011,374(2):644-654.

[11] Li Haiyin, Takeuchi Y.Stability of ratio-dependent predator-prey system with density dependence [C]// Proceedings of the 7th conference of Biological Dynamic System and Stability of Differential Equation.New York:World Academic Press,2010:144-147.

[13] Gaines R E, Mawhin R M. Coincidence Degree and Nonlinear Differential Equations[M].Berlin:Springer-Verlag,1977.

[12] Fan Meng,Wang Ke. Periodic solutions of a discrete time nonautonomous ratio-dependent predator-prey system[J]. Mathematical and Computer Modelling,2002,35(9/10):951-961.

PeriodicSolutionofDiscreteTimeNonautonomousDensityDependentPredator-PreySystemwithB-DFunctionalResponse

LI Hai-yin

(DepartmentofMathematicsandInformation,HenanUniversityofEconomicsandLaw,Zhengzhou450002,China)

By using the continution theorem based on Gaines and Mawhin’s coincidence degree, sufficient and realistic conditions were obtained for the existence of positive periodic solutions for a discrete time nonautonomous density dependence predator-prey system with Beddington-DeAngelis functional response, and the results were improved.The results were applicable to distribute delays and deviating arguments.

density dependent predator; Beddington-DeAngelis functional response; periodic solution; coincidence degree; continution theorem

O 29

A

1671-6841(2011)03-0038-05

2010-09-09

国家自然科学基金资助项目，编号60774041.

李海银(1977-)，女，讲师，硕士，主要从事微分方程稳定性研究.E-mail:haiyinli2002@yahoo.com.cn