延迟产品分化的离散时间排队模型
2011-12-02宁小虎田乃硕原小娟徐利花
宁小虎,田乃硕,原小娟,赵 媛,徐利花
(燕山大学 理学院 河北 秦皇岛 066004)
延迟产品分化的离散时间排队模型
宁小虎,田乃硕,原小娟,赵 媛,徐利花
(燕山大学 理学院 河北 秦皇岛 066004)
研究了一个延迟产品分化的生产系统,供应商在MTS系统的基础上为制造商提供半成品,当收到客户订单时,制造商再在MTO系统的基础上通过定制半成品来满足客户的需求.供应商生产半成品所花费的时间占总生产时间的比例将决定半成品适应客户需求的程度,制造商希望决定最佳的产品分化点和半成品缓冲区大小.利用拟生灭过程和矩阵几何解得到这个系统的性能指标,并且给出优化策略,通过系统仿真得到优化结果.
延迟产品分化; 分化点; 半成品缓冲区; 拟生灭过程; 矩阵几何解
0 引言
在当今市场经济中,制造商们都采用两种策略来满足客户的需求:一是资源型模式(make-to-stock,MTS系统),这种系统虽然能在短时间内满足客户的订单需求,但是,由于产品生命周期短、需求多样化等原因会使库存风险增大;二是订单型模式(make-to-order,MTO系统),这种系统可以满足客户多样化的订单需求,并且有较小的库存风险,但是,它需要一个较长的产品交货时间.而延迟产品分化模式(delayed-product-differentiation,DPD系统)是一种混合型的策略,产品的一部分是通过MTS系统完成的,当一个客户订单到来时,制造商再通过MTO系统来完成整个产品.与MTS和MTO系统相比,这种系统可以缩短产品的交货时间和保持一个适度容量的库存,并且能够增强企业对于市场变化的适应性.然而,在实施的过程中,它会引起潜在费用的增加,同时使得满足客户需求的情况复杂化.
文[1-2]分析了库存费用和重新设计流程费用的优化问题,文[3]则构造了一个普通的排队模型来分析MTS、MTO和DPD系统,并测试了在多重排队系统中的最佳分化点.最近,文[4]对DPD系统做了进一步研究,在模型中加入市场特征,并用一个连续时间排队模型分析了DPD系统对客户延迟服务和库存风险的影响程度.然而,至今还没有利用离散时间排队模型研究DPD系统的报道.本文将建立一个离散时间排队模型来评估DPD系统的性能指标,并测试最佳的分化点和半成品缓冲区大小.与以往的研究相比,离散时间排队模型的应用更符合生产系统的实际情况,而且在库存优化管理及成本节约等方面有很大的改进.
1 模型描述
我们考虑DPD系统,该模型可以描述为:

2)设供应商拥有无穷的原材料并且为制造商提供相同的半成品,而制造商却有一个受限制的半成品库存容量k.客户到来时,如果库存中有半成品则直接开始服务,若库存中没有半成品则需等待直到供应商提供半成品后才开始服务.当制造商的库存量为k时,供应商不再提供半成品,只有当制造商的库存量不足k时,供应商才提供半成品,且供货只发生在时刻n-上.

4)当产品的大部分由供应商完成时,则最终产品很可能不太符合客户的订单需求,因此,设φ是半成品不符合客户需求的可能性,那么φ的值可以被认为是产品市场的一个特性,φ的值大表明客户对完工产品的满意度很低,而φ的值小则表明客户对完工产品的满意度很高.因为φ随θ单调递增,所以φ可以有一系列的数字表示,如φ=dθn,n≥1,0 5)假设到达间隔与服务时间相互独立且模型服从先到先服务的排队规则. 其中,B,C,A0,A1,A2都是(k+1)×(k+1)的矩阵. 2.1稳态条件 令A=A0+A1+A2,则 那么A是k+1阶的随机阵.设x={x0,x1,…,xk}是A的平稳概率向量,则x满足 xA=x,xe=1, (1) 2.2稳态分布和性能指标 其中R称为率阵,因为它的精确计算过程十分复杂,所以我们采用数值迭代算法来近似计算率阵R,其中迭代公式为Rn+1=A0(I-A1-RnA2)-1,n≥0,取初值R0=0,利用这一迭代公式就可以求出率阵R,即Rn收敛于R,然后通过|Rn+1-Rn|ij<10-3检验近似计算率阵R的精度.最后我们得到了以下的系统稳态性能指标: 1)系统中客户等待平均队长E(L)=π1(I-R)-2e. E(L)=X′(1)=π1(I-R)-2e. 3)系统中半成品平均数量E(S)=π0(I-R)-1V,V=[0,1,2,…,k]T. 为了更好地理解DPD系统,我们举例说明实现客户订单所需延迟平均时间E(W)、半成品平均数量E(S)和单位时间内不适合的半成品平均数量E(U)随k和θ的变化情况,所得结果将用matlab作图验证.给定系统的参数值:λ=0.25,μ=0.3,φ=0.5θ,δ=θ. 图1中,当θ的值比较小时,实现客户订单所需的延迟比较大.这是因为,尽管供应商提供了充足的、合适的半成品,但是产品的大部分是由制造商完成的,最终的产品不可能很快地满足客户的需求.随着θ值的增大,则产品的大部分工作由供应商来完成,这时尽管供应商的供应率在减小,不适合产品率也在增加,但是这样的损失会被制造商很高的客户服务率所弥补,所以,这时实现客户订单所需的延迟会减小.在θ的变化范围内,k值增大对实现客户订单所需的延迟没有显著影响,这就是离散时间排队模型较于以往研究的优势,制造商的库存只要保持一个适度的量,就可以在一定程度上实现减少客户订单所需延迟的目标.对于一个给定的θ,随着k的增加,单位时间内不适合半成品的平均数量在增加(见图2).当θ逐渐增加时,供应商提供的合适的半成品数量也在减少,这影响到了图3的半成品库存量. 一个基于排队模型的DPD系统不仅表明了θ和k的相互关系,而且要求制造商必须在有多少工作应由供应商完成和半成品缓冲区应有多大之间找到一个平衡,以使实现客户订单所需的延迟最小. 下面举例说明TC(θ,k)是如何随θ和k变化的.假设Ch=Cw=Cu=Cc=1.0,V(θ)=10θ,λ=0.25,μ=0.3,φ=0.5θ,δ=θ,τ=0.05,0<θ<1,k=0,1,….由图4可以得到最佳的分化点和半成品缓冲区大小是(θ*,k*)=(0.418,2),制造商花费的最少的总成本费用是TC(θ*,k*)=9.141 5. 图1 系统中实现客户订单所需延迟平均时间Fig.1 Expected customer order fulfillment delay 图2 单位时间不适合半成品的平均数量Fig.2 Expected number of unsuitable items produced per unit time 图3 系统中半成品平均数量Fig.3 Expected semi-finished goods inventory 图4 制造商花费的总成本Fig.4 TC(θ,k)for various k 本文建立优化模型来帮助我们理解延迟产品分化是如何影响客户延迟和库存风险的,并利用一个排队模型来研究不同参数变化下DPD系统的性能指标,最终测试了最佳的分化点和半成品缓冲区大小.DPD系统的研究是有意义的,因为敏感客户是如何定义完工产品,什么样的需求水平是客户可以接受的,供应商提供合适产品的能力如何等等这些问题对于制造商而言都是值得考虑的. [1] Aviv Y,Federgruen A.Design for postponement:a comprehensive characterization of its benefits under unknown demand distribution[J].Operations Research, 2001, 49 (4):578-598. [2] Aviv Y, Federgruen A.Capacitated multi-item inventory systems with random and seasonally fluctuating demands:Implications for postponement strategies[J].Management Science, 2001, 47 (4):512-531. [3] Gupta D, Benjaafar S.Make-to-order,make-to-stock, or delay product differentiation?A common framework for modeling and analysis[J].IIE Transactions, 2004, 36(6):529-546. [4] Elizabeth M J, Attahiru S A.A queueing model of delayed product differentiation[J].European Journal of Operation Research, 2009,199(3):734-743. [5] 田乃硕, 徐秀丽, 马占友.离散时间排队论[M].北京:科学出版社, 2008:141-147. [6] Li Jihong, Tian Naishuo.Analysis of the discrete time Geo/Geo/1 queue with single working vacation[J].Quality Technology and Quantitative Management, 2008, 5(1):77-89. [7] Tian N S, Zhang Z G.A two threshold vacation policy in multiserver queueing systems[J].European Journal of Operational Research, 2006,168 (1):153-163. [8] Liu Wenyuan,Xu Xiuli,Tian Naishuo.Stochastic decompositions in theM/M/1 queue with working vacations[J].Operation Research Letters, 2007,35 (5):595-600. [9] 田乃硕.休假随机服务系统 [M].北京:北京大学出版社, 2001:256-320. DiscreteTimeQueueingModelofDelayedProductDifferentiation NING Xiao-hu, TIAN Nai-shuo, YUAN Xiao-juan, ZHAO Yuan, XU Li-hua (SchoolofScience,YanshanUniversity,Qinhuangdao066004,China) A production system of delayed product differentiation was studied. The supplier produced semi-finished items on the MTS basis for a manufacturer that would customize the items on a MTO basis after a customer order was placed.The proportion of total processing time undertaken by the supplier determined how suitable the semi-finished items met the customer demand.The manufacturer needed to determine the optimal point of differentiation and its optimal semi-finished goods buffer size.Various performance measures for this system were evaluated by using the quasi birth and death process and matrix geometric solution. A strategy was designed to optimize the system, and the optimization results were got by system simulation. delayed product differentiation; point of differentiation; semi-finished goods buffer size; quasi birth and death process; matrix geometric solution O 226 A 1671-6841(2011)03-0011-05 2010-06-04 国家自然科学基金资助项目,编号10671170. 宁小虎(1986-),男, 硕士研究生, 主要从事排队论研究,E-mail:xiaohu134@163.com.2 模型分析







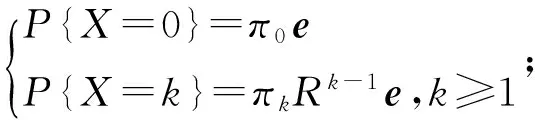


3 数值算例
4 制造商的最佳选择问题





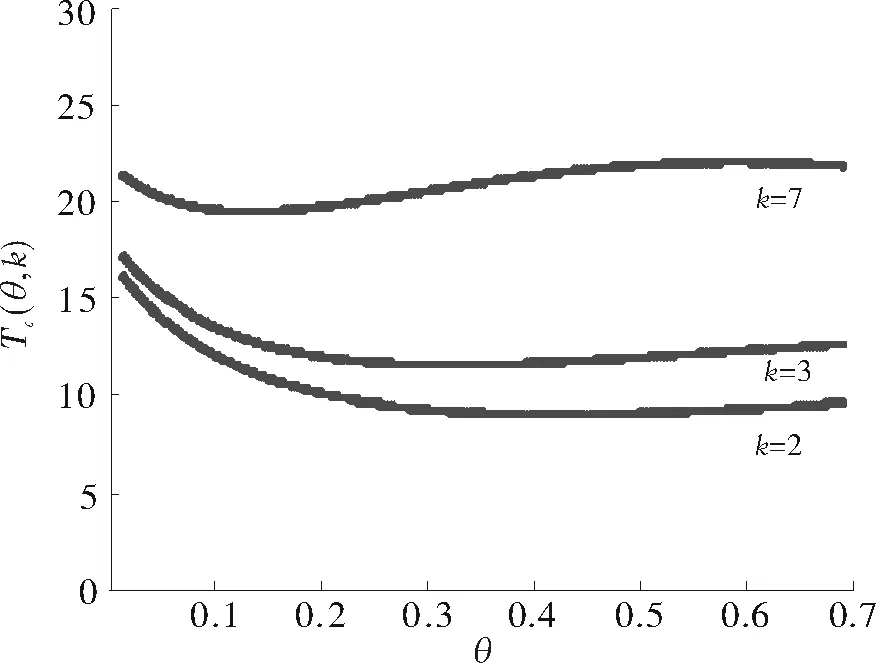
5 结束语
