带单重工作休假和休假中断的M/G/1排队系统
2011-12-02卢国云徐秀丽王继利刘春平
卢国云,徐秀丽,王继利,刘春平
(燕山大学 理学院 河北 秦皇岛 066004)
带单重工作休假和休假中断的M/G/1排队系统
卢国云,徐秀丽,王继利,刘春平
(燕山大学 理学院 河北 秦皇岛 066004)
研究单重工作休假和休假中断的M/G/1排队系统,得到了其嵌入Markov链的转移概率矩阵,采用M/G/1型结构矩阵解析法,得到离去时刻稳态队长的母函数的解析表达式.采用经典随机分解方法,给出了队长的条件随机分解结构、条件等待时间的随机分解结果、稳态等待时间的LST变换及稳态下平均等待时间等性能指标.给出数值例子,并讨论了系统参数对几个主要性能指标的影响,从而验证了理论分析的合理性和有效性.
单重工作休假; 休假中断;M/G/1型矩阵; 随机分解
0 引言
现实生活中有很多休假排队,在休假时服务员不是完全停止工作,而是以一个比正常服务率相对低一些的服务率工作,这样的休假制度称为工作休假.目前工作休假排队系统,是国内外专家研究的重点[1-3].文献[4]提出了休假中断策略,考虑了具有离散时间的GI/Geo/1的多种工作休假及休假终止模型.
目前,研究单重工作休假排队模型的不多,本文研究的是带有单重工作休假和休假中断策略的M/G/1排队系统.当系统处于休假期,一旦有新顾客到达,以低速服务顾客,顾客离去后仍有顾客,则休假中断,回到正常工作期,以高速率服务其他顾客.它的应用背景在于设置了低速运行期,从而减少运营成本降低能源消耗,考虑了休假中断策略,增强了系统的应急能力,而且在多重工作休假的基础上,缩短了休假时间,增加了系统闲期,以便接待随时到达的顾客,提高系统收益和顾客满意率.此外,本文使用随机分解理论给出了带单重工作休假和休假中断排队的M/G/1排队及经典休假M/G/1排队的关系,丰富了工作休假排队理论.
1 模型描述与嵌入Markov链
在一个到达率为λ服务率为μb的经典M/G/1排队系统中,同时引入单重工作休假和休假中断策略.当一次服务完成,系统变空时,服务员开始长度为V的休假,V服从参数为θ的指数分布.如果在休假期内有顾客到达,服务员将以服务率μv接待顾客,而非完全停止服务.当休假期间的一个顾客服务完成,系统中仍有顾客,则服务员立即结束休假,以正常速率μb(μv<μb)服务其他顾客,即休假中断发生,否则服务员继续休假.同时,若休假结束系统中无顾客,服务员进入通常的闲期,直到有新顾客到达,以服务率μb开始一个正规忙期.此模型记为M/G/1(SWV,VI)模型,模型描述如下:

2)休假期间内的服务时间Sv独立同分布, 具有一般分布函数Gv(x),且设LST变换,均值和k阶矩分别为:
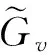
3)假设到达时间间隔、工作休假时间、正常服务期内的服务时间和工作休假期内的服务时间彼此独立,且遵循FCFO的服务规则.



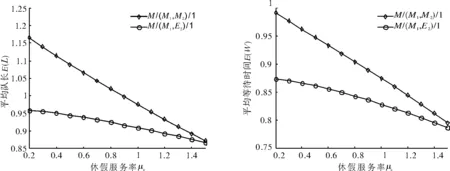
其中,bk(dk)表示V>Sv(V=Sv),且在一次休假服务时间Sv内到达k个顾客的概率;vk表示V 因此,{bk,k≥0},{vk,k≥0}和{dk,k≥0}是不完全概率分布,且有 显然, 为考虑状态0向其他状态转移的情况,引入记号α,α=P{V>T},其中T表示到达间隔. 首先,考虑第n次顾客离去后瞬间系统中有顾客,则其转移情况同无休假M/G/1排队,有 P{Ln=m-1+j|Ln=m}=aj,j≥0,m≥1. 下面考虑状态0的转移情况 当V>T时,有3种情况造成离去时刻从状态0转移到j:(i)V>Sv,且在一次休假服务时间Sv内到达j个顾客;(ii)V 当V P{Ln=j|Ln=0}=(1-α)aj+α(bj+cj+dj),j≥0. (1) 下面给出稳态队长的母函数. 定理1当ρ<1时,离去时刻的稳态队长的母函数为 L(z)=K(1-ρ){z[(1-α)A(z)+α(B(z)+C(z)+D(z))]-A(z)}/[z-A(z)], (2) 证明对πk(k≥0)取母函数,且由(1)式有 进而得 L(z)=π0{z[(1-α)A(z)+α(B(z)+C(z)+D(z))]-A(z)}/[z-A(z)]. (3) 由正规化条件L(1)=1,可得 将π0代入(3)式,引入记号K,定理得证. 定理2若ρ<1,离去时刻稳态队长L可以分解成两个随机变量之和L=L0+Ld,其中L0为经典M/G/1排队在离去时刻的稳态队长,附加队长Ld的母函数表达式为Ld(z)=[1-Ψ(z)]/[Ψ′(1)(1-z)],其中, Ψ(z)=z[(1-α)A(z)+α(B(z)+C(z)+D(z))]/A(z). 定义S=0或1,取决于任一顾客以休假服务率服务完成或正常速率服务完成,在下面的稳态等待时间随机分解中,将用到处于这两种状态的概率,因此,我们给出 Pb=P{S=1}=1-Pv 当顾客以正常服务速率服务完成时,剩余顾客即为此顾客等待时间Wb和正常服务时间Sb到达的顾客.因此,有 (4) 由条件概率可得 因此,任一顾客的稳态等待时间W的LST变换为: 图1 M/(M1,M2)/1(SWV,VI)系统中E(L)随μv的变化趋势Fig.1 The curves of E(L)with the change of μv in the M/(M1,M2)/1(SWV,VI)model 通过分析,我们得到了平均稳态队长、平均等待时间的表达式.对于不同的系统,参数不同.当然,改变参数,例如降低服务速率μv,就会影响模型的队长、等待时间等.所以,我们给出一些具体情况下的数值例子来说明模型可以有效地代表一些实际问题. 从图1可看出,在3种不同的休假率θ下,平均队长随休假服务率μv的增大而减小;固定μv及其他特征,平均队长随θ的增大而减小,这是符合实际情形的. 而在实际问题中,为使系统性能更好,需选用不同的休假策略,在此,以两种模型M/(M1,M2)/1(SWV,VI)和M/(M1,E2)/1(SWV,VI)对比,由图2形象的给出了休假服务率μv对平均队长及平均等待时间的影响. 图2 不同模型的对比Fig.2 The comparison of different models 从图2中可以分析出增大休假服务率μv,可以减少系统中聚集的顾客数以及等待时间,节省资源,达到充分利用的目的,同时给出了服从不同时间分布的平均队长的对比.例子说明,根据实际情形,设置不同的休假策略,再适当改变μv,ρ(θ)的值,可以使系统性能提升. [1] 田乃硕.休假随机服务系统[M].北京:北京大学出版社,2001:148-165. [2] Servi L D, Finn S G.M/M/1 queue with working vacations (M/M/1/WV)[J].Perform Evaluation,2002, 50(1):41-52. [3] Wu D,Takagi H.M/G/1 queue with multiple working vacations[J].Perform Evaluation,2006,63(7):654-681. [4] Li Jihong,Tian Naishuo.The discrete-time GI/Geo/1 queue with working vacation and vacation interruption[J].Applied Mathematics and Computation,2007,185(1):1-10. [5] Neuts M.Matrix-Geometric Solutions in Stochastic Models[M].Baltimore:Johns Hopkins University Press, 1981:40-65. [6] Shanthikumar T.On stochastic decomposition inM/G/1 type queues with generalized server vacations[J].Oper Res,1988,36(4):566-569. M/G/1QueuewithSingleWorkingVacationandVacationInterruption LU Guo-yun, XU Xiu-li, WANG Ji-li, LIU Chun-ping (CollegeofScience,YanshanUniversity,Qinhuangdao066004,China) AnM/G/1 queue system with a single working vacation and working interruption was studied.AnM/G/1-type transition probability matrix of the embedded Markov chain was obtained.And using theM/G/1-type matrix analysis method, the PGF of the stationary queue length for the customers at departure epochs was derived.By the classic stochastic decomposition solution, the stochastic decomposition results of the stationary queue length and the conditional waiting time were presented.And some performance measures of the system such as the LST of the stationary waiting time and the expected waiting time were also obtained.Numerical examples were presented to show the influence of the system parametes on several main performance characteristics,and the rationality and the effectiveness of the theoretical analysis were proved. single working vacation; vacation interruption;M/G/1-type matrix; stochastic decomposition O 226 A 1671-6841(2011)03-0006-05 2010-05-31 国家自然科学基金资助项目,编号10671170;河北省自然科学基金资助项目,编号F2008000864. 卢国云(1984-),女,硕士研究生,主要从事排队论研究,E-mail:luguoyun114@126.com.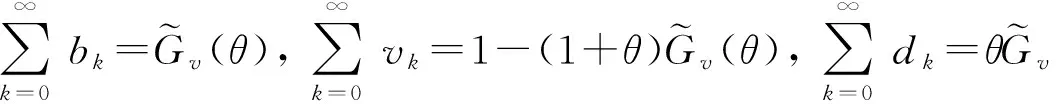
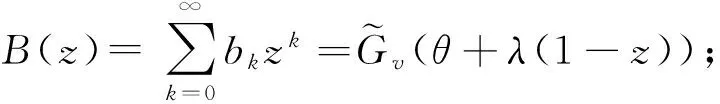




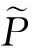
2 稳态队长及随机分解

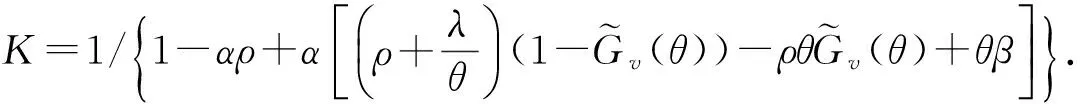



3 等待时间的随机分解

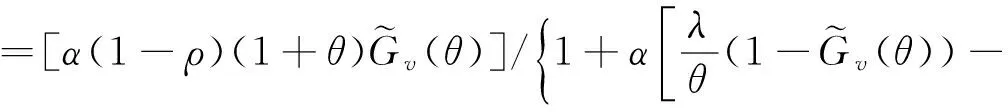




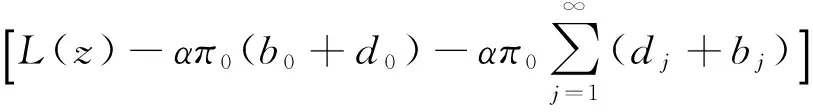


4 数值例子