RPROP神经网络的电力系统谐波分析

李 鹏

(云南省电力设计院，云南 昆明 650011)

0 引言

目前，由于人工神经网络具有自适应以及自学习的能力，因而在在电力系统谐波分析中的应用越来越广泛［1］.宁微微［2］等人将基于傅立叶基函数神经网络算法运用到电力系统的谐波分析中.李自成［3］等人对一种神经元自适应谐波电流检测方法进行了数字仿真研究.柴旭峥［4］等采用Adaline神经元算法进行了电力系统谐波分析研究，该算法缺点在于精度不高，并且实时性不强.向东阳［5］等人将汉宁窗插值算法用于电力系统谐波分析中，能够有效检测出非整数次的谐波，然而该算法的缺点在于受到步长以及动量项的影响较大.一般而言，步长以及动量项对电力系统谐波分析的精度和速度至关重要，步长以及动量项需要多次选择才能够取得其最优值.为此，本文提出了一种基于RPROP神经网络［6］的电力系统谐波分析算法.该算法能够提高网络的收敛速度，并且根据一种快速的加汉宁窗插值算法来取得网络的初值.经过验证，该算法的精度较高，并且不仅能分析整数次谐波，还能分析分数次谐波.

1 基于BP神经网络的谐波分析算法

对于含有分数次的谐波电力系统信号，其表达式如下所示:

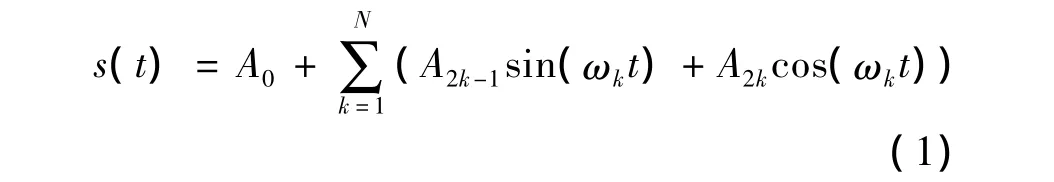
其中:A0—直流分量;

A2k－1—第k次谐波的正弦分量幅值;

A2k—第k次谐波的余弦分量幅值;

ωk—角频率.

假设神经网络的输出为函数X(i)，将信号函数s(t)以及时间t分别离散化处理为S(i)和T(i).因此，神经网络的结构可见图1.

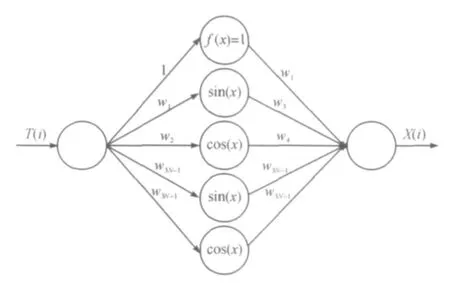
图1 神经网络结构模型图

神经网络的输出为函数X(i)，其表达式如下所示:

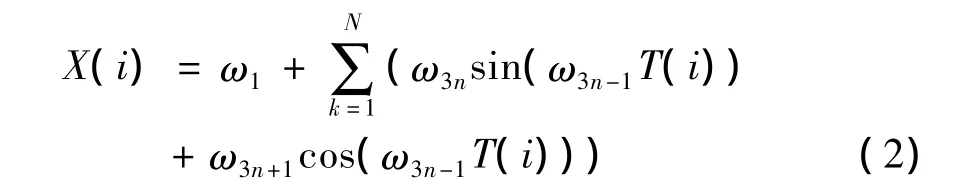
该网络的误差是所有点误差平方和的一半，当误差值小于一定值时可认为该网络收敛.

2 基于RPROP神经网络的谐波分析算法

2.1 RPROP神经网络的算法原理

为了有效提高神经网络的收敛速度，本文采用了RPROP算法来训练多层前馈神经网络.假设Δi(n)为神经网络的可变参数调整量的幅值，其中，n为神经网络迭代的次数.则Δi的表达式如下所示:

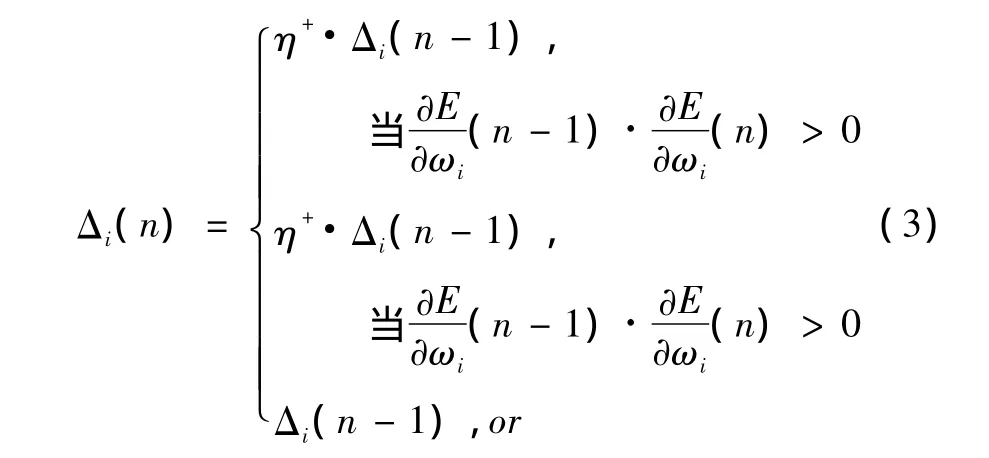
其中:E—神经网络的误差;

W—由神经网络中可变参数组成的矩阵;

wi—矩阵中得第i个元素.

假设可变参数的调整量为Δωi(n)，则其表达式如下所示:

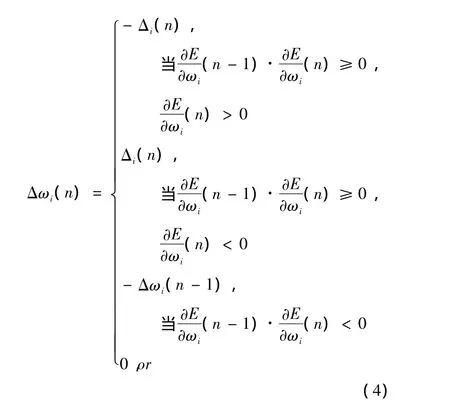
2.2 初始化算法

对RPROP算法而言，如果其初始点选择不合适，可能出现神经网络收敛于局部的极小值，导致不合理情况出现.因此，在非同步采样情况下，引进加Hanning窗插值傅立叶算法来弥补.该算法的计算量较小，并且误差不大.

2.3 RPROP算法计算步骤

本文所提出的基于RPROP神经网络电力系统谐波分析，其计算步骤如下.

(1)根据幅值、相角校正公式来获得神经网络可变参数的初始值;

(2)确定训练目标以及允许的最大迭代次数;

(3)根据公式(3)求解可变参数调整量的幅值;

(4)根据公式(4)求解可变参数的调整量;

(5)根据公式(5)确定可变参数的最优值;

(6)计算误差E.当E小于确定目标或迭代次数大于允许的最大迭代次数时，计算结束，否则，进行步骤(2).

3 仿真模拟分析

对RPROP算法以及FFT-ANN算法进行高精度以及低精度两种情况的仿真分析比较，所采用的信号为:

表1 加Hanning窗插值算法的误差

表2 高精度时FFT-ANN和RPROP两种算法比较

表3 低精度时FFT-ANN和RPROP两种算法比较

从表1可以看出，通过加Hanning窗插值算法的误差明显大于表2及表3中采用神经网络训练后的误差.而从表2可以看出，在高精度目标下，RPROP神经网络算法在经过96次训练后其误差平方和能够满足小于10－8的目标，并且最大误差出现在相位上，仅为 3.53 ×10－4°;而 FFT-ANN 神经网络算法在经过200次训练后起误差平方和远大于为10－8的目标，此时仍没有收敛，并且各分量的误差远远大于RPROP神经网络算法所产生的误差.在高精度目标下，RPROP神经网络算法耗时为58.0 ms，仅为FFT-ANN神经网络算法耗时125.3 ms的一半，并且前者的网络参数无需选择，后者需要对网络参数进行不断试验选择最优值，因此RPROP神经网络算法的适应性要高于FFT-ANN神经网络算法.从表3可以看出，在低精度目标下，RPROP神经网络算法在经过6次训练后其误差平方和能够满足小于0.05的目标，而FFT-ANN神经网络算法在需要经过90次训练达到目标，网络能够收敛，并且，RPROP神经网络算法耗时为3.4 ms，仅为FFT-ANN神经网络算法耗时57.7 ms的1/17，因此RPROP神经网络算法的实时性要高于FFT-ANN神经网络算法.

4 结论

基于RPROP神经网络的电力系统谐波分析能够有效避免意义不大的幅值信息的干扰，该算法由于利用了启发式的训练模式，大大提高了网络的收敛速度.与 FFT-ANN神经网络算法相比，基于RPROP神经网络算法提高了谐波分析的精确度、适应性以及实时性，并且网络参数无需选择，具有一定的参考价值和实用价值.

［1］蒋春芳，刘 敏.基于双插值FFT算法的间谐波分析［J］.电力系统保护与控制，2010，38(3):11 －14，19.

［2］宁薇薇，裴 源，刘立彦，等.基于傅立叶基函数神经网络算法的电力系统间谐波分析方法［J］.电力系统保护与控制，2008，36(12):12－16.

［3］李自成，孙玉坤.一种神经元自适应谐波电流检测方法的数字仿真［J］.电力系统保护与控制，2009，37(5):1 －5，51

［4］柴旭峥，文习山，关根志，等.一种高精度的电力系统谐波分析算法［J］.中国电机工程学报，2003，23(9):67 －70.

［5］向东阳，王公宝，马伟明，等.基于FFT和神经网络的非整数次谐波检测方法［J］.中国电机工程学报，2005，25(9):35 －39.

［6］Riedmiller M，Braun H.A direct adaptiv method for faster back propagation learning:the RPROP algorithm［C］//Proceedings of the IEEE International Conference on Neural Networks.Piscataway(NJ):IEEE ，1993 ，586－591.

［7］谢 明，丁 康.频谱分析的校正方法［J］.振动工程学报，1994，7(2):172 －179.

［8］律方成，徐志钮，李和明.结合粗调和细调的电力系统谐波分析算法［J］.电工技术学报，2007，22(6):114 －120.