关于真分数分拆的一个一般性结论及几个推论

●

(石浦中学 浙江象山 315731)

关于真分数分拆的一个一般性结论及几个推论

●陈剑

(石浦中学 浙江象山 315731)

定理1设n∈Z+，则

证明定理3需要用到下面的引理.

证明设

(4)

(1)若(x,y)=1，因为(x,y)=(x,x+y)=(y,x+y)=1，p为素数，要使式(4)能表成2个不同单位分数之和，则x|pm，y|pm,所以x,y中有一个为1.不妨设x=1，则y=pt(1≤t≤m)，代入式(4)得式(3).

(2)若(x,y)=d(d>1)，令x=x1d,y=y1d代入式(4)约分后归结为(x,y)=1的情况.

综上所述，y有m种取法，引理得证.

定理3的证明由引理得

则

(5)

下面看定理3的几个推论.

下面给出几个应用的例子.

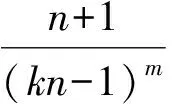
证明我们只需对(kn-1)t+1按n+1泰勒展开，即

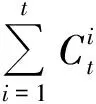
则(n+1)|[(kn-1)t+1]等价于(n+1)|[(-k-1)t+1]，由推论1，2即可得证.

在例1中,取k=3，m=2，n≠16,再由定理1，2即可证得，此处略去.

[3] 周兰林.关于真分数分拆的一个一般性结论[J].中学数学教学参考(上旬),2006(3):57.