一道“希望杯”赛题的拓广及其应用
2011-11-27
●
(漾濞县第一中学 云南大理 672500)
一道“希望杯”赛题的拓广及其应用
●范花妹秦庆雄
(漾濞县第一中学 云南大理 672500)

( )

(2010年第21届“希望杯”全国数学邀请赛高二第一试试题)
这道题设计新颖、综合性极强,集中考查了多个知识点,是一道有较好区分度的好题,值得我们深入研究.若将其推广为一般问题进行研究,则可获得如下命题.



图1
证明如图1,不妨设点A位于点B的上方,直线l是与焦点F相对应的准线,点A,B在l上的射影分别为C,D,点B在AC上的射影为H.由椭圆定义得

即

在Rt△ABH中,有
|AH|=|AC|-|HC|=|AC|-|BD|=

(1)


将式(2)代入式(1),得

(3)
又
|AB|=|AF|+|FB|=λ|BF|+|FB|=
(λ+1)|FB|,
(4)
且λ≠1,由式(3)知|AH|≠0,所以在Rt△ABH中,

将式(3)和式(4)代入式(5),得

即

若将椭圆拓广到双曲线或抛物线中进行研究,则可获得如下命题.



命题2和命题3的证明与命题1类似,此处从略.根据相似性,可将上述3个命题统一为:

上述定理反映了圆锥曲线焦点分弦所得的比和弦所在直线的倾斜角(或斜率)之间的内在联系.如果掌握了上述定理,那么圆锥曲线焦点分弦所得的比和弦所在直线的倾斜角(或斜率)之间的问题便可迎刃而解.下面以近2年的高考题为例,说明上述定理在解题中的应用.
先给出例1的解答.




( )
(2010年全国数学高考理科试题Ⅱ)
解因为

所以由定理得

解得

因此
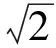
故选B.

(2010年全国数学高考理科试题Ⅰ)
解设椭圆的中心为O,焦点弦BD所在直线的倾斜角为θ.在Rt△BOF中,有

又λ=2,由定理得

解得


(2010年辽宁省数学高考理科试题)


解得


( )

(2009年全国数学高考理科试题Ⅱ)

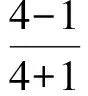
解得

故选A.
从上面几例可以看出,本文给出了圆锥曲线中一个统一的定值,提供的方法可有效地解题,特别是选择题和填空题.需要注意的是,由于该定理不是课本结论,在求解解答题时不宜直接作为解题依据,但可以利用证明定理的思路直接求解.
