一个求解不等式约束优化问题的非内点型可行QP-free算法

陈 玉,陈内萍,段 玉

(湖南商学院信息学院,中国 长沙 410205)

本文考虑求解如下不等式约束优化问题

且假定f:Rn→R,gi:Rn→Rn都是连续可微的.为表述方便，记F={x∈Rn:gi(x)≤0,i∈I}.

对上述问题(P)的求解，目前存在很多方法，如SQP、可行方向法、罚函数法、内点法等，其中QP-free方法是求解上述问题的有效方法之一[2-12].该算法的思想最早见于文献[1],而由Panier,Tits和Herskovits[4]首次提出．在Panier-Tits-Herskovits算法的每一个迭代，仅需求解2个不同的线性方程组和一个线性最小二乘问题．Gao,He和Wu[5]也提出一个求解问题(P)的可行QP-free 算法，不同于Panier,Tits和Herskovits算法，在不要求稳定点数目有限的条件下，他们的算法产生的点列的聚点都是问题(P)的KKT点.但是，在收敛性的证明中，他们必须假定乘子序列有界.Qi基于互补函数和KKT条件，提出了一个求解问题(P)的可行QP-free 算法[8]，他们在无严格互补条件下证明了迭代矩阵的一致非奇异性和近似乘子序列的有界性.Yang, Li和Qi[9]通过引进一个工作集的概念，提出了一个新的求解问题(P) 的可行QP-free 算法,该算法仅考虑工作集内的约束，这使得计算量大大减少；在该算法的每一个迭代，仅需求解4个系数相同的线性方程组.但是，对于上述几种可行QP-free 算法，迭代点必须是F的内点.

本文在文献[9]的基础上提出了一个求解问题(P)的非内点型修正可行QP-free算法，该算法不要求迭代点必须是F的内点；在算法的每一个迭代，只需求解4个系数相同的线性方程组；在合适的条件下，该算法具有全局收敛性和局部一步超线性收敛速度.

1 算法描述

我们首先给出该算法的有关记号，然后给出该算法.为此，我们给出如下假设：

(H1) 集合F是有界的.

(H2) 对任意x∈F，向量组{▽gi(x),i∈I0(x)}是线性无关的，这里I0(x)={i|gi(x)=0}.

性质1[6](i)对每个x∈F，关于λ的二次函数‖▽xL(x,λ)‖2+‖G(x)λ‖2存在唯一的极小者λ(x)=-M-1▽g(x)T▽f(x)，这里

L(x,λ)=f(x)+λTg(x)G(x)=diag(gi(x)),M(x)=▽g(x)T▽g(x)+G(x)2.

(ii)乘子函数λ(x)在F上是连续可微的.

(iii)如果(x*,λ*)∈Rn×Rm是(P)的KKT点对，那么λ(x*)=λ*.

非内点型可行QP-free算法步骤：

参数及有关初始值：β∈(0,1),μ∈(0,0.5),ν>2,τ∈(2,3),ϑ∈(0,1),M0>0,σ∈(0,1),σ1>1,x′∈F，H1是一个对称正定矩阵，ε0>0,k=1.

步骤1. 令ε=εk-1和M=Mk-1.

步骤2. 令Ak(ε)=A(xk,ε)和Vk(ε)=V(xk,Hk;Ak(ε)).如果▽gAk(ε)(xk)非满秩或‖Vk(ε)-1‖>M，那么令ε=σε和M=σM，进入步2.

步骤3. 令εk=ε和Mk=M,Ak=Ak(εk),Vk=V(xk,Hk;Ak).

步骤4. 搜索方向的计算：

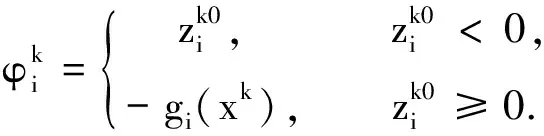
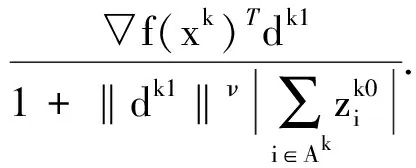
步骤6. 线搜索：

计算序列{1，β，β2，…，}中满足如下不等式组的第1个数tk：

注从H2和Hk的对称正定性易知，V(xk,Hk,Ak)是非奇异的.

从算法中，不难得到如下关系:

(1)

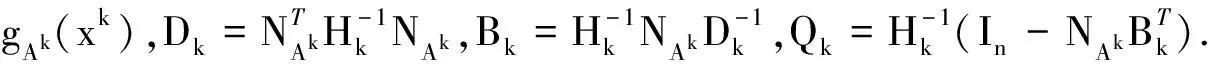
引理1(i)如果dk1=0，那么xk是问题P的KKT点.

(ii)如果dk1≠0,那么▽f(xk)Tdk<0,▽gi(xk)Tdk<0,∀i∈I0(xk).

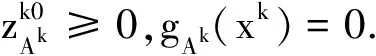
(ii)该结论的证明类似于文献[9]中引理2.2的证明.

2 全局收敛性分析

在本节，我们将分析该算法的全局收敛性.首先假设：

(H3)对所有的k和d∈Rn，存在正常数C1和C2满足C1‖d‖2≤dTHkd≤C2‖d‖2.

引理2[9]序列{(dk0,zk0)},(dk1,zk1),(dk2,zk2)都是有界的.

引理3[9]对所有的k,存在正常数κ满足‖dk-dk1‖≤κ‖dk1‖ν.

引理4假设x*是该算法所生成序列xk的一个聚点，{xk}K0→x*，如果{▽f(xk)Tdk1}K0→0，那么x*是问题P的KKT点且{zk0}K0存在一子列收敛到对应于x*的唯一乘子向量λ*.

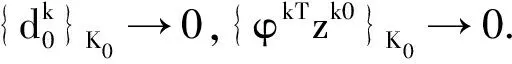
又g(x*)≤0，因此x*是问题P的KKT点.由乘子向量的唯一性知：{zk0}K1收敛到对应于x*.的唯一乘子向量λ*.

类似于文献[9]中的定理3.1的证明，我们可得如下全局收敛性定理.

定理1如果(x*,λ*)是该算法所生成序列(xk,zk0)的一个聚点，那么(x*,λ*)是问题P的KKT点.

3 收敛速度分析

本节我们将分析该算法的收敛速度.假定(x*,λ*)是该算法所生成序列(xk,zk0)的一个聚点，那么从全局收敛性定理知，(x*,λ*)是问题P的KKT点.为讨论方便，我们记I0=I0(x*).为此，我们需做如下假设：

(H4)(i)函数f(x),gi(x)都是二次连续可微的.

(ii)在(x*,λ*)处严格互补条件成立，即λ*-g(x*)>0.

引理5假定(H1),(H3)，(H4)，(H5)成立，则整个序列{xk}收敛到x*，即xk→x*,k→∞.

证从(2.1)和引理2.1可知

f(xk+1)≤f(xk)+μtk▽f(xk)Tdk≤f(xk)-μϑtkdk1THkdk1.

考虑到(H1)和(H3)，可得到tk‖dk1‖→0.因此利用引理3可得，tk‖dk‖→0.

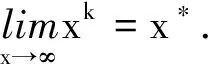
下面的引理见文献[13]中的定理2.3和2.7.

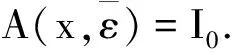
类似于文献[9]中的推论4.1,我们可得如下引理.

引理7假定(H1),(H2),(H3)，(H5)成立，则对充分大的k,有Ak=I0成立.而且有如下关系成立：

(i)dk0→0,dk1→0,dk→0(k→∞)

(ii)zk0→λ*,zk1→λ*,zk→λ*(k→∞)

(iii)如果还有(H4)成立，则对充分大的k，有φk=-gI0(xk).

为得到该算法的超线性收敛性，一个关键性要求是在解的附近单位步长能达到.为此，下面的假设是必要的.

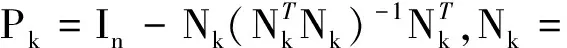
该引理的证明见文献[9]中引理4.3,4.4.

类似于文献[9]中引理3.5的证明，我们可得到如下引理.

引理9假定(H1)～(H5)成立，则当k充分大时，步长tk≡1.

基于上述一系列引理，我们可得如下定理

参考文献：

[1] HERSKOVITS J. A two-stage feasible direction algorithm for nonlinear constrained optimization[J].Math Prog, 1986,36(1):19-38.

[2] PANIER E R, TITS A L. A supperlinearly convergent feasible method for the solution of inequaality constrained optimization problems[J].SIAM Contr Opti, 1987,25(7):934-950.

[3] WIEST E J, POLAK E. A generalized quadratic programming based phase I-phase II method for inequality constrained optimization[J].Appl Math Opti, 1992,26(2):223-252.

[4] PANIER E R, TITS A L, HERSKOVITS J N. A QP-free globally convergent,locally superlinearly convergent algorithm for inequality constrained optimization[J]. SIAM J Contr Opti, 1988,26(5):788-811.

[5] GAO Z Y, HE G P, WU F. Sequential syestems of linear equations with general constrains[J].J Opti Theo Appl, 1997,27(1):24-33.

[6] LUCIDI S. New results on a continuously differentiable penalty function [J]. SIAM J Opti, 1992,2(4):558-574.

[7] Q L Q, YANG Y F. Globaally and supearliearly QP-free algorithm for nonlinear constrained optimization[J].J Opti Theo Appl, 2002,113(2):297-323.

[8] QI H D, QI Q L. Anew QP-free,globallyconvergent, locally superlinearly convergent algorithm for inequality constrained optimization[J].SIAM J Opti, 2000,11(2):113-132.

[9] YANG Y F, LI D H, QI L. A feasible sequential linear equation method for inequality constrained optimization [J].SIAM J Opti, 2002,13(6):1222-1224.

[10] FACCHINEI F, LAZZARI C. Local feasible QP-free algorithms for the constrained minimization of SC1 functions[J]. J Opti Theo Appl, 2003,119(3):281-316.

[11] FACCHINEI F, LUCIDI S. Quadratically and superlinearly convergent algorithms for the solution of inequality constrained minimization problems[J].J Opti Theo Appl, 1995,85(3):256-289.

[12] ZHU ZH B. An interior point type QP-free algorithms with superlinearly convergent for inequality constrained. optimization[J].Appl Math Mod, 2007,31(6):1201-1212.

[13] FACCHINEI F, FISCHER A, KANZOW C. On the accurate identification of active constraints[J]. SIAM J Opti, 1999,9(1):14-32.