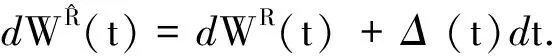债券价格随机时重设型熊市认售权证的定价

欧 辉 李代绪，杨向群

(1.湖南师范大学数学与计算机科学学院，中国 长沙 410081；2.长沙商贸旅游职业技术学院，中国 长沙 410004)

重设型熊市认售权证作为单点重置期权的一个应用，由Gray及Whaley[1-2]介绍，由国际财务公司于1996年创新发行，并在纽约股票交易市场及芝加哥期权交易市场两地交易．它以S&P500指数作为标的资产，但它可于发行后3个月重设履约价．也就是说，从原发行日后满3个月的交易日，若当天S&P500指数的收盘价格高于原履约价，则该权证的履约价重设为当日指数的收盘价格．这与一般不可重设履约价的指数认售权证不同，因含有重设履约价的特征，重设型熊市认售权证的价值高于一般的指数认售权证．重设型熊市认售权证可应用于组合避险，保护投资组合(或共同基金)的价值不因股价下跌遭受损失．但若股价指数不跌反而上升时保险的面额可随着指数价位上升而重设为当时指数价位所代表的价值．这种重设特征提供投资组合更有价值的保护，是一般认售权证所不及之处，因此吸引了很多投资者的兴趣．文献[3]中推导了当无风险利率、股票指数的连续红利率及瞬时波动率都是常数时重设型熊市认售权证的定价公式，但是其中的计算过程有很多处错误，导致最后结果也是错误的．本文推导了当无风险资产—零息票债券的价格过程满足一个由布朗运动驱动的随机微分方程时，重设型熊市认售权证的定价公式．

1 模型介绍

重设型熊市认售权证实际上是一种特殊的欧式重置卖权.本文中规定：期权到期日为T(T>0)，标的资产为股票指数，其价格过程为S(t)(0 ≤t≤T)，原履约价为K，事先指定的可重设履约价的时点为τ，即在τ时刻，期权持有者可以将原履约价K重设为S(τ)，当然也可以选择不重设．

设t时刻股票指数价格S(t)(0 ≤t≤T)满足随机微分方程：

dS(t)=[μ(t)-q(t)]S(t)dt+σ(t)S(t)dW1(t).

市场上存在一种无风险资产：零息票债券．t时刻其价格B(t)(0 ≤t≤T)满足随机微分方程：

dB(t)=r(t)B(t)dt+δ(t)B(t)dW2(t),

其中μ(t)，q(t)，σ(t)分别是股票指数的期望收益率，连续红利率和瞬间波动率，r(t)，δ(t)分别为债券的期望收益率和瞬时波动率，它们都是时间t的确定性函数，B(T)=1．

{Wi(t)，0 ≤t≤T}(i=1,2)是定义在概率空间(Ω，F，P)上的两个一维标准布朗运动，P为市场概率测度，dW1(t)dW2(t)=ρdt，ρ为正常数．

重设型熊市认售权证的到期价值CT可以用公式表示如下：

其中α为任意常数．

2 风险中性概率测度的转换

dS*(t)=μ(t)S*(t)dt+σ(t)S*(t)dW1(t).

定义测度Q如下：

且令

则在Q测度下Z(t)满足

令

则WQ(t)为Q下的标准布朗运动，且

令

定义测度R满足

令

dWR(t)=dWQ(t)-θ(t)dt,

则WR(t)为等价鞅测度R下的标准布朗运动，且在R下

3 模型定价

定理1债券的价格过程受布朗运动驱动时，重设型熊市认售权证在t时刻(t<τ)的价格C(t)为：

其中N(x)为一维标准正态分布累积分布函数，N(x,y,ρ)为二维标准正态分布累积分布函数．

证根据风险中性定价原则，期权在t时刻(t<τ)的价格为：

C(t)=B(t)ER[CT|Ft]=

利用测度的转换和鞅的性质，第一部分C1计算如下：

C1=αB(t)ER[I{S(τ)>K,S(T)K,S(T)

αB(t)PR{S(τ)>K|Ft}PR{S(T)

其中第3个等式利用了布朗运动的独立增量性．

且

在R测度下用类似的方法求C3：

C3=αB(t)ER[I{S(τ)≤K,S(T)

所以当债券的价格过程受布朗运动驱动时，重设型熊市认售权证在t时刻(t<τ)的价格C(t)为：

证毕．

定理2当债券的价格过程受布朗运动驱动时，重设型熊市认售权证在t时刻(t≥τ)的价格C(t)为：

其中

证当t≥τ时，S(τ)已知，所以期权履约价是否被重设也已知．因为期权为卖权，若S(τ)≤K，则履约价不被重设，因此

若S(τ)>K，则期权履约价被重设为S(τ)，因此

证毕．

鉴于篇幅，文中将很多具体的运算过程都省略了.文中用到的鞅方法定价，是一种很巧妙的方法，现在也很流行，这种方法比起解随机偏微分方程要简单多了，而且对于奇异期权的定价也能得出一个显示表达式．同样的方法我们也可以求出在零息票债券价格过程服从由布朗运动驱动的随机微分方程的情形下，重设型牛市认购权证的定价公式(只不过重设型牛市认购权证是看涨期权，到期价值的表达形式有点不同，但计算方法和技巧都是一样的，有兴趣的读者可以计算一下，鉴于篇幅，这里不再阐述)．

参考文献：

[1] GRAY S F, WHALEY R E. Valuing bear market reset warrants with a periodic rest[J]. J Derivatives, 1997, 5(1): 99-106.

[2] GRAY S F, WHALEY R E. Reset put options: valuation, risk characteristics and an application[J]. Australian J Management, 1999, 24(1): 1-20.

[3] 陈松男. 金融工程学[M]. 上海: 复旦大学出版社, 2002.

[4] DAI M, YUE-KUEN KWOK. Options with combined reset rights on strike and maturity[J]. J Economic Dynamics Control, 2005，29(9)：1495-1515.

[5] 姜礼尚. 期权定价的数学模型和方法[M]. 北京: 高等教育出版社, 2003.

[6] 薛 红, 彭玉成. 鞅在未定权益定价中的应用[J]. 工程数学学报, 2000(3):135-138.

[7] 严加安. 鞅与随机积分引论[M]. 上海：上海科技出版社, 1981.

[8] 欧 辉,姚落根,杨向群.重置期权的一种创新及其定价[J]. 湖南文理学院学报：自然科学版,2009,21(3):13-16.

[9] 欧 辉,莫晓云,贺 磊.债券受布朗运动驱动时幂型支付重置期权的定价[J]. 经济数学,2009，26(4):20-25.

[10] OU H. Pricing the innovative reset options with power payoff：proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM), October 22-24, 2010, Shanxi,Taiyuan, 2010[C]. Taiyuan:[s.n.],2010.