基于动力学性能优化的叉车减震垫检测机构设计

刘传让 ，石怀荣, ，胡 娟

(1.蚌埠市行星工程机械有限公司，安徽 蚌埠 233010；2.蚌埠学院 机械与电子工程系，安徽 蚌埠 233000)

减震垫性能检测的机械装置运动速度高、构件多、运动复杂，是一个典型的多激励、多响应的动态系统，它在高速运动时会产生较大的惯性力，对机架和其他部件形成激励，导致强烈的振动与噪声，影响了机构本身的稳定性，并会降低减震垫性能检测的精度.虽然多杆机构在许多机械中被广泛采用，但是不同的使用性能与要求使得其构件的结构组成完全不同，所以在设计时不能照搬照抄.而且，用两套机构组合而成的机构杆件多、运动关系复杂、涉及的参数较多，仅凭经验不能设计出最优的机构.本文从机构功能与性能优化设计的角度出发，基于降低机构振动的目的，对机构进行了动力学分析.试验表明，基于动力学性能优化设计的机构对降低振动、改善其动态稳定性能有良好的效果.

1 减震垫性能检测装置的运动分析

图1 减震垫性能检测的机构运动简图Fig.1 Simple statement of mechanism kinematics of performance tests for shock pad

减震垫性能检测机械装置的主体部分是由做旋转运动的曲柄通过连杆驱动摆杆摆动，由此驱动压杆带动滑块做往复直线运动.滑块开始工作做直线运动，按预定的检测要求对减震垫施加压力，图1为减震垫性能检测机构的运动简图.由于惯性力表达式较复杂，分析推导过程很容易出错，特别是在进行多杆机构惯性力的计算时，公式太繁杂．本文通过对机构运动进行分析，采用复数矢量法建立起机构惯性力的参数方程.相对于直角坐标法，矢量法既节省计算量，又有规律可循，不易出错.

如图1所示，取机构铰接点O为坐标原点，各构件质心的运动方程可表示为下式的形式：

(1)

其中：Ri为矢量表示的各构件以O为坐标原点的质心运动方程；

ri为各构件以一运动副为端点的构件质心运动方程；

Li为各构件的矢量表示；

φi为各构件的矢量表示Li与x轴正向的夹角.

2 机构中各构件的惯性力分析

由理论力学可知，质点的惯性力定义为质点质量与其加速度之积，所以各构件的惯性力为

(2)

其中，mi(i= 1，2，…7)为各构件的质量.

应用复数矢量建立起构件运动相关的关系式，图1所示的机构中L1、L2、L3和L4组成的四连杆机构构成一个封闭矢量环，因此有：

L2=L1-L4-L3,

(3)

l2ejφ2=l1ejφ1-l4ejφ4-l3ej(π-φ3-θ3).

(4)

对式(4)取虚部得到连杆l2的转角φ2为

(5)

对式(5)等号两端各自进行点积运算，整理后得

(l2)2=(l1)2+(l4)2+(l3)2+2l1l4cos(π+θ4+φ1)-2l3l4cos(π+θ4+φ3)-2l1l3cos(φ1-φ3).

(6)

由此得出:asinφ3+bcosφ3+c=0,其中,a=-2l1(l3sinφ3+l4sinφ4),b=-2l1(l3cosφ3+l4cosφ4),c=(l1)2+(l3)2+(l4)2-(l2)2+2l3l4cos(φ3-φ4).

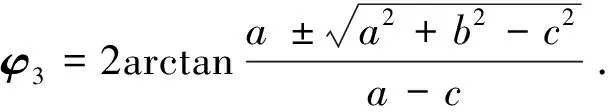
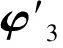
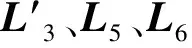
(7)

(8)

由此,机构的惯性力可以表示为各构件转角φ1的函数，而且当主动件1以角速度ω匀速转动时,机构的惯性力即可为时间t的函数：

Fi=mif″(φi),

(9)

经简化整理后,

(10)

3 基于减振目标优化的机构设计模型

叉车减震垫作为叉车中降低振动的一个主要构件，在机械的减振中起到了重要的作用，产品性能要求其在每秒3 000～4 500次受力、零位移点在1.5 mm时，动态刚度小于等于320 N/mm.减震垫性能检测的机械装置采用曲柄摇杆机构和曲柄滑块机构组合而成的多杆机构，曲柄摇杆机构和曲柄滑块机构是许多机械中常用的传递运动和动力的机构形式,其中，滑块机构用来传递检测减震垫所需要的力，而摇杆机构则用来加强整个机构在工作时的稳定性[2].要对机构进行优化设计、减少其对机体的激励，首先应确定合理的目标函数与设计变量.

3.1 目标函数

机体的振动是机构惯性力作用的结果，机构要优化，降低激振力就成为首要问题，激振力的最大值和均方根值都是可选取的优化目标.但是,机构的惯性力是随时间变化的，表征其能量大小更有意义的指标是它们在一定时段内的均方根值,由以上分析得出减震垫性能检测机械装置激振力的均方根值,其数学表达式为

(11)

由此，降低激振力作为目标函数，如式(12)所示：

(12)

3.2 设计约束

减震垫性能检测装置优化设计的约束条件包括边界约束和性能约束，边界约束主要是设计变量的边界取值范围约束，性能约束主要包括保证机构工作的准确性，同时要求满足机构运动的协调性、几何的合理性、机构结构的布置、传动角的限制、避免可能存在的运动干涉及“死点”位置等.由于非独立参数的计算会使机构中的曲柄机构自动成立，由此，约束条件不需考虑曲柄机构成立的条件，可建立如下的约束条件,如式(13)所示:

(13)

3.3 设计变量

有些性能工作参数实际上是设计目标，由于这里所进行的设计是以不改变机构的结构形式和运动规律为前提的，综合考虑影响送检机构性能的各种关键因素，故理论上所有构件的构件长度li质量mi和质心位置ri、θi都可作为设计变量.但是,从实际的机构制造和装配角度出发，并考虑到构件的具体形状和工艺实现的可能性，最终确定的设计变量为

X=[x1,x2,x3,x4,x5]=[l1,l5,r5,r5,β].

(14)

4 算例分析与模拟验证

原始参数可根据经验或类比的方法获得，其中曲柄转速n=24×103r/min,这是检测机构工作时常用的转速，也是评价其动态性能的标准转速.由于经验不同，选取的优化初始数据就不同，为了验证优化结果，在初始值数据的基础上，随机产生10%范围以内波动的4组数据.分别对5组数据进行Mathcad优化，然后将后4组优化结果与第1组进行比较，以验证优化的鲁棒性.

利用VB中的RND函数产生在0.95～1.05范围内的随机值，分别乘以初始计算的参数,然后进行整型处理,可以得到5组不同的初始参数作为优化的初始值.设计变量的初始值及上下限及优化后的最优值见表1.

表1 设计变量初始值、约束域及优化结果Tab.1 Initial value of design variable,constrained domain and optimize result

由表1中的参数可以看出,最大优化的波动范围在1.37%以内，而其他数据范围均在0.97%以内.这表明,减震垫检测装置优化设计模型的建立与 Mathcad所采用的内部优化方法的优化结果具有鲁棒性.课题组为验证检测机构设计模型的可靠性，与蚌埠某叉车配件生产厂家合作，根据该叉车配件厂家和用户的要求，采用优化计算结果的第3组(l1=186 mm，l5=238.7 mm，r5=4.5 mm，r5=24 mm，β=176°)对检测机构进行了设计,使其质量和形状参数在满足强度等要求的前提下尽可能地接近计算所得的最优变量.对设计后的检测机构进行了功能试验，对不同的转速下机体多点x向的振动进行了测试，由测试数据可以看出，采用优化设计后，机体多点的振动响应在不同转速下均显著降低.其中，在24×103r/min的评价转速下，机体多点的位移响应峰值为216 μm, 低于预期值，减振效果较为明显.

5 结论

本文着眼于降低机构激振力的动态特性，以其惯性力的均方根作为目标函数，通过机构的优化设计来减少其对机座的激励，是一种从振源上解决问题的主动方法.机构与结构优化设计是现代机械设计发展的需要,即建立有针对性的优化目标函数和约束条件，根据工作性能的特定要求或已有构件的尺寸进行优化，直至获得满意的设计方案.基于机构工作性能的要求和工件检测的运动学特性，提出了机构的设计研究模型，建立了检测机构的优化设计模型并进行了具体的算例分析，为自主研制新型、高效、节能的减震垫检测装置奠定了理论基础.减震垫检测装置的优化试验模型应用于生产厂家，取得了良好效果，验证了模型的正确性与可靠性.

参考文献：

[1] 朱成实，吴琼，吴敬东. 用Mathcad对注射机增力机构进行优化设计[J]. 机械设计，2002, 22(1)：56-58.

[2] 刘善林，张勇.连杆机构运动特性的解析算法及仿真研究[J]. 机械研究与应用，2007,22(6)：37-39.

[3] 余跃庆，李哲. 现代机械动力学[M].北京：北京工业大学出版社，1998.

[4] 孙恒，陈作模. 机械原理[M].北京：高等教育出版社, 2007.

[5] 濮良贵. 机械设计[M]. 北京：高等教育出版社, 2007.

[6] 孙靖民. 机械优化设计[M]. 北京：机械工业出版社,2005.