扩散过程的元胞自动机模拟

李延升，侯珂珂，张保林

(1.许昌学院 化学化工学院，河南 许昌 461000； 2.郑州大学 化工与能源学院，河南 郑州 450007)

扩散过程是重要的质量传递方式之一，元胞自动机则是近年来新兴的仿真模拟方法.但是，将两者结合，即用元胞自动机研究扩散过程的文献却相对较少.有关此类的报道，多是和反应过程相关联且研究的侧重点放在后者[1]，很少见到用元胞自动机专门研究扩散过程的报道.另外，在有关的报道中，元胞自动机模型的参数往往过多且相互之间的关系复杂，分析时需要综合多门学科的理论，这限制了它的实际应用.作为一种新兴的研究手段，元胞自动机的意图是以极其简单的规则解释或模拟复杂的现象，而有关的报道多数违背了这一意图，无法体现元胞自动机的优越性.本文即从此方面入手，将元胞自动机方法与数学分析方法相对比，给出了生动形象的扩散过程动态画面，为进一步的研究奠定了基础.

1 元胞自动机简介

元胞自动机有时也被称为细胞自动机、点格自动机、分子自动机或单元自动机，它是现代计算机之父Neumann及其追随者提出的想法.20世纪末21世纪初，Stephen将这种带有强烈的纯游戏色彩的原始想法从学术上加以分类整理，最终使之上升到了科学方法论[2].

元胞自动机是一时间和空间都离散的动力系统，散布在规则格网(Lattice Grid)中的每一元胞(Cell)取有限的离散状态，遵循同样的演化规则，依据确定的局部规则同步更新，大量元胞通过简单的相互作用而构成动态系统的演化.不同于一般的动力学模型，元胞自动机不是由严格定义的物理方程或函数确定，而是由一系列模型构造的规则构成，凡是满足这些规则的模型都可以算作元胞自动机模型.因此，元胞自动机是一类模型的总称，或者说是一个方法框架[1-2].元胞自动机最基本的组成为元胞、元胞空间、邻居及规则这4部分.简单来讲，元胞自动机可以视为由一个元胞空间和定义于该空间的变换函数所组成[1-3].

2 扩散过程元胞自动机模型的提出

同普通的元胞自动机一样，本文的元胞自动机也是采用等间隔的点作为元胞.不失一般性，以二维的圆形区域为离散域，以处于中心的某个元胞为圆心，取适当长度的半径，在圆域内的元胞即为该元胞自动机的元胞，正好在圆上的交叉点也看作圆域内的元胞，见图1.以纵横方向上均匀分布的点为元胞，圆域内外的元胞区分非常明确.为了让画面清晰，该图的元胞较少，在实际应用时，元胞数量要比该图多得多.

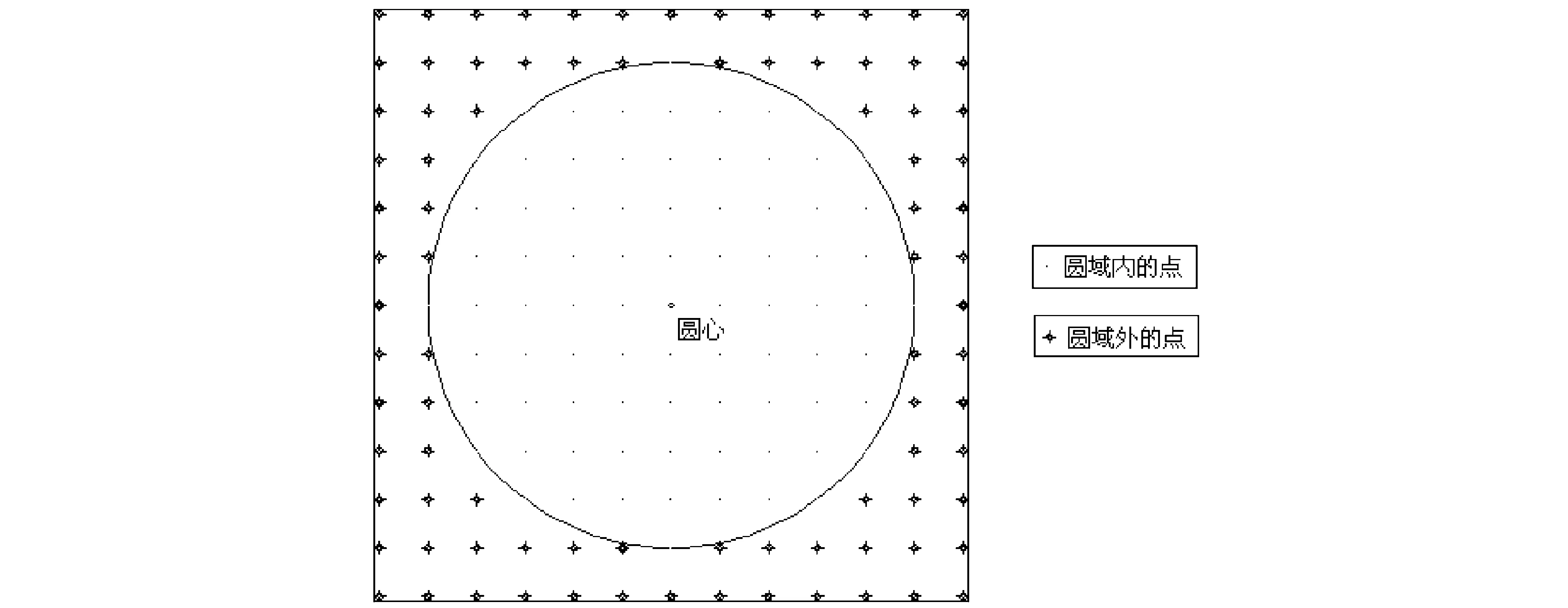
图1 模拟扩散过程的元胞自动机离散域及元胞Fig.1 The discrete region and cells of cellular automata used for simulate the diffusion process

现以元胞自动机分析某一典型的扩散过程.该扩散过程的假设是：(1)参与扩散的物质为A和溶剂M.(2)扩散过程在某一圆形区域及其外界进行.(3)初始时刻，物质A以溶液的形式，均匀地分布在该圆形区域内.随后，A即开始由内到外扩散.显然，在圆形区域中，越靠近圆心的位置，A的浓度越大.(4)圆形区域内同时还有物质B，该物质不参与扩散过程，其浓度均一且不发生变化.(5)圆域外的区域视为无穷大.根据这一假设，如果设该圆形区域的半径为a，某一元胞所在的位置处半径为r，那么在r≥a处，A的浓度为0.

根据扩散过程的特点，元胞的设定及演化规则是：

(1)以元胞0、1、2分别代表物质M、A、B，再用k代表演化次数.显然,k和时间t对应，也是变量.

(2)用元胞1的随机行走代表物质A的扩散.具体规定是：第k次演化时，某元胞1的上、下、前、后、左上、左下、右上、右下的8个邻居中，若有n个为元胞0(n≥1)，则在第k+1次演化时，该元胞1与这n个元胞0的任意一个交换位置.若该交换完毕后，元胞1的位置已经在圆域的边界处，则该元胞1演化为元胞0.

(3)元胞2不发生演化.

(4)根据前文的假设(5)，圆域外界只有元胞0，无元胞1和元胞2.

3 结果及讨论

3．1 演化结果

用一个实例分析.设初始时刻，元胞自动机中，元胞0、1、2所占的量分别为40%、20%、40%，且均匀分布，元胞自动机的离散域是直径为100的圆，用Matlab 编写程序得到的演化图见图2，该图可模拟扩散过程且较为生动形象.

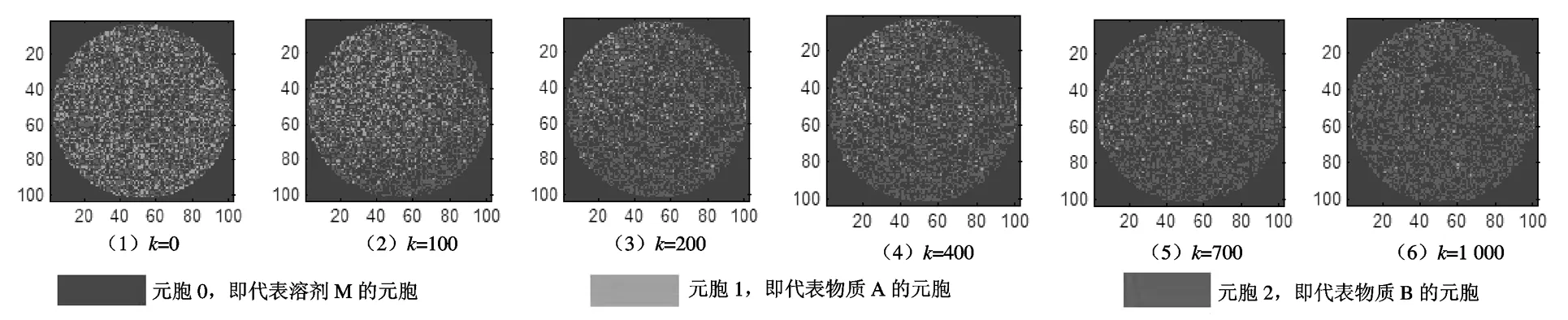
图2 模拟扩散过程的元胞自动机演化示意图Fig.2 Sketch maps simulating the diffusion process with cellular automata

定义：(1)演化次数为k时，圆域内已经扩散到外界的元胞1的数量占初始时刻元胞1的数量的比例为累计扩散率.(2)累积演化的元胞1的数量占初始时刻数量的99%时，对应的演化次数k为ke，ke即为扩散的终点.元胞1的累计扩散率曲线ke/t-k见图3.从图2与图3可以看出，随着k的增大，累计扩散率曲线由陡变缓，说明扩散速率由大逐渐变小.

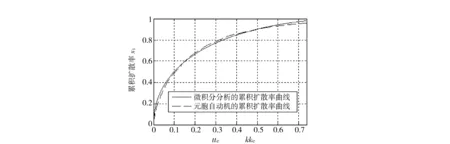
图3 元胞自动机模拟的累积扩散量曲线以及用微积分求得的累积扩散量率曲线Fig.3 The accumulate diffuse amount curves obtained with cellular automata and the calculous respectively

改变元胞自动机的参数，如元胞的数量、比例等，运行程序，得到的累计扩散率曲线基本不变，说明该曲线只受演化规则的影响，与元胞自动机的参数无关.

3.2 微积分分析

再用微积分的方法分析这一扩散过程，并与元胞自动机方法对比.该扩散过程实际上是球形扩散体系在球的大圆截面上的扩散过程.为了更符合实际情况，以球坐标分析.取球心为坐标原点，建立球坐标.设球体内，物质A的浓度为cA，则cA是空间半径变量r和时间变量t的函数，角度方向上无扩散分量.物质A的传递方程为

(1)

初始条件：cA=c0,

(2)

边界条件：cA(l,t) =0,

(3)

以上三式中，cA与元胞1的数量对应；r与元胞自动机某处的位置对应；t为时间变量，与演化次数k对应；DAB为物质A在物质B中的扩散系数，与元胞1的随机行走的情况对应.这三式组成的偏微分方程的解为

(4)

由此，可求得物质A的扩散速率NA(t)和累计扩散率x1：

(5)

(6)

为了进一步阐述的需要，兹列举一个实例，该实例来自文献[6],实例为球形的晕海宁胶囊的扩散控制的释放系统，其药物扩散体系符合本文的假设.胶囊的直径为3.26 mm，晕海宁在控释凝胶层中的扩散系数DAB为3.0×10-7m2/s，由此得

(6a)

用Matlab辅助计算，取n=1 000，即

(6b)

则截断误差r1 000的范围为

截断误差已经足够小，得到的累积扩散率曲线x1/te-t亦示于图3中，便于对比.图中，te为累积释放率达到99%时的t值，与元胞自动机的ke对应.从图3可以看出，两条曲线非常接近.实际上，任意取一DAB的值，并作x1/te-t曲线，结果都是如此，从而说明用元胞自动机的研究结论与用微积分研究的结论是一致的.

4 结 论

以元胞自动机作为方法和手段，通过编写Matlab程序，可以形象、逼真地模拟扩散过程.元胞自动机的核心是，各参数与扩散现象紧密相关，用元胞的演化模拟扩散的过程.元胞自动机模拟的结果与微积分的结论一致，并由实例为佐证.

用元胞自动机模拟扩散过程，虽然具有规则简单、模拟效果较直观等优点，但是所用元胞自动机的演化规则和重要参数，基本上是根据释放的过程而作的人为规定，可以说没有完全脱离经验模型的框架和模式.当然，目前绝大多数元胞自动机模拟的情况也都是这样，这也是元胞自动机尚未被广泛应用的重要原因之一.如何通过理论分析得到演化规则和演化参数，使该模拟过程上升到较高的理论层次，属于进一步研究的内容.

参考文献：

[1] Bastien Chopard, Meichel Droz.物理系统的元胞自动机模拟[M].祝玉学，赵学龙，译.北京：清华大学出版社，2003：1-47.

[2] Stephen Wolfram.A new kind of science[M].Wolfram media, 2002:1-50.

[3] 曹伟.元胞自动机与计算机模拟[J].丹东纺专学报，2005，12(2)：1-4.

[4] Crank J.The mathematics of diffusion[M].Oxford: Oxford university press, 1975:89-103.

[5] 李延升，张保林，张雪梅，等.膜控型缓控释肥料养分释放模型的研究[J].江苏农业学报，2009，25(5)：1033-1038.

[6] Welty J R, Wicks C E, Wilson R E.动量、热量和质量传递原理[M].马紫峰，吴卫生，译.北京：化学工业出版社，2005：338-341.