一个非线性四阶梁方程三解定理的新证明
2011-11-23徐自立焦慧平石宝峰
徐自立,焦慧平,石宝峰
( 1.中州大学 信息工程学院,河南 郑州450044 2.大连理工大学 管理与经济学院,辽宁 大连 116024)
由于四阶梁方程
(1)
描述了一个弹性梁的形变过程,并且在理论和实际中还有许多其他的应用,所以最近BVP(1)的研究备受大家的关注,也取得了一系列的研究成果[1-2].本文将对其中的三解存在性给出一个新的证明.
1 预备知识
定义1 设E是一个实Banach空间,D是E中的开集,泛函J:D→R1在D上Fréchet可微.如果J′(u0)=θ,u0∈D,那么称u0是泛函J的一个临界点,并称c=J(u0)是J的一个临界值.
定义2 设E是一个实Banach空间,J:E→R1是C1泛函.如果{un}⊂E,J(un)有界,J′(un)→θ蕴涵{un}有收敛子列,则称泛函J满足Palais-Smale条件,简称P.S条件.
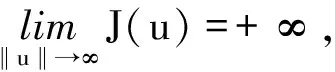
引理2[4]假设J∈C2(H,R1)并且有下界,满足P.S.条件且有一个非退化、非极小、具有有限Morse指数的临界点,那么J至少有3个不同的临界点.
2 主要结论及其证明
定理1 假设下面条件成立:
(H1)f(t,0)=0,∀t∈[0,1];
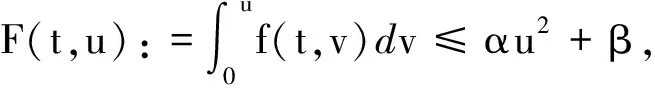
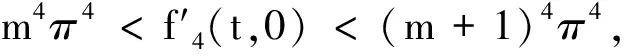
那么BVP(1)在C4[0,1]中至少有3个不同的解.
证明记H=L2[0,1],在H上定义泛函
(2)
由文献[5]易见泛函(2)是问题(1)的能量泛函.下面我们仅需证明J至少有3个不同的临界点.
2.1 证明J∈C2(H,R1)
由(2)可知
J′(u)=u-KfKu,
(3)
J″(u)=I-Kf′(Ku)K,
(4)
所以J∈C2(H,R1).
2.2 证明J在H上有下界
由(H2)知,对任意的u∈H,
(5)
因此,J在H上有下界.
2.3 证明J在H上满足P.S.条件
假设{un}⊂H且∃M1>0使得|J(un)|≤M1及J′(un)=un-KfKun→θ,n→∞.下面证明{un}有收敛子列.
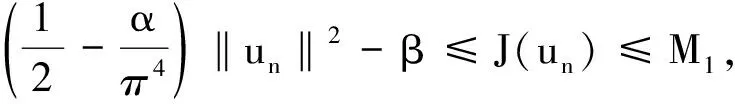
记A=KfK,知A是紧算子,则{Aun}列紧,故存在{Aun}的子例Aun→u0,从而由J′u(n)=un-KfKun→θ知unk-Aunk→θ,所以unh=(unk-Aunk)+Aunk→u0,由此即知{un}有收敛子列.
2.4 证明θ为J的一个临界点
由J′(u)=u-KfKu及f(t,0)=0,∀t∈[0,1]知J′(θ)=θ,即θ为J的一个临界点.
2.5 证明θ为J的一个非退化临界点
为此,即证J″(θ)存在有界逆.
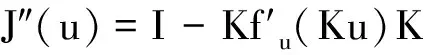
λ=1∈(Cρ(T))=σ(T))=σp(T)∪σc(T)∪σr(T),
而T是紧算子,所以σ(T){0}=σp(T){0},所以λ=1∈σp(T),即λ=1是T的特征值.
设λ为T的任意一个特征值,对应的特征值向量为u≠θ.那么(Tu,u)=(λu,u)=λ(u,u).而
所以T的特征值全部大于0.因为

同理,
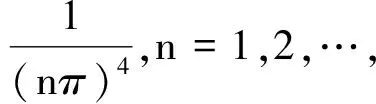
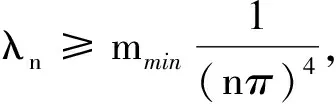
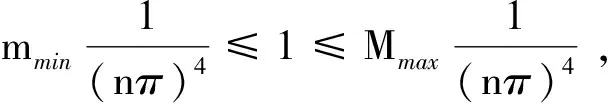
m4π4
由于m,n均为正整数,这显然是矛盾的,所以J″(θ)存在有界逆.
2.6 证明θ为J的一个非极小临界点
由(H3)易知存在ε>0使得
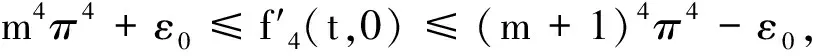
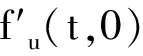
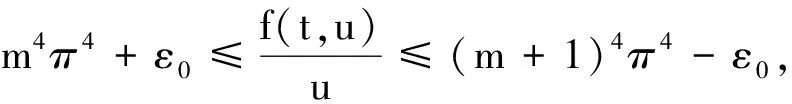
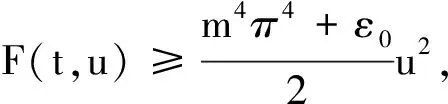
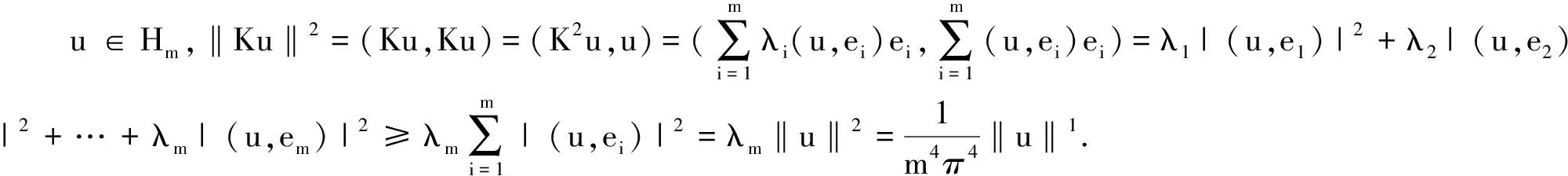
所以,对∀ε>0,取u∈Hm,0<‖u‖<ε,‖Ku‖c≤δ,则
即θ为J的一个非极小的临界点.
2.7 证明θ为J的一个具有有限Morse指数的临界点
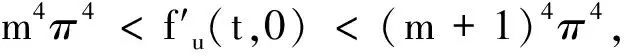
(J′(u),u)=‖u‖2-(f(Ku),Ku)≥‖u‖2-(f(Ku),Ku)≥‖u‖2-|(f(Ku),Ku)|≥‖u‖2-‖f(Ku)‖‖Ku‖>‖u‖2-π4‖Ku‖2≥‖u‖2-π4‖K‖2‖u‖2=0.
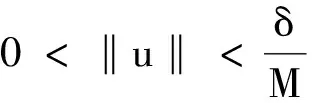
由Morse指数的定义,J在孤立临界点θ处的Morse指数即为H上使得二次型(J″(θ)v,v)负定的极大子空间的维数,记为dimH-.
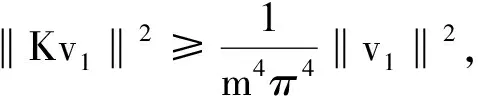
而对于v2⊂Hm⊥,因为
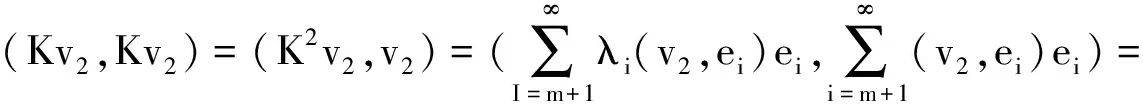
λm+1|(v2,em+1)|2+λm+2|(v2,em+2)|2+……≤
所以
从而dimJ-=m,所以θ点的Morse指数有限.
综合证明2.1~2.7,知J满足引理2的全部假设条件,所以由引理2可知J至少有3个不同的临界点,证毕.
参考文献:
[1] Bai Z, Wang H. On positive solutions of some nonlinear fourth-order beam equations[J].J Math Anal Appl, 2002(270):357-368.
[2] Li F, Zhang Q,Liang Z. Existence and multiplicity of solutions of a kind of fourth-order boundary value problem[J].Nonlinear Analysis, 2005(62): 803-816.
[3] 郭大钧.非线性泛函分析[M].2版.济南:山东科学技术出版社,2001.
[4] 张恭庆.临界点理论及其应用[M].上海:上海科学技术出版社,1986.
[5] 张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版社,1987.
