具有先验信息的地面三维激光扫描地形测量数据去噪算法＊

具有先验信息的地面三维激光扫描地形测量数据去噪算法＊

为防止三维激光扫描数据中的噪声对实景重构造成扭曲,基于消噪的相关理论,提出了 3种具有先验信息的去噪算法,利用高程注记点所提供的先验信息作为去噪依据,分别对比高程插值、最小二乘拟合平面及趋势面,选取适当阈值消去噪声。利用 Ti mble GX200地面三维激光扫描系统获取的地形测量数据进行实验分析,结果表明：高程注记点可以作为先验信息为点云去噪提供依据,并确保去噪后基本符合实体特征。

激光扫描;噪声;先验信息;高程插值;拟合平面

1 引言

三维激光扫描技术作为获取空间信息的有效手段,被广泛应用于工程测量、地形测量、工业制造、矿区变形沉陷监测、历史古迹的调查与恢复等各个领域。在地形测量中,除发展较成熟的机载L I DAR对地观测技术外,地面三维激光扫描系统也被越来越多的应用于地形精细测量[1]。利用三维激光扫描技术获取大量地形扫描数据之后,一个重要的步骤是剔除数据中的噪声点。目前,已有很多关于激光扫描点云去噪算法[2-6]。但现有的去噪算法大都基于相邻点之间的高程突变,认为临近激光脚点间的局部不连续一般不是由地形的起伏所造成,从而突变点被列为非地表点。两邻近点间距离越近,两点高差越大,较高点位于地形表面的可能性就越小[7],这样往往会造成去噪后的扫描数据与实际地形不符,一些存在地形突变的地表点被去除。鉴于此,如果能预先获取测区部分地表点作为先验信息,消除扫描数据中与地形明显不符的噪声点,可以使得建立的三维地形模型更加准确地反映地表变化特征。

2 三种基于先验信息的去噪算法

2.1 基于高程注记点内插高程值的去噪算法

算法利用高程注记点能够大体上反映地表变化趋势这一特征,利用现有地形图逐一内插出点云内每个点的高程值,按照适当阈值剔除点云中实测值与内插值相差较大的点,以达到去噪的目的。由于现有高程注记点数据量较大,故以动态步长搜索待插点周围的点,以高程注记点的平均密度出发,当搜索范围内点数过少时,扩大该点的搜索半径;当点数过多时,缩小搜索半径,最终达到适宜的点数(一般4～10个)。初始搜索步长 R的计算公式为

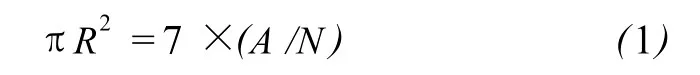
式中A为研究区域面积,N为研究区域内高程点个数。由于研究区域地势平坦,内插方法选择距离加权平均法。在计算待定点 P的内插高程时,使用加权平均值公式：

其中,Z′为待定点 P的内插高程;Zi为第 i个注记点的高程值;n为参考点的个数;pi是第 i个参考点的权重,选用距离平方的倒数为权重,即

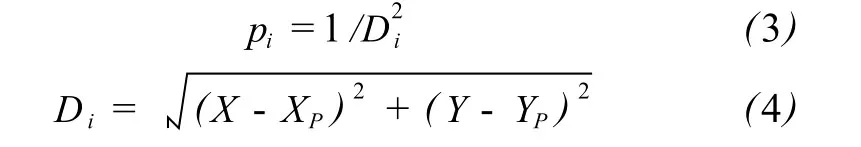
最后,将 P点的内插高程 Z′与实际扫描出的点云高程 Z比较,如果超过所设定的阈值则从点云中去除该点,否则保留。在本算法中,将注记点的高程中误差设为阈值。高程中误差综合考虑高程注记点的测量精度和地形因素造成的影响,计算公式为

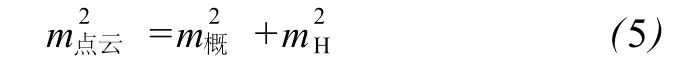
本例以 1：500的数字地形图作为参考,根据规程[8]中对高程精度的要求,高程注记点的高程中误差mH为 0.4 m。地形概括误差的计算公式为：

式中,m概为地形概括中误差,L为地形点间距,μ为地形概括系数(平地取 0.04,丘陵地取 0.15,山地取 0.25,高山地取 0.30)。计算得出 m概远小于mH。综上所述,阈值设定为 0.4 m。

为了验证该去噪算法的可行性,利用 Ti mble GX200地面三维激光扫描系统获取的某矿区地形扫描数据作为实验对象进行分析,并根据该区原始数字化地形图,提取测站附近 48个高程注记点作为先验信息,利用可视化编程语言 visual basic实现了去噪(图1)。

分析图 1可知,去噪前的地形有明显的树木、电线杆和建筑物,而去噪后基本为平面,可见该去噪算法能够基本上去除地表噪声点。但从去噪前后的点云数量来看,仅仅去除了较为明显的噪声点,对于地面上细小的噪声点没有完全去除。

2.2 基于高程注记点拟合平面的去噪算法

在基于高程注记点内插高程值的去噪算法中,用高程注记点内插点云的理论高程值,通过比较理论高程与实测高程的不符程度剔除噪声。这种方法虽然思路合理并且实现起来较为简单,但在实际应用中往往会受到系统误差的影响,内插高程值不能准确与点云的实际高程值严格相符。基于高程注记点拟合平面的去噪算法克服了上述系统误差的影响,其原理是建立栅格数据模型来模拟真实地表[9],并以拟合的局部平面与地表的夹角作为判断依据去除噪声。

算法基本思路如下：

首先利用规则格网将点云数据分块,其边长的选择主要取决于其内的扫描点个数。计算时只要每个格网中有 3个以上扫描点就能满足要求,若格网划分过大会对地表变化不敏感,在整格剔除中也会去掉过多的地表扫描点。因此,理论上格网划分的越细密精度越高,去噪效果也越显著。然而实际应用中若划分过于细小会耗费大量时间,在精度要求不高的情况下是没有必要的,因此应根据实际情况选取适当的格网边长。

其次在格网范围内,利用最小二乘法拟合平面[10]。平面方程一般表达式为：

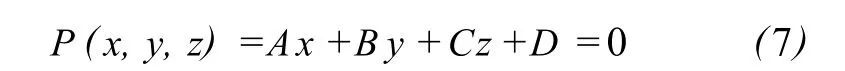
对格网内的点云数据 (xi,yi,zi)(i=0,1,…, m),要求其最小二乘拟合平面满足：

最后判断利用高程注记点内插扫描点高程后具有的理论值拟合而成的平面,与扫描点拟合而成平面所成的二面角是否超过规定的阈值,若所成的二面角过大,则说明格网内的点中有明显噪声,使其拟合的局部平面与地表变化趋势不符,则应剔除。当已知两平面的法向量为 n1=(A1,B1,C1)、n2=(A2, B2,C2),夹角θ的计算公式为：

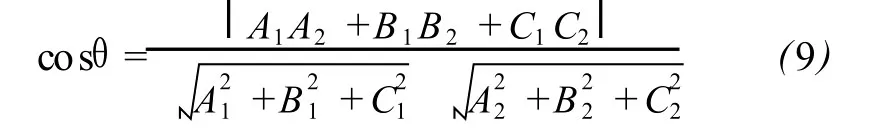
图1 去噪前后对比Fig.1 Comparison between the images before and after noise elimination

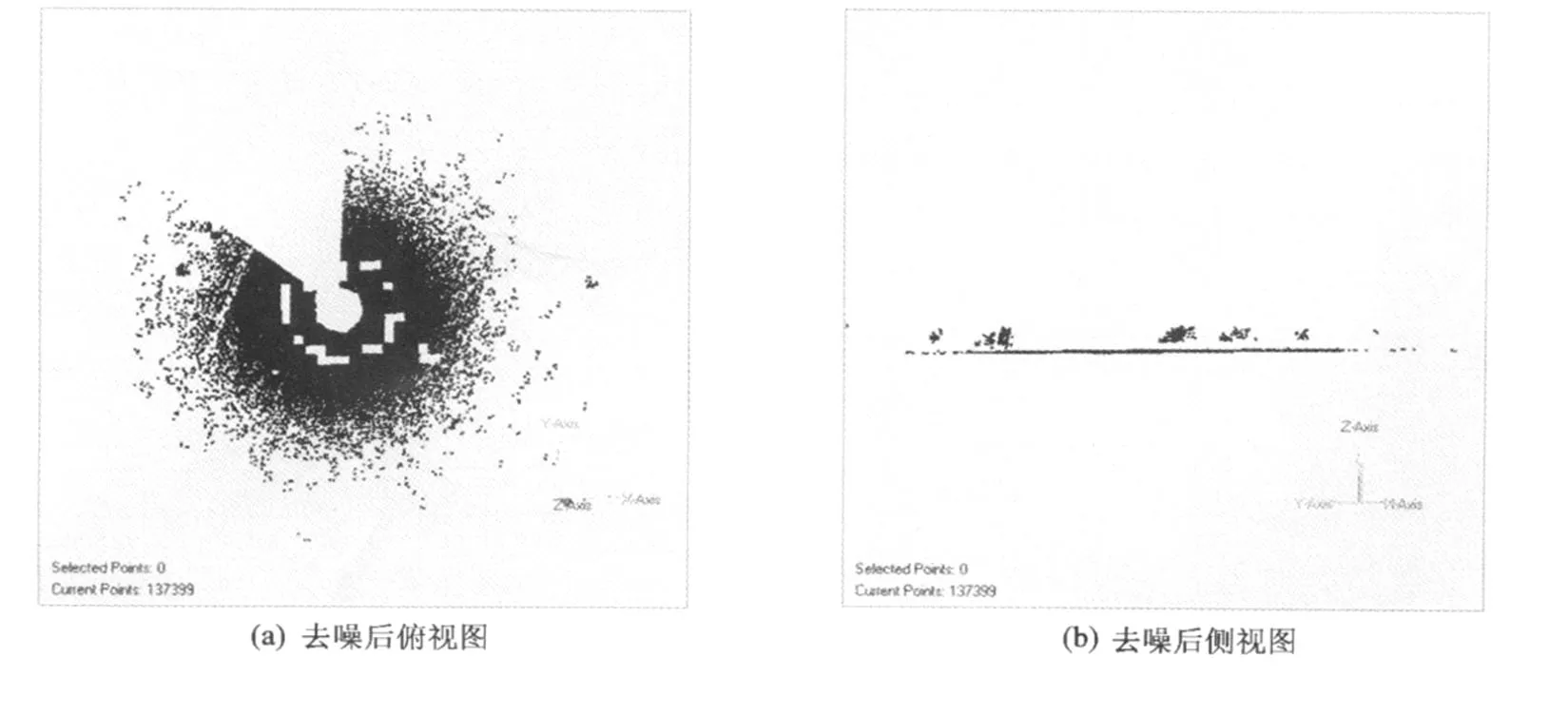
图2 去噪后效果Fig.2 Results after noise eli mination

图2为基于高程注记点内插高程值的去噪算法得到的去噪效果图。从图 2可知,第一次去噪后,虽然散乱分布的明显噪声点以及树冠等离地面较大的点没有完全剔除,但是贴近地表的植被、电线杆和建筑物立面已基本上剔除。之所以会出现上述现象,是由于树冠枝叶密集,导致所选区域内的点恰好拟合出与地表几乎平行的平面。而树木的枝干、电线杆、建筑物的立面等,基本垂直于地面,很容易剔除。

用本算法剔除后将噪声点与地面点明显区分开,使得下一步手工剔除变得简单易行。本例中在利用该算法剔除后,再次利用点距法剔除了剩余的噪声,效果如图 3。

图3 再次去噪后的点云Fig.3 Point clouds after second noise elimination

2.3 基于高程注记点拟合趋势面的去噪算法

在基于高程注记点拟合平面的去噪算法中,要想利用拟合局部平面反映地表的起伏状况,就要划分较为密集的格网以逼近真实地表,而密集格网在运算过程中会耗费大量的时间。如果能直接用高次方程建立地表的曲面模型,一方面更符合地表的实际情况,另一方面可以大幅增加格网边长,从而节省运算时间。然而建立曲面模型之后若以角度作为去噪指标不易实现,需要寻求其他指标作为判断依据。

算法基本思路如下：

首先划分规则格网,根据高程注记点的密度划分格网以保证格网中至少有 6个高程注记点。

然后利用最小二乘原理分别拟合局部曲面[11]。曲面方程一般表达式为：

对格网内的点云数据 (xi,yi,zi)(i=0,1,…,m),要求其最小二乘拟合平面满足：

最后将扫描点的平面坐标 (xk,yk)代入曲面方程中求得拟合高程值对比与 zk的差值,若 Δzk超过设定的阈值则作为噪声点剔除,否则保留。阈值的选取需根据曲面拟合的精度设定,通常认为Δzk为测量过程中由各种因素影响而成的综合误差,按照公式(12)计算出拟合中误差后取 2倍中误差作为阈值。

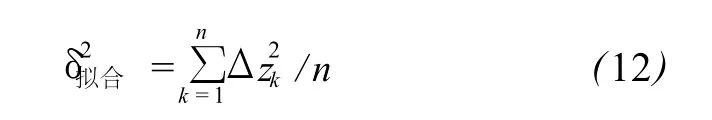
图4为基于高程注记点拟合平面的去噪算法得到的效果图。由图 4可知,该算法能够有效地剔除地表噪声,去噪效果明显,但也仅除去了较明显噪声(图 5),对于地表细小噪声点没有完全去除。

3 算法对比分析

图4 去噪后效果Fig.4 Results after noise eli mination

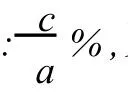
由表 1和表 2可知,未采取先验信息的去噪虽可以将噪声基本去除,但总误差较大,不能很好地符合实际地形。

此外,方法一与方法三的存真误差极小,且经过这两种方法处理后,数据中的明显噪声基本剔除,不足之处在于纳伪误差较大,说明地表附近仍留有大量微噪声。从运算效率来看,方法一需逐点内插点云高程,计算速度较慢。方法二纳伪误差较小,说明利用该方法去噪后更接近真实地表,结合去噪后的数据分布比例来看,地表附近的微噪声基本剔除,但有少量明显噪声残留,需要进一步手工剔除。

图5 噪声点Fig.5 Noise points

表1 几种去噪方法误差的比较Tab.1 Comparison among the errors with different noise eli m ination algorithm s

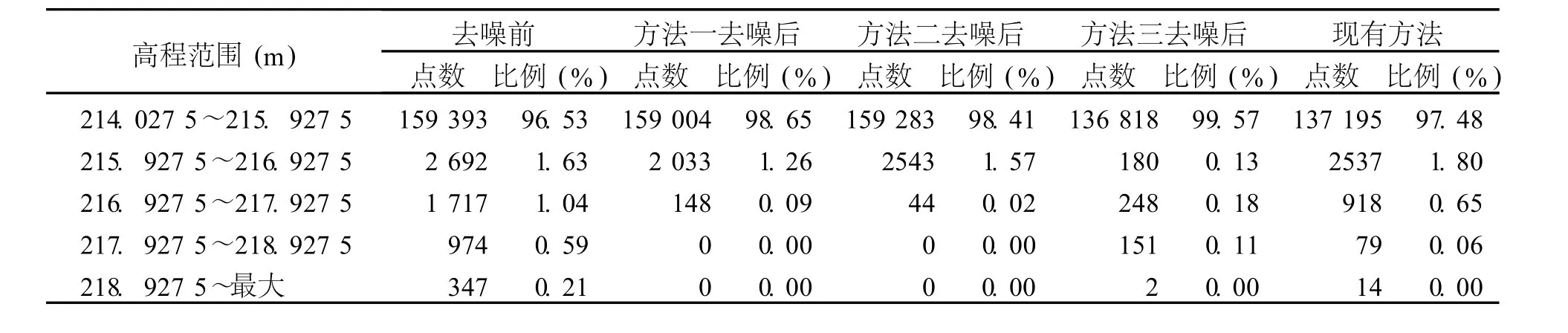
表2 去噪前后点云的分布Tab.2 D istribution of poi nt clouds before and after noise eli mation

4 结论

本文结合原有地形图提供的宏观信息作为先验知识,使得去噪后的扫描数据更加符合实际情况。对 3种去噪方法进行的实例对比分析结果表明,高程注记点确实可以作为先验信息为点云去噪提供依据,较现有方法具有明显优势。在实际测量中不具备原始地形图的情况下,也可预先利用 RTK测出一定数量的地表点代替高程注记点作为先验信息。在指标的选取上,可以选择内插高程值、拟合平面或趋势面进行对比。相比而言,选择内插高程值或拟合趋势面作为指标适用于去除明显噪声或精度要求不高的情况,而拟合平面去噪算法克服了系统误差影响,去噪更为精确。此外,从运算速度来看,拟合趋势面去噪算法具有明显优势。

1 梅文胜,周艳芳,周俊.基于地面三维激光扫描的精细地形测绘 [J].测绘通报,2010,(1)：53-56.(Mei Wensheng,Zhou Yanfang and Zhou Jun.Fine topographic mapping based on ground thre-dimensional laser scanning [J].Bulletin of Surveying and Mapping,2010,(1)：53-56)

2 Killian J,Haala N and Englich M.Capture and evaluation of airborne laser scanner data[J].International Archives of Photogrammetry and Remote Sensing,1996,31：383-388.

3 Axelsson P.DEM generation from laser scanner data using adaptive TI N models[J]. International Archives of Photogrammetry and Remote Sensing,2000,33：110-117.

4 Kraus K and Pfeifer N.Determination of terrain models in wooded areas with airborne laser scanner data[J]. ISPRS Journal of Photogrammetry and Remote Sensing,1998,53 (4)：193-203.

5 Sithole G and Vosselman G.Filtering of laser altimetry data using a slope adaptive filter[J]. International Archives of Photogrametry and Remote Sensing,2001,34：203-210.

6 张小红,刘经南.机载激光扫描测高数据滤波[J].测绘科学,2004,29(6)：158-160.(Zhang Xiaohong and Liu Jingnan.Airborne laser scanning altimetry data filtering[J]. Science of Surveying andMapping,2004,29(6)：158-160)

7 Vosselman G.Slope based filtering of laser altimetry data [J].International Archives of Photogrammetry and Remote Sensing,2000,33：935-942.

8 GB/T18315-2001,数字地形图系列和基本要求[S].北京：中国标准出版社,2001.(GB/T18315-2001,Series and basic requirements of digital topographic maps[S].Beijing： Standards Press of China,2001)

9 李清泉,等.三维空间数据的实时获取、建模与可视化[M].武汉：武汉大学出版社,2003.(LiQingquan,et al. Realti me acquisition,modeling and visualization of 3D spatial [M].Wuhan：Wuhan University Press,2003)

10 蔡来良,吴侃,张舒.点云平面拟合在三维激光扫描仪变形监测中的应用[J].测绘科学,2010,35(5)：231 -232.(Cai Lailiang,Wu kan and Zhang Shu.Application of point cloud plan fitting to deformation monitoring using 3D Laser scanner[J].Science of Surveying and Mapping, 2010,35(5)：231-232)

11 朱长青.计算方法及其在测绘中的应用[M].北京：测绘出版社,1997.(Zhu Changqing.Calculation method and its application in surveying and mapping[M].beijing：Surveying andMapping Press,1997)

12 张皓,等.一种基于平面拟合的 L I DAR点云滤波方法[J].测绘科学,2009,34(4)：141-143.(Zhang Hao, et al.A method for filtering L I DAR points cloud based on plannar fitting[J].Science of Surveying and Mapping, 2009,34(4)：141-143)

13 Sithole G and Vosselman G.Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds[J]. ISPRS Journal of Photogrammetryamp;Remote Sensing,2004,59：85-101.

NO ISE EL I M INATI ON ALGORITHM S FOR TERRESTRIAL 3D LASER SCANNING DATA W ITH PRI ORI INFORMATI ON

Zhao Xin1,2),Wu Kan1,2)and CaiLailiang1,2)

(1)Jiangsu Key Laboratory of Resources and Environm ental Infor m ation Engineering,Xuzhou 221116 2)School of Environm ent Scienceamp;Spatial Infor m atics,CUM T,Xuzhou 221116)

In order to avoid the distortion of the real situation reconstruction,and on the basis of related theory of noise removing,some researches are taken and three noise elimination algorithms for terrestrial 3D laser scanning data with priori infor mation,utilizing the points labled with height as the priori infor mation are presented,elevation of interpolation,fitting plane or trend surface with Least-square method being compared,and choice of proper threshold to eli minate noise.The experi mental results indicate that points labled with height can be used as standard of noise eli mination for the entity features are well preserved.

laser scanning;noise;priori-information;elevation interpolation;planner fitting

赵 鑫1,2)吴 侃1,2)蔡来良1,2)

(1)江苏省资源环境信息工程重点实验室,徐州 221116 2)中国矿业大学环境与测绘学院,徐州 221116)

1671-5942(2011)04-0107-06

2011-01-21

国家环保公益性行业专项(200809128);江苏省“青蓝工程”项目

赵鑫,女,1986年生,硕士研究生,主要研究方向为三维激光扫描数据分析处理.E-mail：zhaoxin860726@126.com

P237;P207

A