加权总体最小二乘方法在 ITRF转换中的应用＊

陆 珏 陈 义 郑 波

(1)同济大学测量与国土信息工程系,上海 200092 2)现代工程测量国家测绘局重点实验室,上海 200092 3)上海市地籍事务中心上海市土地登记事务中心,上海 200003)

加权总体最小二乘方法在 ITRF转换中的应用＊

陆 珏1)陈 义1,2)郑 波3)

(1)同济大学测量与国土信息工程系,上海 200092 2)现代工程测量国家测绘局重点实验室,上海 200092 3)上海市地籍事务中心上海市土地登记事务中心,上海 200003)

针对 ITRF转换中,两套坐标系下的点坐标值均存在误差,且各点之间精度不等、甚至相关的情况,提出利用加权总体最小二乘方法对转换参数进行解算。通过模拟数据和真实数据的解算证明了加权总体最小二乘方法在 ITRF转换中的适用性,与其他方法相比,利用加权总体最小二乘方法能够得到准确的、更为合理的转换参数。

加权总体最小二乘(WTLS);误差(EI V)模型;协因数阵;坐标转换;布尔莎模型

1 引言

总体最小二乘方法在求解观测方程 Ax=b时,除了按经典最小二乘方法求解时要考虑观测向量 b的误差外,还需考虑系数矩阵 A的误差[1,2]。系数矩阵与各种模型改正、先验信息的误差有关,因此,总体最小二乘法相对于最小二乘法而言更合理和完整。

近年来,Schaffrin对约束总体最小二乘法的计算方法[3]、线性回归加权总体最小二乘法的计算方法[4]、以及附有线性和二次约束条件的总体最小二乘法的计算方法[5]进行了探讨。同时,在总体最小二乘方法的应用方面,Felus[6]和 Schaffrin[7,8]分别讨论了基准转换中系数矩阵存在误差时,如何合理地确定基准转换的参数,不过,他们讨论的仅仅是 2维的情况,并且认为两个坐标系统的坐标服从相同的误差分布,且各个误差相互独立。陆珏[9]和陈义[10]讨论了三维线性基准转换、空间后方交会的总体最小二乘估计方法,但解算时也认为误差服从相同的分布,且相互独立。

在 ITRF转换的观测方程中,观测向量 b和系数矩阵A分别由目标坐标系和原坐标系下的点坐标值构成。这些点不仅都存在误差,且由于观测手段、观测距离、网型结构等原因使得它们的精度并不相等,且存在相关。

为了同时考虑观测向量和系数矩阵的误差,以及它们之间的不等精度和相关性,本文采用加权总体最小二乘 (WTLS)方法来解算 ITRF转换问题。在对该方法原理和算法研究的基础上,通过对模拟数据和 ITRF2005至 ITRF2000真实坐标转换数据进行计算,并与加权最小二乘(WLS)方法和总体最小二乘(TLS)方法的计算结果进行比较,证明了利用WTLS方法计算 ITRF转换参数能够得到准确的、更合理的结果。

2 加权总体最小二乘方法

在变量误差 (EI V)模型中,观测向量 b和系数矩阵A均包含随机误差,因此观测方程可定义为[]：

观测向量 b∈Rn×1,它包含着 e。参数向量 x∈Rm×1。系数矩阵 A∈Rn×m,其中 n＞m=rank(A)。EA代表存在于 A阵中的随机误差矩阵,在最小二乘中 EA≡0[11]。

可见,与仅考虑观测值向量 b中的误差、忽略系数矩阵A中误差的LS方法相比,TLS方法关心的则是当观测向量 b和系数矩阵A中都含有误差,需要同时平差的参数估计问题。

进一步地,随机误差 e和 EA的数字特征可表示为：

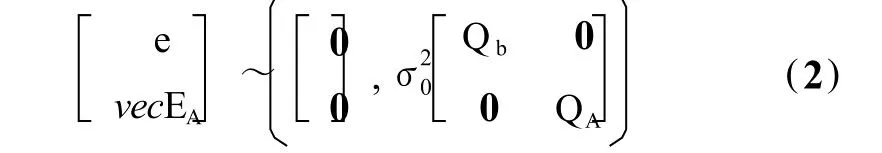
“vec”是指将矩阵从左至右按列拉直所得到的列向量,这里定义 vecEA=eA。为单位权方差,Qb和QA分别为 e和 eA的权逆阵,可表示为：

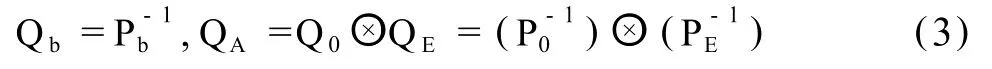
Q0∈Rm×m,QE∈Rn×n,⊗代表的是矩阵之间的直积,即“Kronecker-Zehfuss积”,具体表现为：M⊗N：=[mijN],M=[mij]。通过矩阵间的直积,可以得到系数矩阵A中误差的权逆阵。此时,WTLS方法的目标函数为：

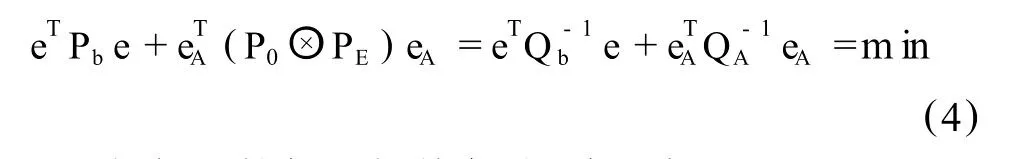
根据拉格朗日极值条件,建立方程：

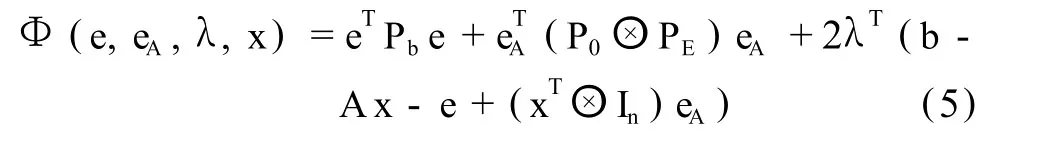
其中λ为拉格朗日乘算子,EAx=(xT⊗In)eA。在拉格朗日条件方程的基础上,对方程中的每个参数进行求导解算,最终可以得到WTLS方法的解算过程为[4]：

第一步,解算初值：

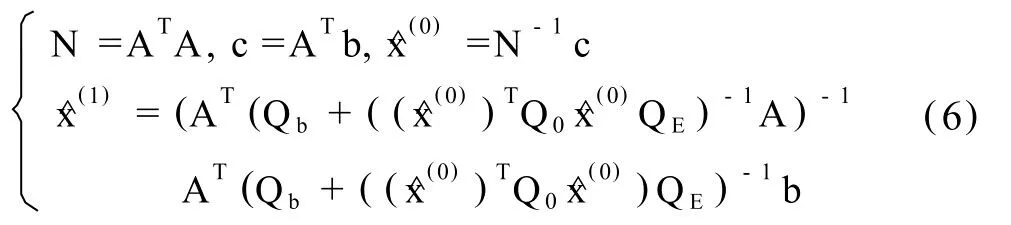
第二步,迭代解算：

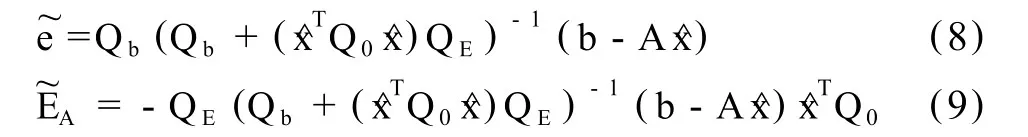
有偏的单位权方差为：

3 加权总体最小二乘方法在 ITRF转换中的应用

两个不同时间下的 ITRF转换是一个小角度的三维坐标转换,若对原坐标系和目标坐标系下的点坐标都进行重心化,则可以将平移参数略去,只解算尺度参数和旋转参数[12]。因此重心化后,新旧坐标系重心化后的布尔莎模型可表示为：其中 (x2i,y2i,z2i)为第 i个控制点在目标坐标系下的坐标,它们组成了观测向量 b。(x1i,y1i,z1i)为对应点在原坐标系下的坐标,它们构成了系数矩阵A中的变量。这里共有 k个对应点。μ、(εx,εy,εz)分别为坐标转换参数中的 1个尺度参数以及 3个分别对x轴、y轴和 z轴的旋转角参数。

对于具有 k个已知点的三维坐标转换观测方程而言,n=3k,m=4,Q0=I4×4。令原坐标系下各点坐标之间的协因数阵为：

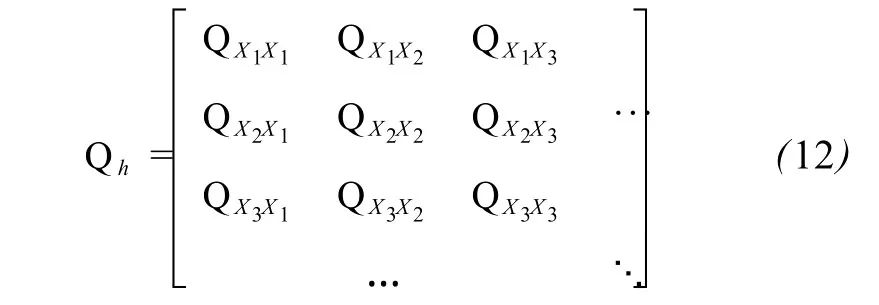
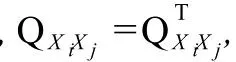
若已知原坐标系和目标坐标系下各点之间的方差协方差阵,则Qorg(Qorg∈R3k×3k)和Qb已知。下面介绍如何解算QE：

由于

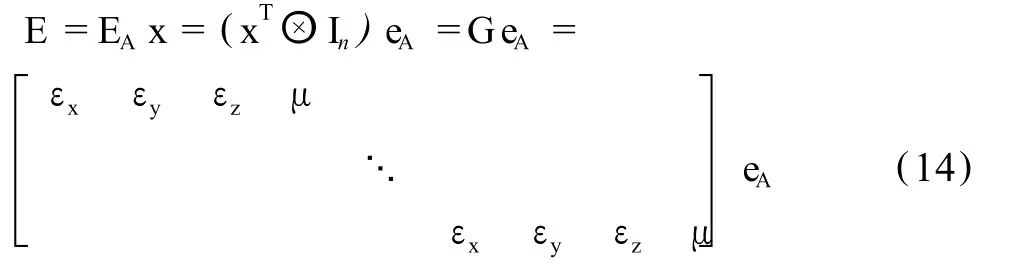
G∈Rn×4n,由协因数传播定律[13]可知：

通过系数矩阵 A中逐个元素对原坐标系下每个点的三维坐标进行求导得到：

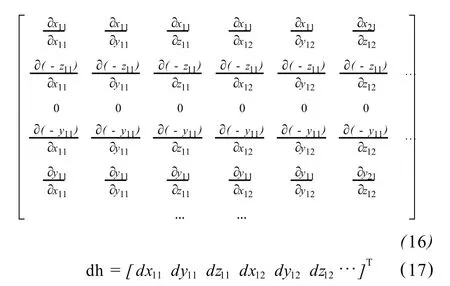
γ∈R4n×n,可见 eA=γdh,根据协因数传播定律[13]：

因此,将式 (12)和 (16)代入式 (18)可得 QeA,再将QeA代入式 (15)即可计算出矩阵 QE。而对于式(15)的矩阵 G中的坐标转换参数可先由WLS方法求出,之后再由WTLS方法不断迭代更新代入解算。

4 计算步骤与算例

4.1 计算步骤

应用WTLS方法进行 ITRF的转换可以按以下步骤实现：

1)对两套坐标系下的点坐标进行重心化;

2)根据目标坐标系下点坐标的方差协方差阵Qb计算观测向量 b的权矩阵 Pb;

3)利用WLS方法根据式 (11)解算出坐标转换参数初值,从而计算式(15)中的矩阵 G;

4)根据原坐标系下各点坐标的协因数阵列出Qh,如式 (12)、(13)所示;

5)由式 (16)计算γ,并将γ和 Qh代入式 (18)计算QeA;

6)将步骤 3)和 5)计算出的 G和 QeA代入式(15)得到 QE;

7)由式(6)和(7)计算 ITRF转换参数的WTLS解,再次带入式(15)更新 G和QE的值;

8)最后,由式 (8)和式 (9)分别计算观测向量和系数矩阵的改正数,并由式(10)计算WTLS的单位权方差。

4.2 算例

为了验证上述算法的正确性,分别利用模拟数据和实际数据,采用WLS、TLS和WTLS方法进行计算,并从参数估值、单位权中误差等几个方面对结果进行对比和分析。

例 1 先采用模拟三维小角度坐标数据进行解算,两套坐标系下对应点的坐标如表 1所示。

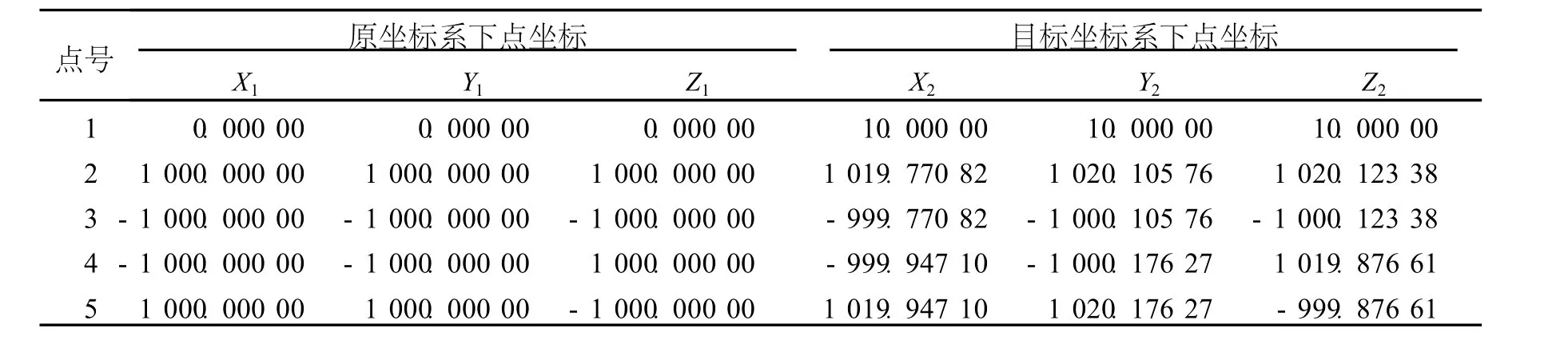
表1 原坐标系和目标坐标系下对应点的坐标(单位:m)Tab.1 Coordi nates of corresponding poi nts in two coordi nate system s(un it:m)

表1中,模拟的坐标转换参数为 (x0,y0,z0)= (10,10,10),μ=1.01,(εx,εy,εz)=(0.05°,0.02°, 0.08°)。为了验证WTLS方法能够准确地反应出两套坐标系下点的误差情况,并进行改正,采用了1 000组模拟数据。

第一次,对原坐标系及目标坐标系下点的 X、Y、Z坐标值分别加入单位权中误差为 1 mm、均值为零,和单位权中误差为 1 cm、均值为零的随机误差。WTLS方法计算出的观测向量单位权中误差和系数矩阵的单位权中误差见图 1和图 2。

图1和图 2所表示的观测向量单位权中误差和系数矩阵的单位权中误差均值分别为 0.988 2 cm和 0.983 mm,与加入的误差相匹配。

利用WLS、TLS和WTLS方法计算出的坐标转换参数平均值和模拟的坐标转换参数之差如表 2所示。

由表 2可看出,相比于WLS和 TLS方法,利用WTLS计算的结果更加接近模拟值。

第二次,对原坐标系及目标坐标系下点的 X、Y、Z坐标值分别加入单位权中误差为 5 mm、均值为零,和单位权中误差为 2 cm、均值为零的随机误差。

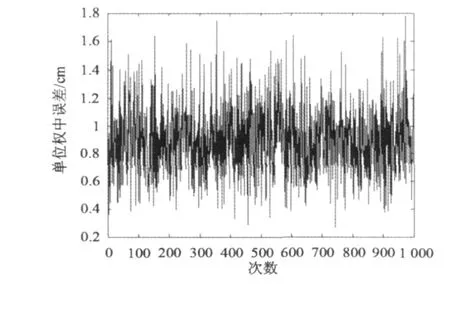
图1 WTLS方法估计的观测向量的单位权中误差(方案1)Fig.1 Unit weight mean square error of observation vector estimated byWTLS solution(caseⅠ)

此时,WTLS方法计算出的观测向量单位权中误差和系数矩阵的单位权中误差分别如图 3和图 4所示。

图3和图 4计算的观测向量单位权中误差和系数矩阵的单位权中误差均值分别为 1.960 1 cm和4.907 nn,同样与加入的误差相匹配。

再次利用WLS、TLS和WTLS方法计算坐标转换参数平均值和模拟值之差如表 3所示。

表3的结果再次证明了利用WTLS方法不仅可以准确地计算出坐标的转换参数,且结果更加接近模拟值。

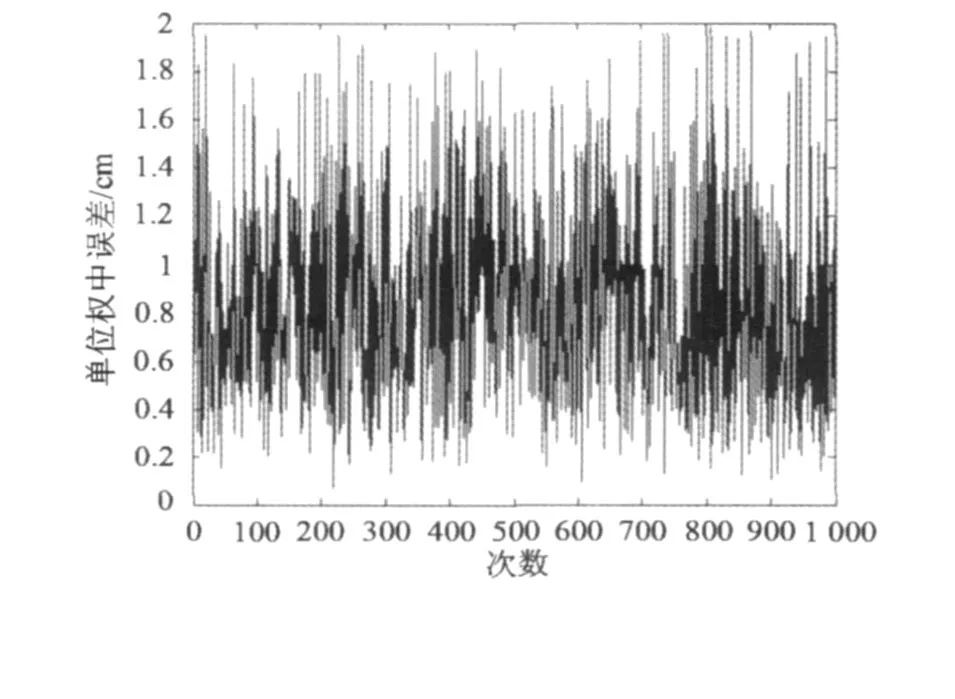
图2 WTLS方法估计的系数矩阵的单位权中误差(方案1)Fig.2 Unit weight mean square error of coefficient matrix estimated byWTLS solution(caseⅠ)

表2 由WLS、TLS和W TLS方法计算出的坐标转换参数与模拟值之差Tab.2 D ifferences of transformation parameters between calculation results and si mulation values

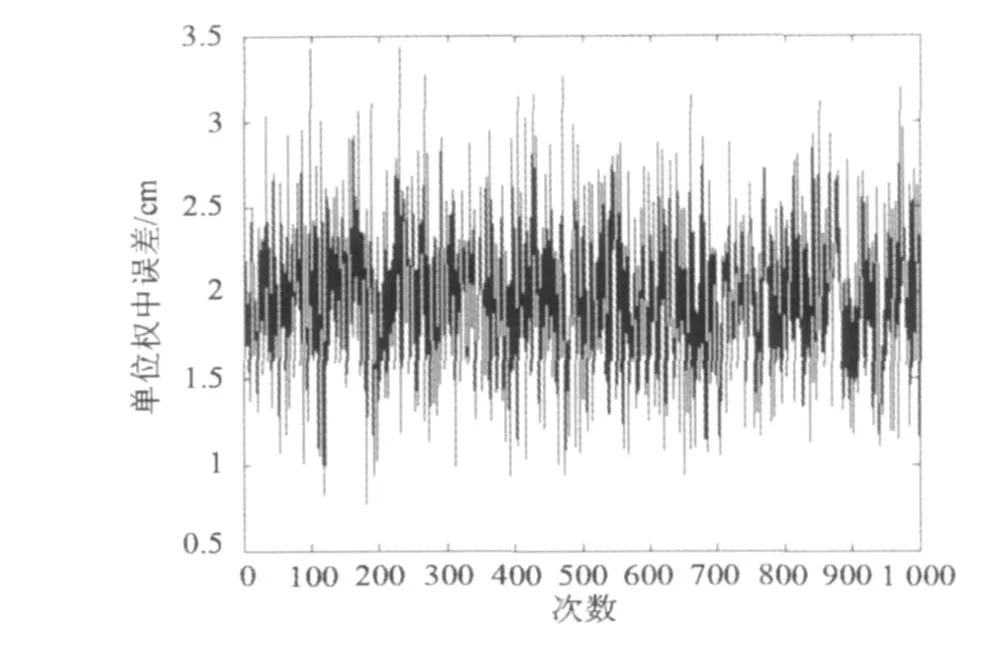
图3 WTLS方法估计的观测向量的单位权中误差(方案2)Fig.3 Unit weight mean square error of observation vector estimated byWTLS solution(caseⅡ)

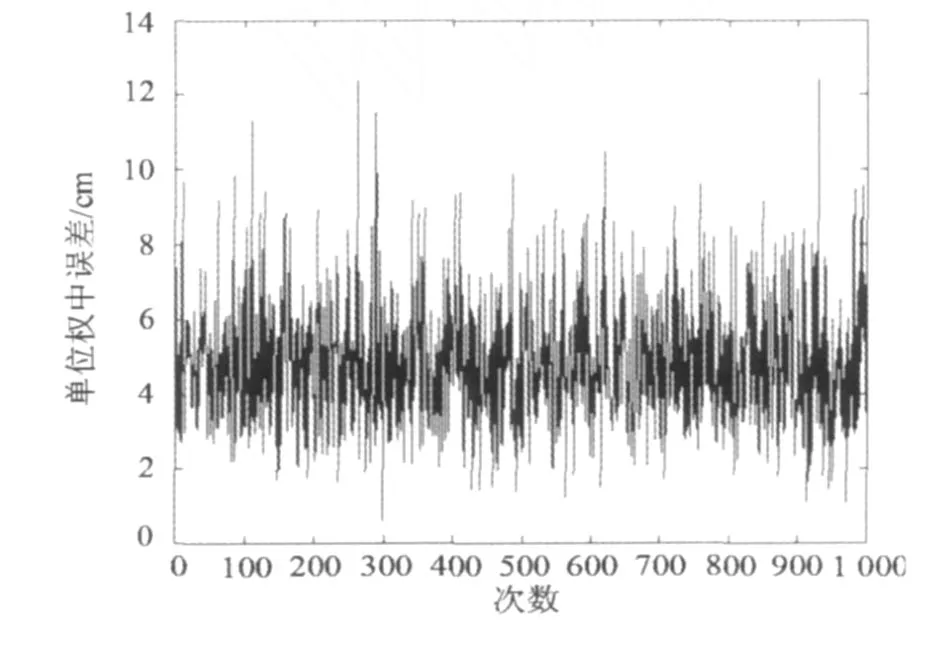
图4 WTLS方法估计的系数矩阵的单位权中误差(方案2)Fig.4 Unit weight mean square error of coefficient matrixestimated byWTLS solution(caseⅡ)

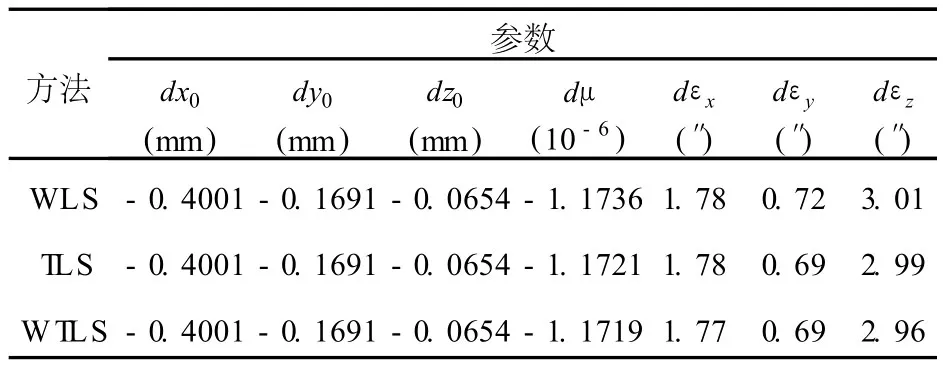
表3 由WLS、TLS和W TLS方法计算出的坐标转换参数与模拟值之差Tab.3 D ifferences of transformation parameters betweencalculation results and si mulation values

而从图 1至图 4的结果可以看出,当给两套坐标系下的点坐标值分别加入不同量级的误差时, WTLS计算出的 e和 EA都能够准确地予以反应。

例 2 采用国际地球自转服务(IERS)网站上公布的全球较稳定的 70个站点在 ITRF2005以及ITRF2000坐标框架下的坐标、速度以及它们之间的方差协方差阵,分别采用WLS、TLS和WTLS方法进行计算。3种方法的计算结果以及与网站公布的坐标转换参数见表 4,其中,D=μ-1。

表4 WLS、TLS以及W TLS计算坐标转换参数结果Tab.4 Comparison among transformation parameters calculated byWLS,TLS andW TLS solutions

可以看出,相比WLS和 TLS方法,利用WTLS方法计算出的坐标转换参数与 IERS网站公布的结果更接近。而WLS和WTLS方法计算的单位权中误差分别为 1.498 51和 1.342 82,这也再次证明了WTLS方法可以对 EI V模型进行合理的解算,从而计算出正确的、精度更高的坐标转换参数。

5 结论

1)总体最小二乘方法不仅顾及观测向量中的误差,而且顾及包含变量的系数矩阵中的误差,因此理论上更加严密,估计效果更佳,可用于 ITRF转换的计算中;

2)当观测向量以及系数矩阵中的各元素不等精度、甚至相关时,应用WTLS方法解算 ITRF转换参数更为合理;

3)通过模拟数据的计算可以看到,WTLS方法能够对原坐标系和目标坐标系下点的误差分别改正,且改正量与加入的误差相符合。

1 Golub H G and Van Loan F C.An analysis of the total least squares problem[J].SI AM Journal on Numerical Analysis, 1980,17(6)：883-893.

2 魏木生.广义最小二乘问题的理论和计算[M].北京：科学出版社,2006.(WeiMusheng.Generalized least squares theory and calculation[M].Beijing：Science Press,2006)

3 Burkhard Schaffrin.A note on constrained total leastsquares estimation[J].LinearAlgebra and itsApplications, 2006,417：245-258.

4 Schaffrin B andW ieserA.On weighted total least-squares adjust ment for linear regression[J].Journal of Geodesy, 2008,82,415-421.

5 Schaffrin B and Felus Y A.An algorithmic approach to the tatal least-squares problem with linear and quadratic constraints[J].Stud Geophys Geod.,2009,53：1-16.

6 Yaron A and FelusBurkhard Schaffrin.Perfor ming similarity transformations using the error-in-variables model[R]. ASPRS 2005 Annual Conference Balti more,Maryland, March 7-11,2005.

7 Schaffrin B and Felus YA.On the multivariate total leastsquares approach to empirical coordinatetransformation：Three algorithms[J].J Geodesy,2008,82：373-383.

8 SchaffrinB,et al.Total least-squares for geodetic straightline and plane adjustment[J].Boll Geod Sci Aff.,2006, 65：141-168.

9 陆珏,陈义,郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学,2008,(5)：77-81.(Lu Jue,Chen Yi and ZhengBo.Research study on three -dimensional datum transformation using total least squares [J].Journal of Geodesy and Geodynamics,2008,(5)：77 -81)

10 陈义,陆珏,郑波.总体最小二乘方法在空间后方交会中的应用[J].武汉大学学报 (信息科学版),2008,33 (12)：1 271-1 274. (Chen Yi,Lu Jue and Zheng Bo. Application of total least squares to space resection[J]. Geomatics and Information Science of Wuhan University 2008,33(12)：1 271-1 274)

11 Van Huffel S and Vandeualle J.The total least squares problem[J].Computational Aspects and Analysis,Frontiers in Applied,Mathematics,1991,(9)：1-87.

12 Shen Y Z,Chen Y and Zheng D H.A quaternion-based geodetic datum transformation algorithm[J]. Springer-Verlag J Geod,2006,80：233-239.

13 樊功瑜.误差理论与测量平差[M].上海：同济大学出版社,1998.(Fan Gongyu.Error theory and surveying adjustment[M].Shanghai：TongjiUniversity Press,1998)

APPL ICATI ON OFW EIGHTED TOTAL LEAST SQUARES IN ITRF TRANSFORMATI ON

Lu Jue1),Chen Yi1,2)and ZhengBo3)

(1)The Departm ent of Surveying and Geo-infor m atics,Tongji University,Shanghai 200092 2)Key Laboratory of Advanced Surveying Engineering of SBSM,Shanghai 200092 3)Shanghai CadastreM aragenent Center,Shanghai 200003)

According to the fact that the points in two transformational coordinate systems are all affected by random errors,which make the observation vector and coefficientmatrix in error equations both include errors,and even,these observations and elements in coefficient matrix may be heteroscedastic and correlated.We employ the weighted total least squares solution to calculate the parametersof ITRF transformation.To demonstrate the performance and efficiency of the application ofWTLS solution in coordinate transformation,the simulation and real experiments are i mplemented.The results show that theWTLS solution is correct and more reasonable.

weighted total least squares;errormodel;cofactormatrix;coordinate transformation;Bursa model

1671-5942(2011)04-0084-06

2011-01-24

国家自然科学基金(41074017)

陆珏,女,1985年生,博士生,研究方向：测量数据处理、摄影测量.E-mail：lujue1985@126.com

P207

A