天文大气折射的级数展开式*
2011-11-23张捍卫丁安民雷伟伟
张捍卫 丁安民 雷伟伟
(河南理工大学测绘学院,焦作 454003)
由于ξ2的量级是 10-2,ξ4的量级是 10-4。因此有:
天文大气折射的级数展开式*
张捍卫 丁安民 雷伟伟
(河南理工大学测绘学院,焦作 454003)
对天文大气折射的级数展开理论进行了研究,给出了新的级数展开式。新的级数展开式能够展开到任意阶次项,并且达到了亚毫角秒的理论精度;另外,把地面附近的位相折射指数作为未知数单独提出来,适应了光学技术在不同观测波长情况下的处理,并给出了以视天顶距正切为引数的级数展开式。这一成果将可完全取代普尔科沃大气折射表公式,也可以利用该方法进行射线跟踪的理论研究。
天文大气折射;级数展开式;大气折射指数;亚毫角秒精度;普尔科沃大气折射表公式
1 引言
早在公元 1世纪,人们就已认识到大气折射现象。但直到公元 17世纪,才逐渐创立了大气折射理论。之后,很多著名学者,例如欧拉、拉格朗日和拉普拉斯等都研究过大气折射。俄罗斯普尔科沃天文台一直从事天文大气折射表的编制工作,其理论依据是基里金在 1866—1873年期间的研究工作。1870年,普尔科沃天文台编制的大气折射表问世,几乎替代了当时的所有折射表。以后几经改进,被誉为当时最精确的大气折射表并得到广泛采用[1]。20世纪 40年代以后,发展起来的其他大气折射理论也起了很重要的作用[2-4]。文献[5,6]把 1天文大气折射的被积函数以视天顶距为引数进行级数展开,在确定大气分布模型基础上进行积分,给出了一个新的级数展开式,并在其后得到了广泛应用。相对目前观测技术水平来说,该工作存在如下问题:级数展开只取到有限的几阶,且其系数只保留到角秒量级;地面附近的位相折射指数作为特定波段的数值被包含于级数展开的系数中,不利于不同波段的处理;在级数展开的过程中,视天顶距没有以显函数的形式给出。目前,大气折射研究已考虑到大气模型与其折射指数理论公式的不对应性[7],以及能够与测站周围地理环境相适应的实际大气模型的分布,例如文献[8]给出了直接测定瞬时天文大气折射值的一种有效方法,并建立了适应于云南天文台本地的、随方位和光谱型而异的天文大气折射模型。
本文将在文献[5,6]的理论基础上,对天文大气折射级的数展开理论进行重新研究。
2 天文大气折射的级数展开式
无穷远平面电磁波到达地面测站时,其真天顶距ξ与视天顶距ξ0的关系为[5,9]:

式中,Δz称为天文大气折射 (或蒙气差),在球对称大气模型假设下,其基本微分方程是[5,9]:

式中,n、ξ和 r分别是传播路径上某点的大气位相折射指数、视天顶距 (平面电磁波传播方向与该点地心向经的夹角)和地心距;n0和 r0分别是测站点的大气位相折射指数和地心距。令

根据式(3)可得

假设取中性大气层顶的高度为 72 km左右,此处的位相折射指数约为 (n-1)≈6.0×10-9。如果只考虑中性大气层对蒙气差的影响,有
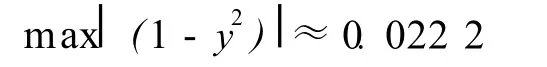
因此,如果要使得

那么就必须要求视天定距满足ξ0≤81.5°。在此要求下对式(5)进行展开,即

其中约定
(2k-1)!! =1·3·5…(2k-1);且(-1)!! =1
(2k)!! =2·4·6…(2k);且 (0)!! =1如果定义数组
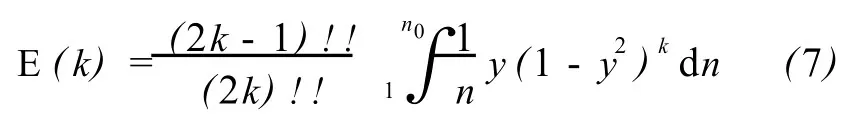
那么根据式(2)、(6)和(7)可得

如果能够得到数组 E(k)的具体数值,那么式 (8)就是天文大气折射的级数展开式。
2 亚毫角秒理论精度的级数展开
假设 tanξ0的量级大小是 10,则根据式 (8)可见,如果要使得每一项都能保留到亚毫角秒量级的大小,那么 E(k)的数值必须取到 10-2k-10。假设(n0-1)的量级是 10-4,那么根据式 (7)可知,y(1-y2)k的数值必须取到 10-2k-6。令

由于ξ2的量级是 10-2,ξ4的量级是 10-4。因此有:

则

或者

利用二项式展开
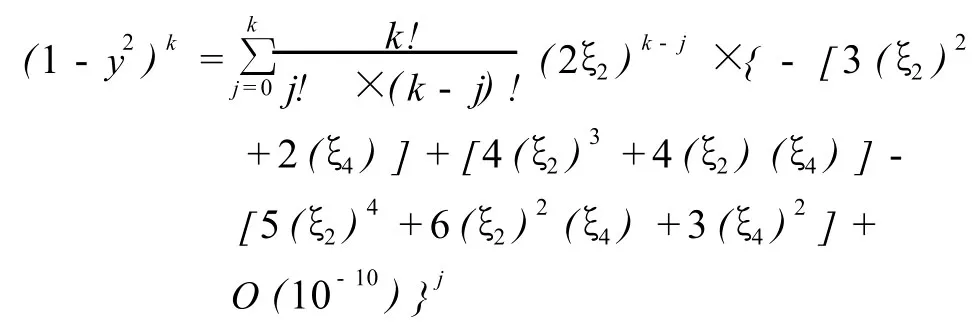
可见,取 j=0、1、2、3的情况下,就能使得 (1-y2)k保留到 10-2k-6的量级。因此,利用以上相关公式在此量级上有
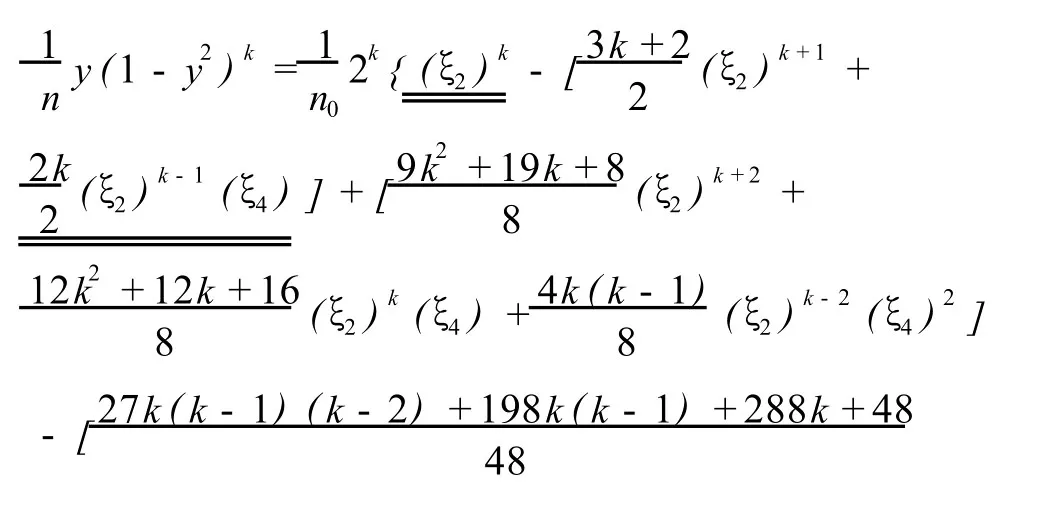

在文献[1,2]中,当 k≤2时,上式右端大括号中只有带下划线的项;当 k>2时,只考虑到了第一个下划线的项,而没有其他项,且只是考虑到了 k=4的项。
为方便编程计算,定义数组:

这里 J和L属于自然数集。把式 (13)代入式 (7),并利用式(14)可得

为便于计算机编程计算,同时使得对式 (13)的积分与式(14)数组的定义相符合,约定

在没有具体约定数组的数值时,其数值由式 (14)的定义求出。可见,如能确定 A(J,L),那么可由式(15)计算 E(k),然后再代入到式 (8)就得到了亚毫角秒理论精度的天文大气折射级数表达式。
3 基于位势地心距的级数展开
在大气物理学和海洋物理学的实际应用中,常采用位势高度而不用几何高度表示大气的高度和海洋的深度。一般情况下,位势高度 (z-r0)和几何高度 (r-r0)的关系是[10]:
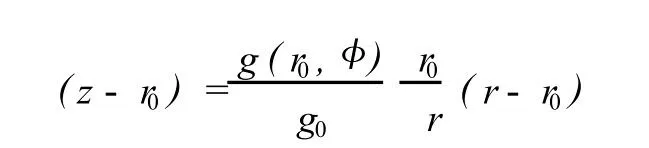
这里,g(r0,φ)是测站处的重力加速度,g0为常数。本文假设 g0=g(r0,φ),那么就有

对于大气折射理论研究,采用位势高度的优点在于可以不考虑压高公式中的重力加速度随高度和纬度的变化,只需知道测站重力加速度即可。以式(17)代替式(10)的第一式,按照上节推导过程可得基于位势地心距的数组(k)的表达式:

其中,数组A(J,L)仍按式(14)和(16)计算,但要以代替式 (9)第一式的ξ2。最后,以(k)代替式(8)的 E(k),就得到基于位势地心距的天文大气折射级数表达式。
4 结论与讨论
文献[1,2]给出的级数展开式只保留到角秒量级,但即使如此,也忽略了式 (13)中的第一中括号中的第一项。本文使得级数展开式可以取到任意阶次项,而文献[1,2]理论只是展开到了视天顶距正切的 9次方项。在文献[1,2]最终给出的公式中,并没有采用以视天顶距正切为引数形式的表达式,这在实际应用中很不方便,而本文最终给出的结果是以视天顶距正切为引数的级数表达式。同时把地面附近的位相折射指数作为未知数单独提出来,适应了光学观测技术在不同观测波长情况下的处理。
本文不但给出了基于几何地心距的蒙气差级数展开式,同时也给出了基于位势地心距的蒙气差级数展开式。计算数组 E(k)或A(J,L),需要一定的大气分布模型,随着大气探测资料和数值天气预报模型的完善,以及 GPS气象学的发展[11,12],可得到满足精度要求的大气分布模型。
1 OrlovB A.Refraction tables of the Pulkova observatory,4th Edition[M].Russian Academy of Science Press:Leningrad, Moscow,1956.
2 W illis J E.A determination of astronomical refraction from physical data[J].Transactions of the American Geophysical Union,1941,22(Part II):324-336.
3 GarfinkelB.An investigation in the theoryof astronomical refraction[J].Astronomical Journal,1944,50(8):169-179.
4 Garfinkel B.Astronomical refraction in a polytropic at mosphere[J].Astronomical Journal,1967,72(2):235-254.
5 Saastamoinen J.Contributions to the theory of atmospheric refraction,partI,astronomical refraction[J].Bulletin Géodésique,1972a,105:279-299.
6 Saastamoinen J.Introduction to practical computation of astronomical refraction[J].Bulletin Géodésique,1972b,106:383-397.
7 黄捷.电波大气折射误差修正[M].北京:国防工业出版社,1999.(Huang Jie.The radio-wave refractive error correct[M].Beijing:NationalDefense Industry Press,1999)
8 冒蔚,杨磊,铁琼仙.测定瞬时天文大气折射值和建立本地实测模型 [J].天文学报,2009,50(2):180-188. (MaoWei,YangLei and TieQiongxian.Atmospheric refraction and building a localobservationalmodel[J].ActaAstronomica Sinica,2009,50(2):180-188)
9 冒蔚,铁琼仙,杨磊.天文大气折射[M].昆明:云南科技出版社,2004.[Mao Wei,Tie Qiongxian and Yang Lei. Astronomical atmospheric refraction[M].Kunming:Yunnan Science and Technology Press,2004)
10 裴盛轩,等.大气物理学[M].北京:北京大学出版社, 2003.(Pei Shengxuan,et al.Atmospheric physics[M]. Beijing:BeijingUniversity Press,2003)
11 宫晓艳,等.大气掩星反演误差特性初步分析[J].地球物理学报,2007,50(4):1 017-1 029.(Gong Xiaoyan,et al.Inversion of atmospheric occultation preliminary analysis of error characteristic[J].Chinese Journal of Geophysics, 2007,50(4):1 017-1 029)
12 虞南华,朱文耀.GPS大气掩星技术在全球气候变化研究中的应用[J].地球物理学进展,2008,23(3):722-730.(Yu Nanhua and ZhuWenyao.Application of GPS radio occultation data in global climate change study[J].Progress in Geophysics,2008,23(3):722-730)
SERIES EXPANSI ON OF ASTRONOM ICAL ATMOSPHERIC REFRACTI ON
Zhang Hanwei,DingAnmin and LeiWei wei
(School of Surveyingamp;Land Infor m ation Engineering,Henan Polytechnic University,Jiaozuo 454003)
The correction ofAstronomicalAtmospheric Refraction(AAR)is one of the i mportant topics in astronomy and geodesy.On the basis of the literature 1 and 2,series expansion theory of AAR was restudied,a new series expansion was provided. The new expansion can expanded to the arbitrary order and times items,and reached the sub-milli-arc-second theoretical accuracy.In addition,the phase atmospheric refractive index near the ground had been extracted from the expansion,as a single unknown parameter,so,new expansion can be adapted to different observation wavelengths processing of optical technology.Finally,the new series expansion making tangent of visual zenith distance as a argument is given.Thiswork will completely replace the formula in AAR table of Pulkovo Observatory.Thismethod can also be applied to the theory of ray tracing.
AstronomicalAtmospheric Refraction(AAR);series expansion;at mospheric refractive index;sub-milliarc-second accuracy;formula for refraction table of Pulkova
1671-5942(2011)04-0060-04
2011-04-23
国家自然科学基金 (41040035);河南省科技创新人才杰出青年科学基金 (094100510023);河南省基础与前沿研究项目(082300460140)
张捍卫,男,1967年生,教授,博士后,博士生导师,主要从事空间大地测量学教学和研究工作.E-mail:zhanwei800@163.com
P172
A
