不同数据预处理方法对北斗卫星精密定轨精度的影响*
2011-11-23郝金明贾小林
周 巍 郝金明 贾小林
(1)解放军信息工程大学测绘学院,郑州 450052 2)中国人民解放军63883部队,洛阳 471003 3)西安测绘研究所,西安710054)
不同数据预处理方法对北斗卫星精密定轨精度的影响*
周 巍1,2)郝金明1)贾小林3)
(1)解放军信息工程大学测绘学院,郑州 450052 2)中国人民解放军63883部队,洛阳 471003 3)西安测绘研究所,西安710054)
提出综合利用高次差法和多项式拟合法对COMPASS-MEO卫星进行周跳探测的原理及实现方法,并采用COMPASS监测站实测数据使用不同的数据预处理策略对COMPASS-MEO卫星进行精密定轨试验。结果表明,根据实测数据情况,合理选择周跳探测方法和预处理策略,可以改善定轨精度。
COMPASS;周跳;φLC-PLC组合;多项式拟合;定轨
1 引言
卫星导航系统将导航卫星作为动态已知点,实现精密定轨是首先需要解决的问题,而观测数据质量是影响卫星定轨精度的重要因素之一。对载波相位观测数据而言,未被检测出的周跳将被位置参数的改正数所吸收,从而导致参数估计的有偏。长期以来学者们对GPS周跳探测与修复问题做了深入的研究,对COMPASS系统具有重要的借鉴作用。与GPS相比,COMPASS提供更多类型的观测数据,对于各类数据以前并没有使用的经验,传统GPS数据预处理中周跳探测方法是否适用于COMPASS,是否能够改善定轨精度,都有待进一步研究。
本文提出了综合利用高次差法和多项式拟合法探测周跳的方法,并利用COMPASS监测站实测数据,分析了不同周跳探测方法和数据预处理方案对COMPASS-MEO卫星定轨结果的影响。
2 周跳探测原理
2.1 利用φLC-PLC组合探测周跳
周跳探测原理基于粗差理论,构造能够精确反映周跳变化的检验序列,使周跳在该检验序列中以粗差的形式体现,进而确定周跳的位置和大小。
构造双频消电离层组合为:
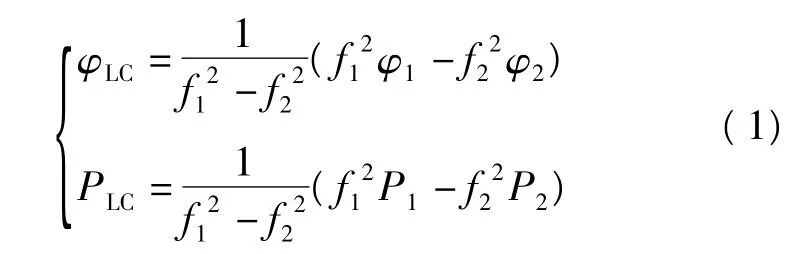
φLC-PLC组合消除了几何距离、电离层、对流层、钟差的影响,对该组合相邻历元间求差,若无周跳发生,残差应该在0值上下随机波动,而周跳会以粗差的形式突显于该检验序列中。由于φLC-PLC组合放大了观测噪声(约为P1噪声的3倍[1]),直接影响周跳探测的灵敏度,实验发现该方法对10周以内的周跳不敏感,且利用φLC-PLC组合探测周跳只能反映周跳位置,并不能分离出某一个频率上的周跳幅值。
2.2 综合利用高次差法和多项式拟合法探测周跳
多项式拟合法根据m个无周跳的载波相位观测值拟合一个n阶多项式,根据多项式预估下一个观测值并与实测值比较,从而发现周跳并修正整周计数[2]。
其数学模型为:
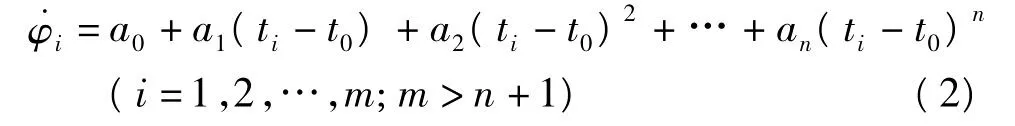

如图1和表1所示,对于观测质量较好的大采样率数据而言,该方法对周跳的探测十分敏感,且周跳估值与预设值非常接近。
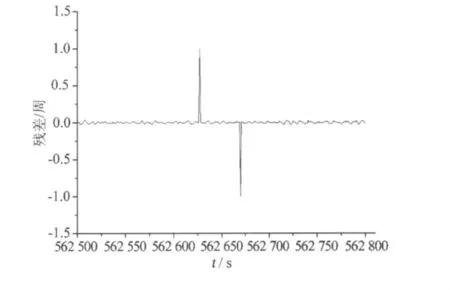
图1 多项式拟合法探测周跳Fig.1 Cycle slip detection by polynomial fitting
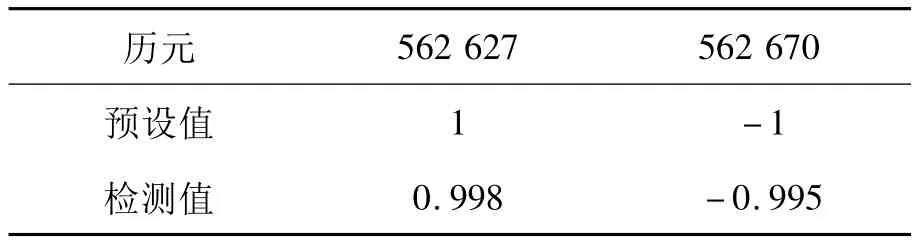
表1 多项式拟合法周跳检测结果(单位:周)Tab.1 Results of cycle slip detection by polynomial fitting (unit:cycle)
采用多项式拟合法探测周跳存在以下问题:每弧段启动第一个窗口(拟合窗宽度m)拟合系数并对第m+1历元进行外推时,若前m个历元就已发生周跳,会引起之后一系列误报。而通过对大量实测数据分析发现,这种现象比较常见,是必须要解决的问题。
采用 Remondi提出利用差分法进行周跳探测[4]。采用原始观测数据或者其线性组合值历元间求差,可以消除一些误差,如接收机钟差、卫星钟差、大气折射延迟等,当求至5次差时,如果没有周跳发生,该高次差序列呈现偶然误差特性,而周跳则会破坏这种规律性且幅值被放大,这类似一个高通滤波器,既阻尼低频又消除其常数部分,高频部分(如周跳)则被放大,根据该特性可以确定周跳发生的位置[5]。
联合使用高次差法和多项式拟合法探测周跳,在多项式拟合法启动第一个窗口内,首先对该m个数据使用高次差法进行探测,如果发生周跳,确定其发生时刻,从该历元起重新开窗,直到有m个“干净”的观测数据起再启动多项式拟合法探测周跳。
3 基于Hatch滤波的COMPASS双频载波相位平滑伪距
鉴于载波相位测量精度高,能够精确反映伪距的变化,且多路径误差影响大约是测码伪距观测值的1/10等[6]原因,利用载波相位信息辅助码伪距测量,以获得比单独采用码伪距测量更高的精度[7],基本公式为:

式(3)中包含历元ti的电离层折射误差相对于前i个历元平均值的变化。当历元间的电离层折射发生变化时,伪距平滑值中包含2倍电离层延迟变化影响,当电离层延迟发生突然抖动时,单频伪距相位平滑的结果中会包含较大的偏差[8]。因此,单频伪距进行多历元数据的平滑处理时,如果所采用弧段的长度不适当,可能会发生单频伪距相位平滑值的离散情况。
通过对大量实测数据的分析,本文选取的B1、B3频率窄相关类型伪距和载波相位用于定轨运算。如式(1)构造双频电离层组合,将式(3)转化为:采用Hatch滤波方法[9],双频相位平滑伪距逐历元递推计算公式表示为:

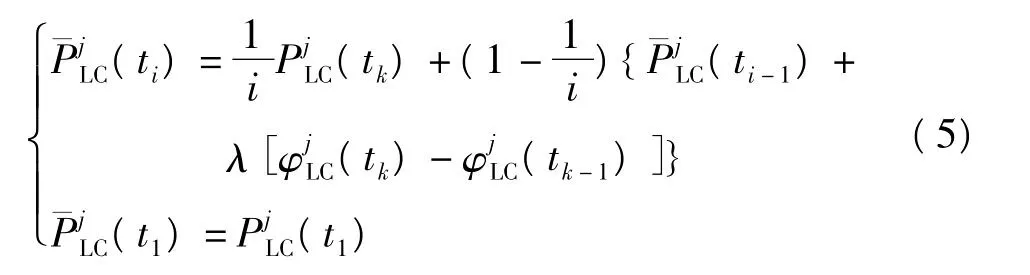
选取2008年9月5日COMPASS-MEO临潼站观测数据,如(5)式获得B1、B3双频相位平滑伪距值,与B1频率窄相关伪距对比,分析基于Hatch滤波的COMPASS-MEO双频相位平滑伪距值对精度的改善,图2、图3分别为伪距和载波相位平滑伪距拟合噪声残差图,计算相应RMS值统计如表2。
结果表明,B1频率窄相关伪距观测噪声约为0.200 m,载波相位平滑伪距后为毫米级,大大降低了噪声水平。故采用双频载波相位平滑伪距数据进行定轨可以获得更高的精度。
4 定轨结果分析
选取2008年3月4、5、6日,上海站、长春站、临潼站、昆明站、乌鲁木齐站、南极站观测数据,对COMPASS-MEO卫星进行动力学法定轨,比较不同周跳探测方法、不同预处理策略对定轨结果的影响。

图2 伪距拟合残差图Fig.2 Residual of pseudorange polynomial fitting

图3 载波相位平滑伪距拟合残差图Fig.3 Residual of pseudorange polynomial fitting of carrrier phase
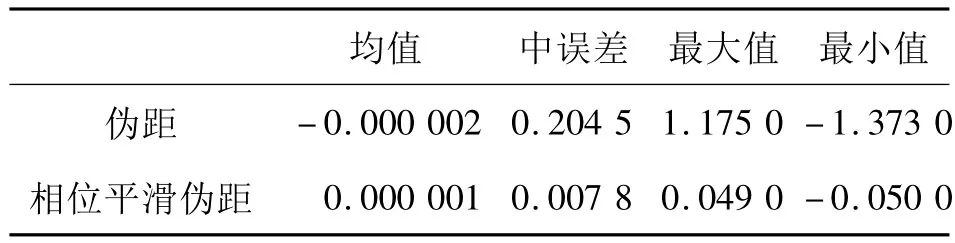
表2 临潼站数据拟合噪声统计表(单位:m)Tab.2 Polynomial fitting noise of Lintong station(unit:m)
4.1 数据预处理
以2008年3月4临潼站相位观测数据为例,分别使用方案2和方案3对观测数据进行预处理,比较其结果。
如图4所示,该时间段内相位数据发生了较大的周跳,两种方法都能够将其成功探测。多项式拟合法可以确定某一频率发生周跳的位置和大小,并将其成功修复;而无论哪一个频率相位数据发生周跳,组合历元间求差都会以粗差形式显现,但由于该段载波相位数据频繁发生周跳,按照方案2的数据分段思想,会使得段内数据量较少,可能会影响定轨结果。

图4 周跳探测结果Fig.4 Results of cycle slip detection
4.2 精密定轨
采用3种不同策略对观测数据进行预处理后进行精密定轨。
方案1:采用B1频率窄相关伪距观测量定轨;
方案2:利用φLC-PLC对B1、B3频率组合进行周跳探测,标记周跳发生的位置将数据分段,段内相位平滑伪距后定轨;
方案3:综合利用高次差法和多项式拟合法分别对B1、B3频率相位数据进行周跳探测和修复,使用修复后的全弧段相位平滑伪距数据定轨(图5)。
采用定轨残差的RMS作为评定精度的指标,统计结果如图6和表3所示。

图5 数据处理流程图Fig.5 Flow chart of data processing

图6 各站定轨残差RMS统计Fig.6 Residual RMS statistics graph of orbit determination at each station
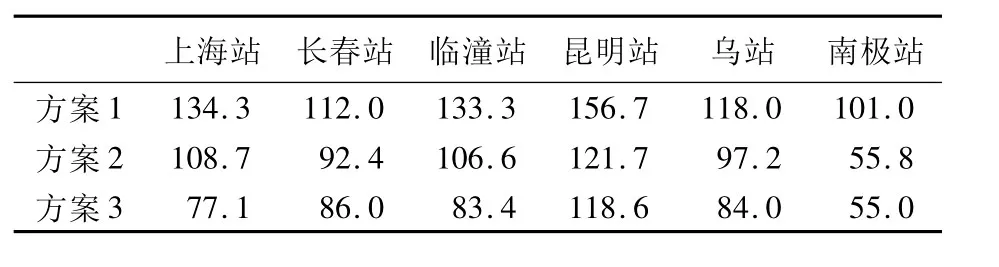
表3 各站定轨残差RMS统计(单位:m)Tab.3 Residual RMS statistics of orbit determination at each station(unit:m)
结果表明:使用相位平滑伪踞数据可以获得比使用伪踞观测值更高的定轨精度;对于幅值较大的周跳,方案2、3中的两种方法均能够成功探测,此时方案2、3定轨精度基本相当,如表2中长春站、昆明站等;对于频繁发生周跳的观测数据(如表2中上海站、临潼站),联合使用高次差法和多项式拟合法进行周跳的探测并将其修复,能够改善定轨精度。对于较频繁发生周跳的载波相位数据,采用修复周跳全弧段平滑的策略较分段平滑能够获得更高的定轨精度,分析其原因,对于式(4)应用误差传播定律得到双频相位平滑伪距值方差为:

另外,对于渐进稳定的Hatch滤波器,当滤波时间充分长后,其最优滤波值将渐进地不依赖于滤波初值的选取[10],而当数据量较小时,初值中伪距的因素会对平滑伪距值产生影响。
5 结论
本文将φLC-PLC组合法、综合利用高次差法和多项式拟合法应用于COMPASS-MEO卫星载波相位数据周跳探测,利用精密定轨结果对比分析不同周跳探测方法和预处理策略对精度的影响,在COMPASS数据处理过程中,应根据实际观测数据情况,综合考虑周跳修复难度、精度要求、运算效率等因素,合理选择周跳处理方法及预处理策略。
1 常志巧.利用非差观测量确定GPS卫星导航轨道的方法研究[D].解放军信息工程大学,2006.(Chang Zhiqiao.A study of the orbit determination of GPS satellite using zerodifference observation[D].Information Engineering University,2006)
2 魏子卿,葛茂荣.GPS相对定位的数学模型[M].北京:测绘出版社,1998.(Wei Ziqing and Ge Maorong.The mathematical model of GPS relative positioning[M].Beijing:Publishing House of Surveying and Mapping,1998)
3 罗峰,姚宜斌,宋伟伟.综合利用多项式拟合和载波相位变化率探测单频GPS周跳[J].全球定位系统,2007,32(5):9-13.(Luo Feng,Yao Yibin and Song Weiwei.Detection for cycle slips using polynomial fitting and carrier phase rate method[J].GNSS World of China,2007,32 (5):9-13)
4 刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2006.(Liu Jiyu.GPS satellite navigation and positioning principles and methods of navigation[M].Beijing:Science Press,2006)
5 严新生,王一强,白征东.联合使用高次差法和 T urboEdit法自动探测、修复周跳[J].测绘通报,2007,53 (9):23-26.(Yan Xinsheng,Wang Yiqiang and Bai Zhengdong.Automatically detect and repair cycle slips using all iance of high difference and turboedit[J].Bulletin of Surveying and Mapping,2007,53(9):23-26)
6 Misra Pratap and Enge Per.Global positioning system:signals,measurements,and performance[M].Lincoln,Mass:Ganga-Jamuna Press,2001.
7 唐卫明,刘智敏.GPS载波相位平滑伪距精度分析与应用探讨[J].测绘信息与工程,2005,30(3):37-39.(Tang Weiming and Liu Zhimin.Precision evaluating and applications of GPS code pseudorange smoothing algorithm based on carrier observables[J].Journal of Geomatics,2005,30(3):37-39)
8 范士杰.GPS精密单点定位的算法实现与精度分析[D].武汉大学,2004.(Fan Shijie.The algorithm and accuracy analysis of GPS precise point positioning[D].Wu Han University,2004)
9 Hatch R.The synergism of GPS code and carrier measurements[A].In:Proceedings of the Third International Geodetic Symposium on Satellite Doppler Positioning[C].Las Cruces,New Mexico.,USA,1982,1 213-1 232.
10 付梦印,邓印红,张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003.(Fu Mengyin,Deng Yinhong and Zhang Jiwei.Dynamic Kalman filtering theory and its application in navigation system[M].Beijing:Science Press,2003)
INFLUENCE ON ACCURACY OF COMPASS ORBIT PRECISION DETERMINATION WITH DIFFERENT DATA PREPROCESSING METHODS
Zhou Wei1,2),Hao Jinming1)and Jia Xiaolin3)
1)Institute of Surveying and Mapping,Information Engineering University,Zhengzhou 450052 2)63880 Troops,Luoyang 471003 3)Xi’an Research Institute of Surveying and Mapping,Xi’an710054
How to detect the cycle slip is always the key to data preprocessing for satellite orbit determination.The method of LC-PC combination,Multi-difference combined Polynomial fitting for cycle slip detecting is analyzed,and then the test of orbit precision determination using COMPASS observations is made.It shows that,as for the observations of COMPASS receiver,the accuracy of orbit determination will be improved by choosing the methods of cycle slip detecting and data preprocessing rationally.
COMPASS;cycle slip;φLC-PLCcombination;polynomial fitting;orbit determination
1671-5942(2011)06-0084-05
2011-06-07
国家自然科学基金(40604003)
周巍,女,1981年生,博士研究生,主要从事GNSS理论研究与数据处理.E-mail:zhouwei_0611@163.com
P227
A
