移动格林基函数样条二维插值算法研究*

邓兴升 汤仲安

(1)长沙理工大学测绘工程系，长沙 410004 2)湖南省测绘科技研究所，长沙410004)

移动格林基函数样条二维插值算法研究*

邓兴升1)汤仲安2)

(1)长沙理工大学测绘工程系，长沙 410004 2)湖南省测绘科技研究所，长沙410004)

针对用于插值的已知点较多时，插值计算需要解算大规模矩阵、计算耗时长甚至无法解算的问题，引入移动曲面的思想，取插值点周边最邻近k个已知点进行格林基函数二维样条移动插值，实例计算结果表示，该方法的插值精度高于Shepard插值法与多项式拟合法的精度。插值范围大及测点数量众多时，该方法仍可用，无需数据分区与光滑接边，与整体插值相比可大大降低计算时间。

移动格林基函数;二维样条;插值算法;整体插值;移动插值

1 引言

在大地测量领域，需要由离散观测的型值点来构造自由曲面。由于区域广、范围大，与空间位置相关的属性难以用一个数学函数来表达，因而需先建立规则的格网，然后在格网的基础上进行插值计算。目前国内外常采用的插值方法有：多项式拟合、Shepard反距离加权、Hardy多面函数、Kriging、人工神经网络［1］、最小曲率样条插值［2］等。

多项式拟合存在以下不足：1)复杂曲面难以由有限参数的多项式精确拟合;2)构造的曲面容易产生多余摆动且难以发现;3)多项式插值存在“龙格现象”，曲面边缘会产生畸变;4)大面积曲面必须分区拟合，接边时容易产生错位;5)多项式次数及参数个数需要依赖经验调整或多次试算;6)当曲面复杂时，必须用高次多项式，而高次多项式振动大、不稳定，用它进行预测效果很差。Shepard插值原理是反距离加权插值，即将插值函数定义为各型值点的加权平均值，权函数定义为与距离成反比或采用分段函数，反距离加权插值会引起曲面畸形及错开的现象［3］。Hardy多面函数的光滑因子需人工主观确定，且对拟合结果影响显著，这种方法有严重缺陷甚至错误，已被否定［4］。

最小曲率样条插值认为插值点形成的曲面应满足整体曲率最小的原则，由于整体曲率最小在理论上很合理，生成的曲面具有光滑性，因而成为主流插值方法。然而该方法生成的曲面会在已知控制点之间产生多余的摆动，Schweikert［5］提出张力样条，以克服多余摆动，Cline［6］实现了张力样条。David［7］在最小曲率准则的基础上提出了格林基函数插值法，在构造曲面方式上进步较大，但当型值点的分布极度不均衡时，插值结果欠稳定，且同样存在曲面多余摆动的问题［8，9］，文献［8］采用张力样条以克服该方法的多余摆动，张力样条得到广泛认同和应用［9-11］。在已知点相对较密时，张力样条会提高插值精度，但已知点分布不均匀及相对较稀时插值结果仍欠稳定，张力样条构造曲线在某些情形下呈波浪形，产生抖动现象，致使曲线失真［12］。

在大范围插值问题中，会碰到大量非规则分布的离散点，如果要解算大规模矩阵，计算量巨大，计算速度慢，随着型值点的增加计算非常缓慢甚至无法进行。因此本文引入移动曲面的思想，以待插值点周边最邻近的若干点实施格林基函数二维样条插值，从而减少计算时间;采用插值点周围最邻近的若干点进行移动插值，改变了型值点分布的均衡性，有利于提高插值结果的稳定性。

2 移动格林基函数样条二维插值算法

曲面s(x)可表达为：

式中，x为已知点的位置参数;g(x，xj)为格林函数; xj为第个插值点的位置;wj是与xj相关联的未知权值;T(x)为倾向参数，一般为常数，它代表不能由格林函数表达的那部分地区性倾向参数，在对曲面s(x)建模之前，首先要把T(x)从数据中移去，建模之后再恢复T(x)，从而不考虑对T(x)的建模。式(1)中权值wj是满足

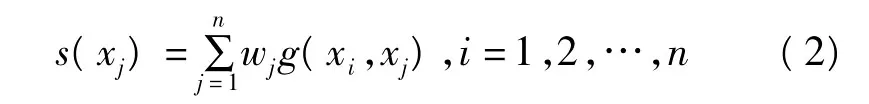
的解。其中格林函数g(xi，xj)表达式为

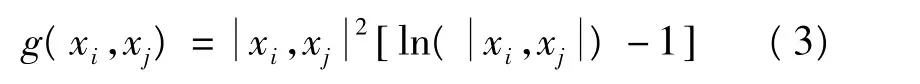
设某测区共有n个已知点，当n=5 000时，在PC机(CPU：2G Hz，内存1G)上进行一次5 000阶的矩阵求逆运算需要4～5分钟，如果格网达10 000个结点以上，则计算耗时漫长。移动插值认为，插值只是局部行为，待插值点p0的值只与其周边最邻近的若干个点相关。本文以待插值点为圆心，变动半径使落入圆中的已知点数等于阈值k。移动格林基函数样条二维插值算法如下：

1)设测区共有n个已知点，插值点为 p0(x0，y0)，参与p0点插值计算的最邻近点数为k，较小的k值(如k＜30)会影响计算精度;增加k值能提高插值精度，但达到某一阈值时(通常小于100)会出现饱和现象，即插值精度不再提高。根据p0(x0，y0)与已知点(xi，yi)计算其距离r0：

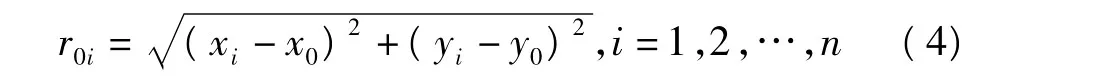
将r0i按归并排序算法从小到大排序，取得距离最小的前k(k≤n)个已知点的序号及坐标(xj，yj，zj)，j=1，2，…，k。

2)设前k个已知点构成的矩阵为X=［x1x2…xk］T，Y=［y1y2… yk］T，Z=［z1z2… zk］T。设k×k阶方阵为

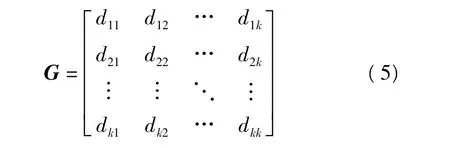
式中

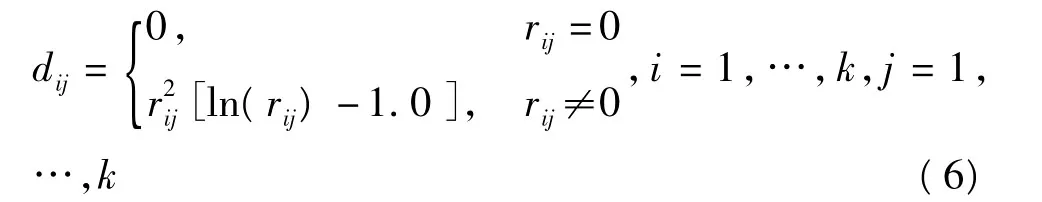
3)计算插值点p0(x0，y0)的1×k阶矩阵Gp：

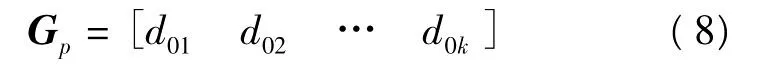
式中d01，d02，…，d0k按式(6)计算，式(6)中的r0j即为p0至k个已知点的距离。采用第1)步计算的相应结果，则所求p0点插值zp为：

4)重复1)～3)步，依次求出其他点pi(xi，yi)的插值zpi。

从以上步骤可知，移动格林基函数样条二维插值算法有如下特点：算法简洁;算法基于点与点之间的距离及其衍生函数，而与方向无关;已知点数量任意多时，插值只在最邻近的k个点中进行，因而仍可行;无需对数据分区与光滑接边。

3 实例分析

3.1 插值精度比较

以二元三次多项式十参数法、Shepard插值法作为对比方法。已知曲面为：

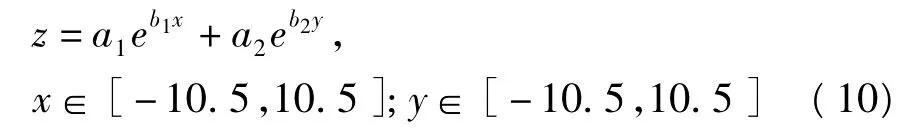
其中a1=0.4，b1=0.3，a2=-0.8，b2=0.2。实验中变更这些参数，结果类似。由式(10)产生若干已知点和测试点，均无误差，因而插值结果只与不同方法自身有关。在(x，y)的定义域内以2.9为间隔取64点作为已知点，以间隔2.13取100点作为测试点。已知点构造的曲面如图1所示。

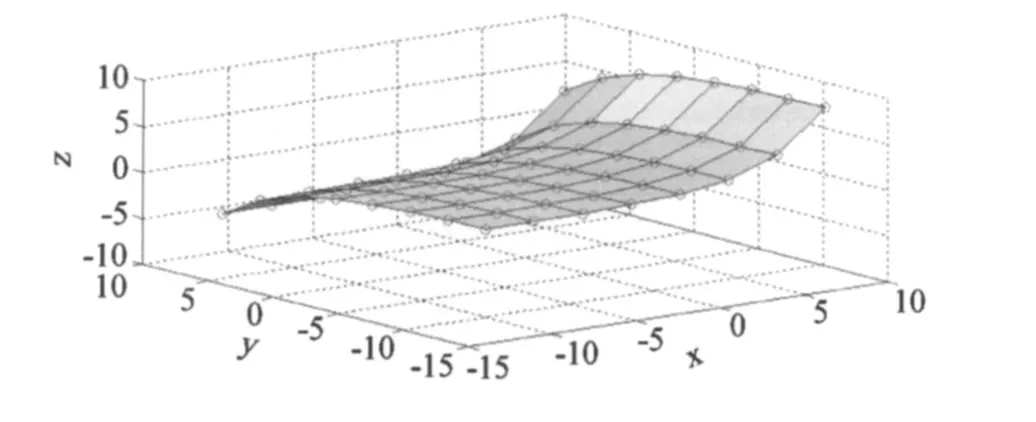
图1 试验的已知曲面Fig.1 Experimental surface(8×8 grid)

二元三次多项式十参数法模型如下：

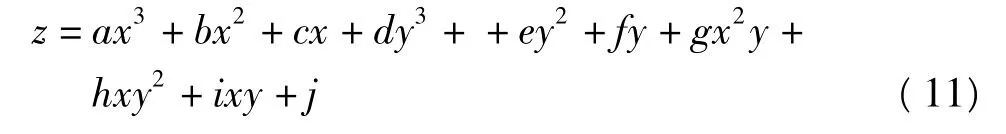
其中a～j为模型参数;x、y为点的坐标;z为与x、y对应的属性值。根据最小二乘法计算出模型参数，再计算测试点，并与真值比较，其差异如图2所示。

由图2可知，二元三次多项式拟合会出现规则的变形，曲面中间出现规则的“鞍状上凸”，边缘出现了“翘曲”，误差最大值为 0.354，最小值为-0.427。Shepard插值采用了以距离倒数为权值的加权插值，测试点插值结果与真值比较，其差异如图3所示。采用本文方法由64个已知点插值得到的曲面与真实曲面比较，其差异曲面如图4所示。

由图3可知，Shepard反距离加权插值曲面与真实曲面相差较大，误差最大值为3.183，最小值为-2.727。由图4可知，本文方法插值曲面与真实曲面在区域中央误差接近为0，没有“上凸”或“下凹”现象;但在曲面内侧边缘有畸变，误差最大值为0.326，最小值为-0.201。

为了考察已知点数量增多的情况下各种方法的插值精度，将取点间隔适当缩小，在(x，y)的定义域内以间隔1.8取得144点;以间隔1.5取得225点;以间隔1.3取得289点，由不同方法分别计算100个测试点的插值精度。为了在同等条件下进行比较，3种方法都采用了全部已知点进行插值，表1为3种方法插值中误差的比较结果。

图2 二元三次多项式拟合误差曲面Fig.2 Error surface of binary cubic polynomial fitting

图3 Shepard插值误差曲面Fig.3 Error surface of Shepard’s interpolation

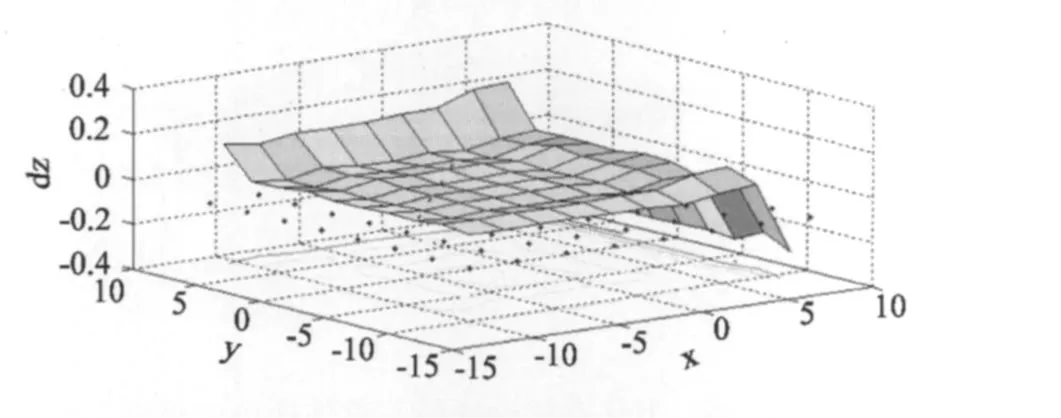
图4 格林基函数样条插值误差曲面Fig.4 Error surface of spline interpolation based on Green’s function

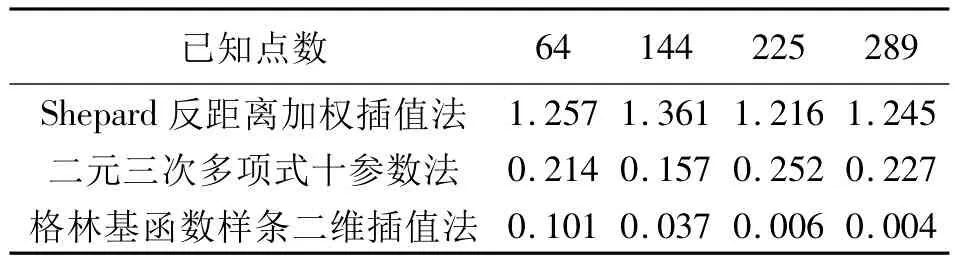
表1 不同已知点数量的情况下3种方法的中误差比较Tab.1 Comparison among the mean square errors with three methods with different number of data points

从表1可知，Shepard方法在本例中的插值中误差较大;格林基函数样条二维插值法在本例中的插值精度最高;随着已知点数量的增加，Shepard插值法和二元三次多项式十参数法精度没有改善，甚至降低;而本文方法插值精度随着已知点数量的增加不断提高。

3.2 计算时间比较

已对某曲面均匀观测了3 564个测点，欲根据观测数据生成60×60的正方形格网，插值方法采用格林基函数二维样条插值，本例对采用全部3 564点整体插值与采用最邻近100点移动插值的计算时间进行比较，结果见表2。算法采用C++语言编程实现，测试计算机的配置为CPU：2G Hz，内存1G。

表2 整体插值与移动插值的计算时间比较Tab.2 Comparison between the computation time as k= 3 564 and k=100

由表2可知，采用最邻近100点移动插值可以大大缩短计算时间。为了考查采用最邻近100点插值时的精度有没有受到影响，因该曲面模型未知，插值结果无法与真值比较，我们将其与整体插值的格网进行比较，两格网之间的差异如图5所示，差异最大值为2.7 mm，最小值为-3.3 mm，中误差仅为0.4 mm，表明插值结果非常接近。

图5 最邻近100点移动插值与整体插值的格网差异Fig.5 Interpolated Grids’differences between the results from moving interpolation and global interpolation

试验进一步增加k值，当k到达阈值时即出现饱和现象，即插值精度不再提高，此时采用最邻近k点插值与采用全部点插值的结果相同，因此没有必要采用全部点插值，从而在保障精度的同时又节省计算时间。

4 结论

针对插值过程中求解大规模矩阵困难的问题，引入移动曲面的思想，以待插值点周围最邻近的若干点进行移动格林基函数二维样条插值，算法简洁，易于编程使用。实例中该方法插值精度高于二元三次多项式拟合和Shepard反距离加权插值的精度，且随着已知点数量的增加能不断地提高插值精度。已知点数量任意多时，整体插值难以进行，移动插值只在最邻近的k点中进行因而仍可实施，插值精度与整体插值相同，并且无需对数据分区与光滑接边，减小过程复杂性，极大地缩短计算时间。

1 尤淑撑，严泰来.基于人工神经网络面插值的方法研究［J］.测绘学报，2000，29(1)：30-34.(You Shucheng and Yan Tailai.A study on artificial neural network based on surface interpolation［J］.Acta Geodaetica et Cartograpphica Sinica，2000，29(1)：30-34)

2 Briggs I C.Machine contouring using minimum curvature［J］.Geophysics，1974，39(1)：39-48.

3 邓兴升，郭云开，花向红.似大地水准面格网双二次多项式插值方法［J］.测绘学报，2009，38(1)：35-40.(Deng Xingsheng，Guo Yunkai and Hua Xianghong.Quasigeoid grid network biquadratic interpolation method［J］.Acta Geodaetica et Cartograpphica Sinica，2009，38(1)：35-40)

4 Jekeli C.Hardy’s multiquadric-biharmonic method for gravity field predictions［J］.Computers＆Mathematical Applications，1994，28(7)：43-46.

5 Schweikert D G.An interpolating curve using a spline intension［J］.Jour Math Physics，1966，45(2)：312-317.

6 Cline A.Scalar and planar-value curve fitting using splines under tension［J］.Comm ACM.，1974，(17)：218-223.

7 Sandwell D T.Biharmonic spline interpolation of GEOS-3 and SEASAT altimeter data［J］.Geophys Res Lett.，1987，14(2)：139-142.

8 Wessel P and Bercovici D.Interpolation with splines in Tension：A Green’s function approach［J］.Mathematical Geology，1998，30(1)：77-93.

9 Smith W H F and Wessel P.Gridding with continuous curvature splines in tension［J］.Geophysics，1990，55(3)：293 -305.

10 Mitásová H and Hofierka J.Interpolation by regularized spline with tension：II.Application to terrain modeling and surface geometry analysis［J］.Mathematical Geology，1993，25(6)：657-669.

11 Mitásová H and Mitás L.Interpolation by regularized spline with tension：I.Theory and implementation［J］.Mathematical Geology，1993，25(6)：641-655.

12 邓曙光，李婉.曲线光滑的张力样条插值法VC实现［J］.工程地球物理学报，2005，2(5)：387-390.(Deng Shuguang and Li Wan.Realization of smoothing curve with tension spline interpolation under visual C++［J］.Chinese Journal of Engineering Geophysics，2005，2(5)：387 -390)

STUDY ON TWO-DIMENSIONAL SPLINE INTERPOLATION BASED ON MOVING GREEN FUNCTION

Deng Xingsheng1)and Tang Zhongan2)

(1)Department of Surveying Engineering，Changsha University of Science＆Technology，Changsha 410004 2)Hunan Research Institute of Surveying and Mapping，Changsha 410004)

When the data coverage is dense，some algorithms need to solve large size matrix，thus the computation time is proportional approximately to the cube of the number of data constraints，it makes the process very slow.Focusing on this problem，the moving curvature is introduced in interpolation.Only the nearest data points are chosen for interpolating by two-dimensional spline based on the moving Green’s function.The examples show that the interpolation accuracy of the proposed method is higher than that of two other methods.No matter how many data points there are，this method can be implemented fast.It is not necessary to split the data into subsets which can be modeled individually，or to blend the subsets together into a final model.Comparing with the global solution，this algorithm can greatly reduce the computation time.

moving Green’s function;two-dimensional spline;interpolation algorithm;global interpolation;moving interpolation

1671-5942(2011)06-0069-04

2011-05-06

湖南省自然科学基金(10JJ3090)

邓兴升，男，1971年生，高级工程师，博士，主要从事大地测量数据处理研究.E-mail：whudxs@163.com

P207

A