基于矩阵列变换的标准正交基求法

陈云坤

(贵州师范大学数学与计算机科学学院,贵阳 550001)

基于矩阵列变换的标准正交基求法

陈云坤

(贵州师范大学数学与计算机科学学院,贵阳 550001)

给出了将Rn的一个基化为标准正交基的新方法.

列初等变换;三角矩阵;标准正交基

1 引 言

文[1-3]给出了用矩阵的合同变换求标准正交基的方法——合同变换正交化法.本文给出一种改进的求标准基的方法——顺序对角线正交化法.此方法简便易行.最后证明了在R3上将一个基化为正交基,与顺序对角线正交化法和Schmidt正交化法所得结果是一致的.

2 顺序对角线正交化法

定义1 设A=(aij)为n阶方阵.若存在可逆矩阵Pi,i=1,…,n-1,使得

其中Ak=(a(k)ij)是n-k阶方阵,a(0)11=a11,则称矩阵A可顺序对角化为下三角形矩阵.

定理2 设A=(aij)为n阶正定矩阵,则存在第三种初等矩阵之积P,使得

且对A施行合同变换后得

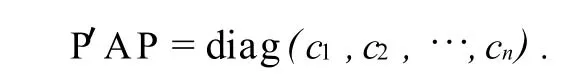
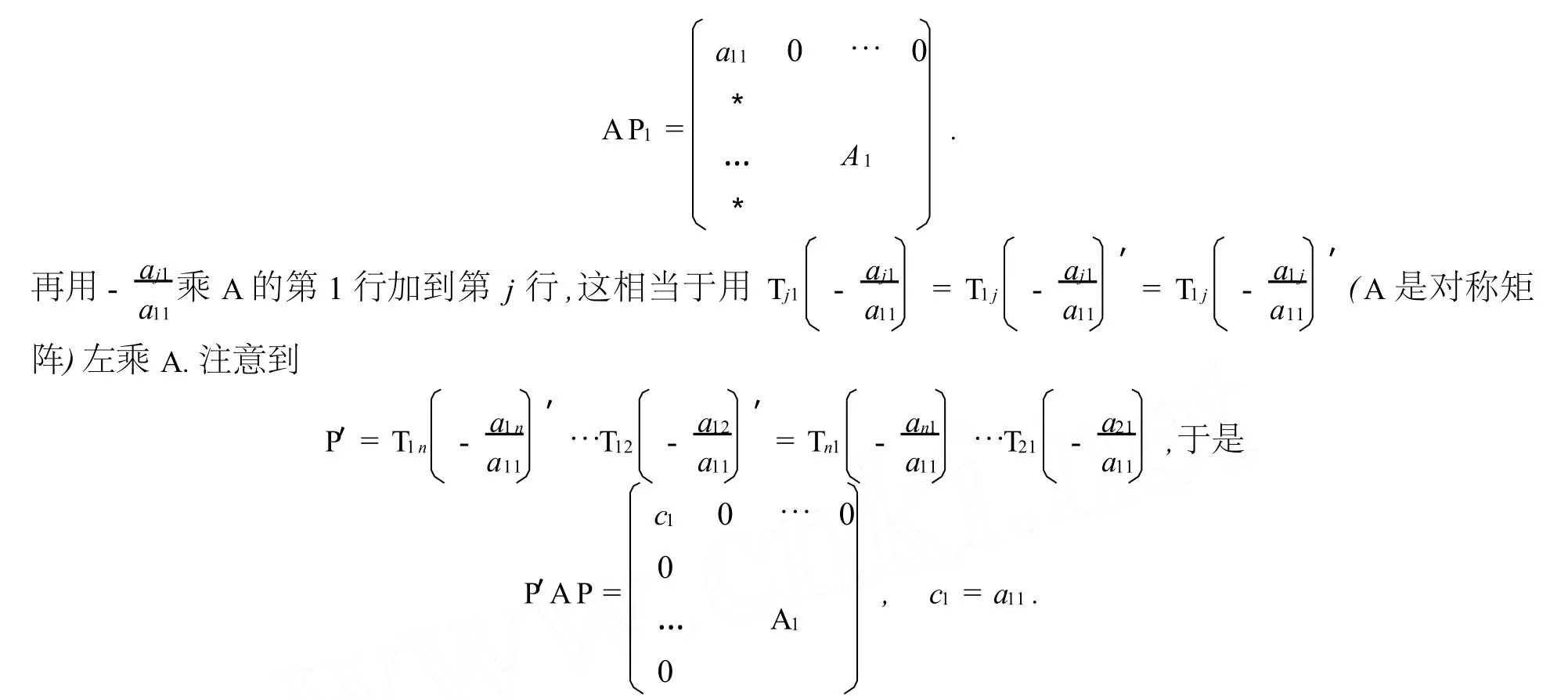
由A是正定矩阵可知,P′AP是对称矩阵,从而A1是n-1阶对称矩阵.设A1的k阶顺序主子式为|A1(k)|,则P′AP的k+1阶顺序主子式为

由正定矩阵的性质知,P′AP也是正定矩阵,于是P′AP的一切顺序主子式大于零,从而a11|A1(k)|＞0.由A是正定矩阵可知,a11＞0,从而|A1(k)|＞0.因此,A1的一切顺序主子式大于零,故A1是正定矩阵.

对A1仍可重复上述步骤,…,对上述步骤重复n-1次后便终止,这时,易知存在第三种初等矩阵之积Pi,i=1,…,n-1,使得

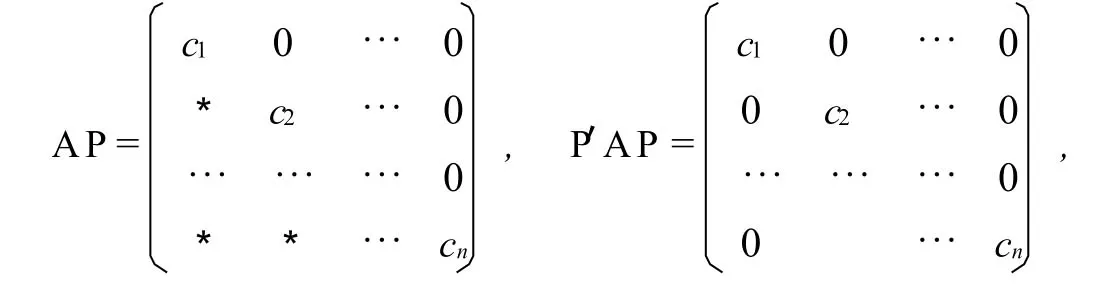
其中P=P1…Pn-1.

注1 由定理2的证明过程可得任意正定矩阵可顺序对角化为下三角形矩阵.我们把定理2中,将正定矩阵A初等变换为AP的过程称为对矩阵A施行顺序对角化化为下三角形矩阵.

新的正交化方法的原理 设αi=(a1i,…,ani)′,i=1,…,n是Rn的一个基,以αi为列向量构成矩阵A=(aij),则A′A是正定矩阵.由定理2知存在第三种初等矩阵之积P,使得A′PA和P′A′PA为下三角矩阵.由|P′A′AP|=c1c2…cn及A′A,P是可逆矩阵可得ci≠0.令,则

由上所述,我们得到将Rn的一个基α1,α2,…,αn化为标准正交基的一种新方法.

新的正交化法的具体的步骤:

(i)求A′A,其中A=(α1,α2,…,αn);

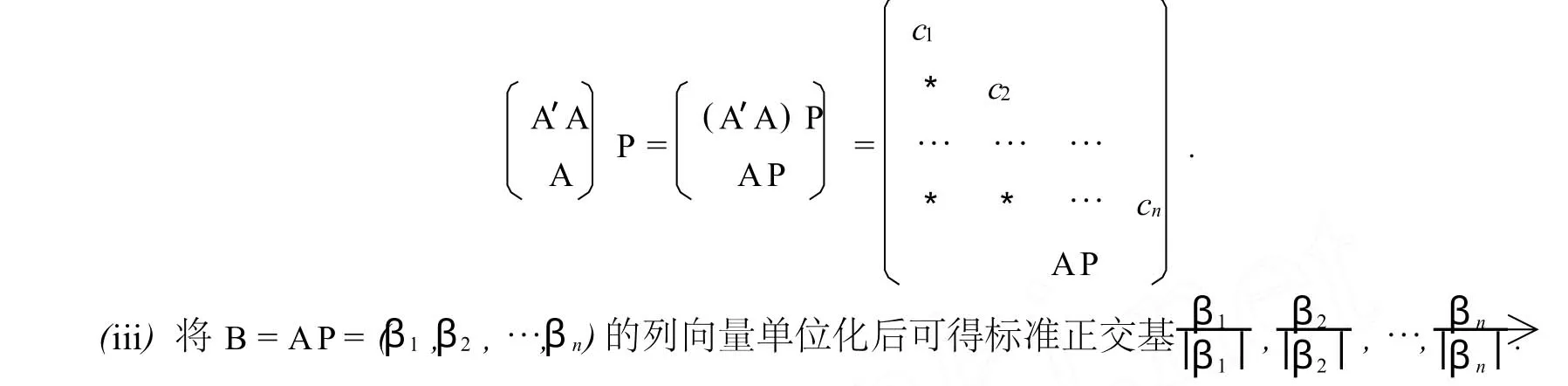
上述方法,我们将其称为顺序对角线正交化法.

注2 若将(ii)替换为

则顺序对角线正交化法变为合同变换正交化法.

3 顺序对角线正交化法的例子

例[4]在R3中将基

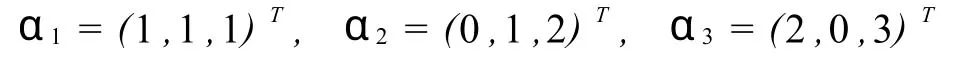
化为的标准正交基.

解 实施顺序对角线正交化法.

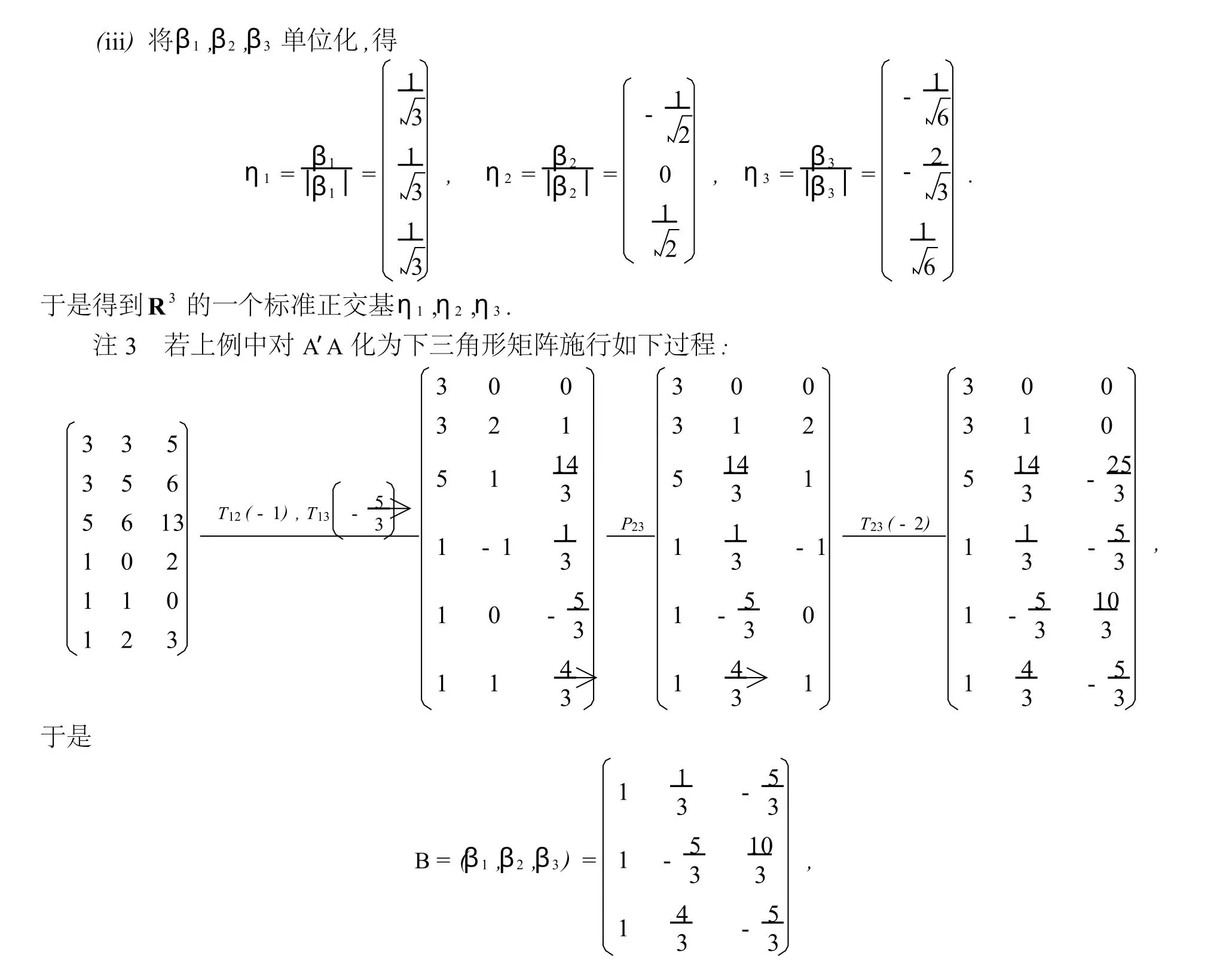
从而〈β2,β3〉=-,因此β1,β2,β3不是R3的一个正交基.这说明当把A′A化为下三角形矩阵时,采用的是非顺序对角化过程,则对A施行相同的列初等变换所得B=AP的列向量不一定是R3的一个正交基.

注4 若对上例利用Schmidt正交化法其结果(见[4,P497,例5])与上述方法的结果完全一致.事实上,我们有以下结果:

注意到β1,β2,β3是矩阵A利用Schmidt正交化法所得正交基,从而

注5 定理3表明对α1,α2,α3施行正交化采用顺序对角线正交化法和Schmidt正交化法所得结果是一致的.

[1] 李宗胜.标准正交基的一种求法[J].数学通报,1991,30(3)：21-25.

[2] 王桂兰.用矩阵的合同变换法求标准正交基[J].辽宁师范大学学报(自然科学版),1987,10(3)：94-96.

[3] 仇永平.合同变换正交化方法[J].曲阜师范大学学报(自然科学版),1988,14(1)：70-75.

[4] 曹锡嗥,等编.高等代数[M].北京：北京师范大学出版社,1987：495-497.

A Method for Finding an Orthonormal Basis by Column Elementary Operation

C H EN Yun-kun, Z HAO Ping
(School of Mathematics and Computer science,Guizhou Normaal University,Guiyang,550025,China)

We present a new method of obtaining an orthonormal basis from a given basis of space Rn.

column elementary transformation;triangular matrix;orthonormal basis

O151.24

C

1672-1454(2011)03-0184-05

2008-08-18;[修改日期]2008-10-21

贵州省科学技术基金项目(黔科合J字L KS[2010]04)