一类直线上自相似集的相似压缩不动点的分布

刘 静, 孙善辉

(宿州学院数学与统计学院,安徽宿州 234000)

一类直线上自相似集的相似压缩不动点的分布

刘 静, 孙善辉

(宿州学院数学与统计学院,安徽宿州 234000)

先构造了一类直线上的自相似集,研究了它的相似压缩不动点的坐标公式.作为推论我们给出了三分Cantor集相似压缩不动点的坐标公式,从而首次发现了它的相似压缩不动点的分布规律.

相似压缩不动点;三分Cantor集;坐标公式

2005年文[1]提出了相似压缩不动点这一崭新的概念,这为探讨自相似集的结构提供了另一个研究方向.我们若可以找到自相似分形的相似压缩不动点,便可以得到自相似集在相似压缩不动点处的局部性质,从而又可以根据相似压缩不动点的处处稠密推出自相似集的性质.可见研究自相似集的相似压缩不动点是当今十分前沿的课题,对认识自相似分形的结构和推动分形几何的发展都具有十分重要的意义.本文研究了一类直线上自相似集的相似压缩不动点的分布,是继相似压缩不动点概念提出后的一个重大突破.

1 相关概念与已知结论

2 一类直线上的自相似集的构造

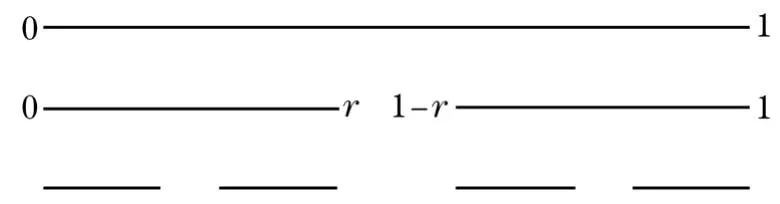
图1 一类推广的Cantor集的构造图

3 E＊的相似压缩不动点的坐标分布

下面我们就来探求E＊的相似压缩不动点的坐标公式.

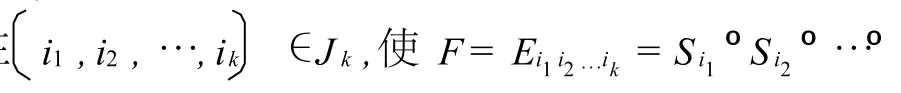
在证明定理1之前我们先考察E＊的第k级压缩与第k+1级压缩得到的相似压缩不动点坐标之间的关系.

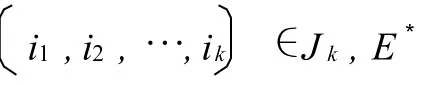
此时定理1结论也成立,综上所述定理1成立.

由定理1我们能得到如下推论:

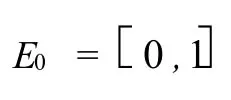
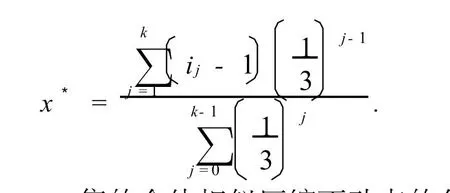
注 由推论1可以找到三分Cantor集的全体相似压缩不动点的分布为

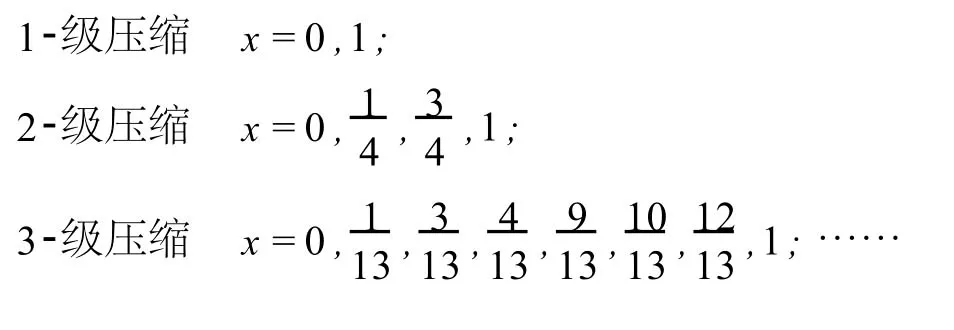
[1] Xu Shaoyuan.Connecting Hausdorff measure and upper convex density orHs-a.e.covering[J].J.Math.Anal. Appl.,2005,311(1)：324-337.

[2] Zhou Zuoling and Li Feng.Twelve open problems on the exact value of the Hausdorff measure and on topological entropy：abrief survey of recent results[J].Nonlinearity,2004,17(2)：493-502.

[3] 许绍元,周作领.关于满足强分离开集条件的自相似集的Hausdorff测度[J].数学进展,2005,34(5)：545-552.

[4] 许绍元,许璐.关于三分Cantor集的构造的一个基本性质及其应用[J].数学实践与认识,2001,31(2)：223-226.

The Exploration of the Contracting-similarity Fixed Points for a Kind of Self-similar Fractal on Straight line

L IU J ing, SUN S han-hui
(Department of Mathematics,Suzhou College,Suzhou,Anhui 234000,China)

We construct a kind of self-similar fractalE＊on straight line firstly,then we research the coordinate formula for the contracting-similarity fixed points ofE＊.As an application,we get the coordinate formula for contracting-similarity fixed points of the middle third Cantor set,so the distribution of the middle third Cantor set is found for the first time.

contracting-similarity fixed points;middle third Cantor set;coordinate formula

O189.1

A

1672-1454(2011)03-0066-04

2008-07-10

宿州学院自然科学研究项目(2009y2k26;2009y2k27)