圆筒型永磁直线电动机电流L2控制

金朝红，李槐树，宋立忠

(海军工程大学，湖北武汉430033)

0 引 言

当前我国国民经济正处于结构转型的关键时期，十二五规划明确提出要对现有制造业进行升级，大力发展先进制造业。直线电动机行业作为基础行业，直线电动机的发展对我国先进制造业意义重大。1983年随着价格相对低廉的钕铁硼永磁材料研制成功，国内外永磁电机的研究开发重点转移到工业和民用电机上。永磁直线电动机(以下简称PMLM)具有体积小、能效高、噪声小、结构灵活和直驱等特点，广泛应用在数控机床、工业机器人、信息与自动化、汽车工业、磁悬浮列车等场合［1］。我国每年稀土产量的三分之二用于出口，剩下的三分之一用于电机的部分也很少，因此我国发展永磁直线电动机有巨大的潜力。由于PMLM的磁场不是闭合的，由此产生了边端效应;永磁直线电动机直接驱动负载，对负载的变化比较敏感;此外，PMLM的机电参数是变化的，如动子质量随时间变化、电感随位置而变化、电阻随温度变化;同时电动机的模型存在未建模和非线性动态，还存在不确定的外部干扰例如负载的变化、摩擦力的不确定性、电机推力的脉动等，这些干扰直接影响到闭环系统的稳态误差、极限环和低通带宽［1］。上述问题使得永磁直线电动机的控制变得比较复杂。为了获得永磁直线同步电动机高精度控制，必须采取有效的控制策略来抑制系统自身参数及外界环境变化产生的扰动，这就要求控制方法有很强的鲁棒性。由于永磁直线电动机系统具有很强的非线性，采用线性系统的控制策略不能获得良好的性能。学者们提出了很多控制策略，比如迭代学习控制［2］、模糊神经网络控制［3］、自适应控制［4－5］、滑模控制［6］等。这些方法有其局限性，比如模糊规则库的建立问题、滑模控制的抖振问题、神经网络的算法复杂性问题。这些问题限制了其应用范围。

本文将参数的不确定性看作系统的干扰，采用非线性L2控制策略，结合LMI方法，设计了L2控制器，使圆筒型永磁直线电动机系统在存在参数不确定性的情况下，在原点平衡点渐进稳定。

1 圆筒型永磁直线电动机的数学模型

1.1 TPMLM的电流方程

我们仅考虑基波分量，在d－q轴坐标系，圆筒型永磁直线电动机(以下简称TPMLM)的电流方程描述［7］:

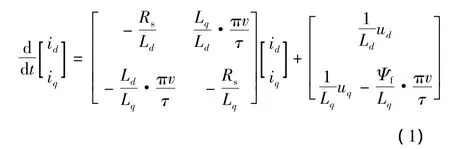
式中:id、iq为TPMLM相电流;ud、uq为TPMLM相电压;v为动子直线速度;τ为极距;Rs、Ld、Lq、Ψf分别为相电阻、d、q轴电感、永磁体基波磁势过动子绕组磁链的实际值为其标称值，其变化量分别为ΔRs、ΔLd、ΔLq、ΔΨf，则有:

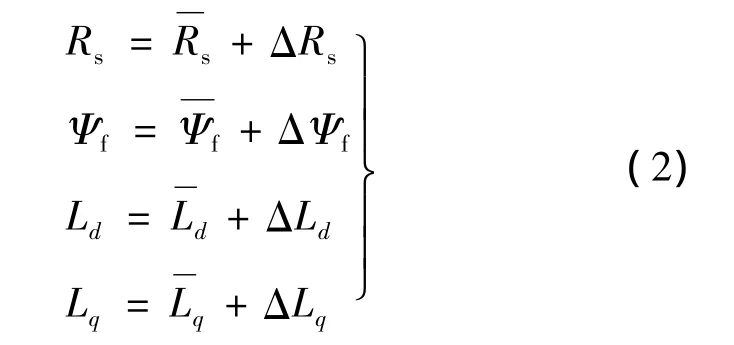
将式(2)代入式(1)，并令x=［x1x2］T=［id－idriq－iqr］T，idr、iqr为d、q轴电流的参考信号。TPMLM的电流状态方程可变成:

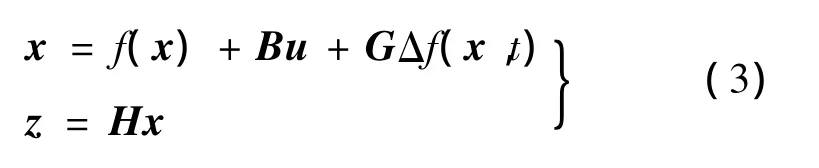
式中:f(x)为单位矩阵，z表示评价信号，H∈ Rp×2，Δf=

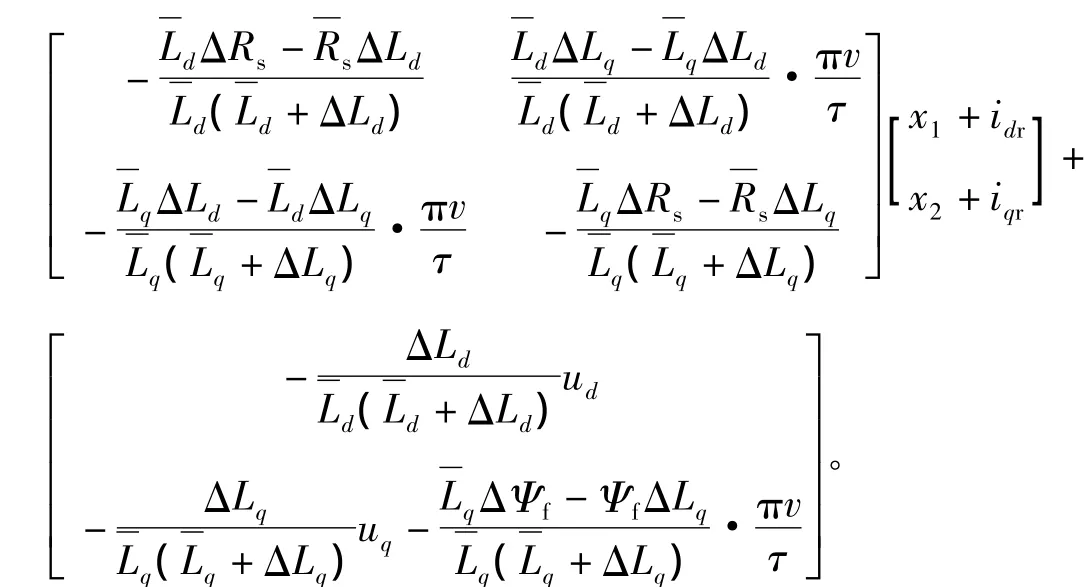
在式(3)中，Δf表示由电机参数的变化引起的系统干扰，可以看出，Δf含有电流分量，因此Δf可以表示由电机参数变化引起的干扰的量化指标。如果我们将电机参数的变化看作施加在电流控制系统上的干扰信号，将电机参数变化引起的电流变化看作干扰信号在系统输出端的输出量，则电机参数变化问题就变成了系统的干扰抑制问题，可以采用L2性能指标来描述此干扰信号的抑制问题。

1.2 TPMLM的动力学模型

TPMLM的动力学模型如下:

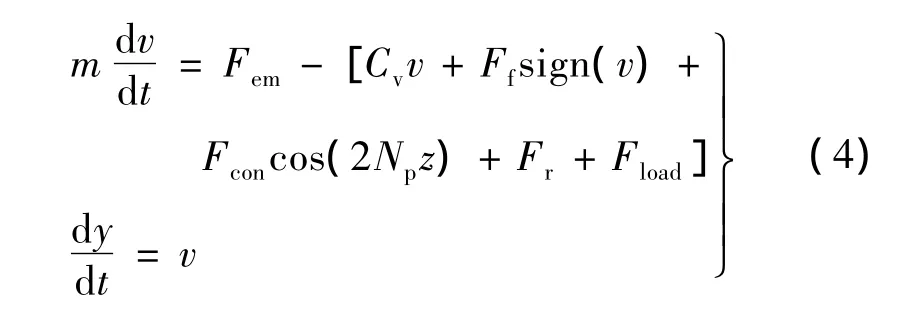
式中:Cv为粘滞摩擦系数;Fconcos(2Npz)为齿槽力;Fr为纹波推力;Fload为负载阻力;Ffsign(v)为静摩擦力;m为动子质量;Fem为电磁推力;v为动子速度;y为动子位移。

令:F=Fem－d，d=Ffsign(v)+Fcogcos(2Npz)+Fr+Fload并对式(4)进行拉普拉斯变换，可得:

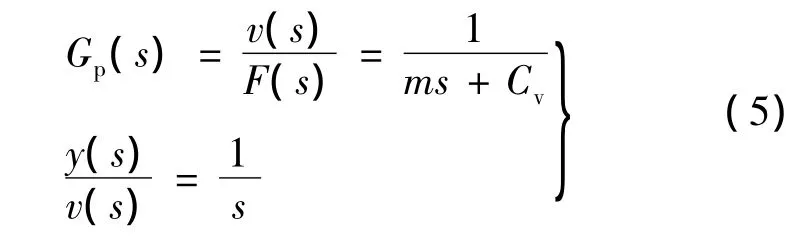
TPMLM电磁推力模型如下:

式中:Kd为推力系数;iq为q轴电流。

由上所述，TPMLM系统的模型如图1所示。

图1 TPMLM系统的模型

2 TPMLM电流控制系统设计

针对式(3)，对TPMLM的L2控制问题可以表述如下:对于给定的正数γ，求状态反馈控制律:

使得闭环系统满足如下性能准则:

(1)当Δf(x，τ)=0时，闭环系统在x(0)=0处是全局渐近稳定的;

(2)对于任意给定的T＞0，当x(0)=0时，不等式:

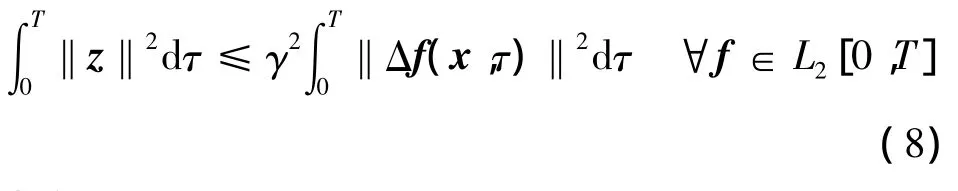
成立。

由γ耗散性与L2性能准则的关系可知，式(8)等价于以下耗散不等式:

其中:V(x)是正定的储能函数。

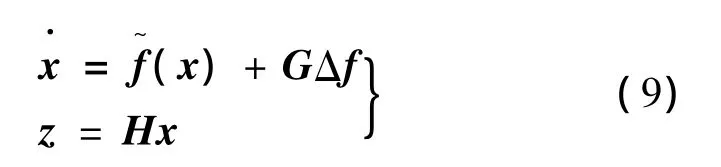
由文献［4－5］可知，如果存在半正定的储能函数V(x)，满足如下HJI不等式:

则闭环系统具有性能准则(2)。本文以下部分将叙述如何将求解HJI问题转化为求解LMI问题，同时使得闭环系统满足性能准则(1)和(2)。

下面采用LMI方法设计TPMLM电流L2控制算法。

设V(x)=xTP－1x为储能函数，其中P∈Rn×n，P=PT＞0，代入式(10)左边，得:

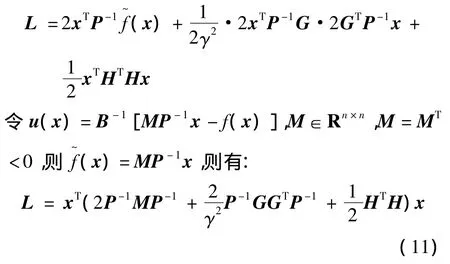
易知存在D∈Rn×n，HTH=DTD成立，式(11)右边乘以P2并将HTH=DTD代入得到:

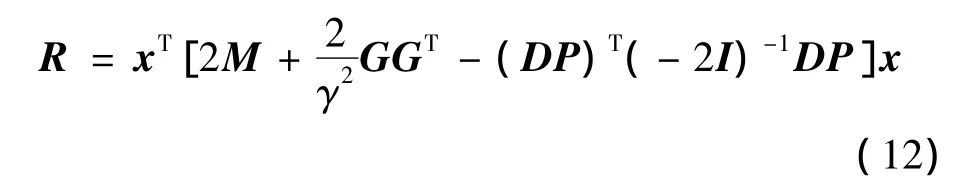
则L=P－1RP－1。由式(10)～式(12)可知，当R≤0时，∀x即:

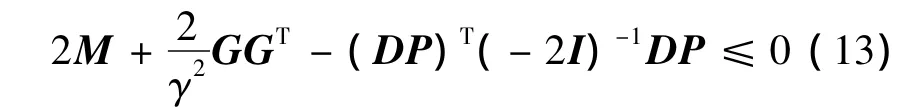
TPMLM电流闭环系统满足性能指标(2)。

由式(13)和Shur定理可得:

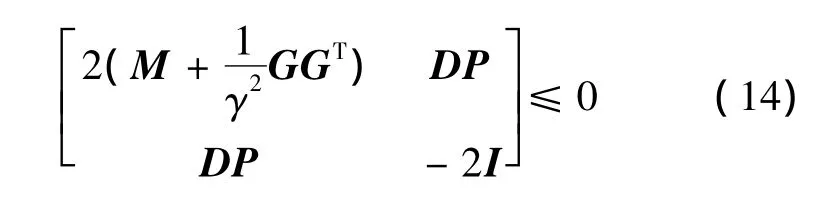
当w=0时，令储能函数V(x)=xTP－1x为其Lyapunov函数，则:

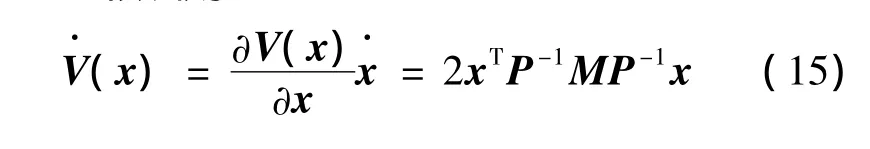
由于P＞0，M＜0，所以V·(x)=2xTP－1MP－1x＜0，x≠0，又因为V(x)是径向无界的，所以闭环系统在x=0处全局渐近稳定。因此TPMLM电流闭环系统具有性能准则(1)。

因此，令式(3)的控制律为u(x)=B－1［MP－1x－f(x)］，TPMLM电流控制系统满足性能准则(2);由式(14)求得P、M满足P＞0，M＜0，则TPMLM电流控制系统满足性能准则(1)。将式(3)代入可得:

M、P可由式(14)求解。

式(14)是非严格LMI，对于可行性问题，对应的严格LMI的解也包含在其解集内。因此求解非严格LMI的可行性问题，可求解对应的严格LMI的可行性问题，在大多数情况下是可行的。运用Matlab中的LMI工具箱或其他计算软件容易求解。

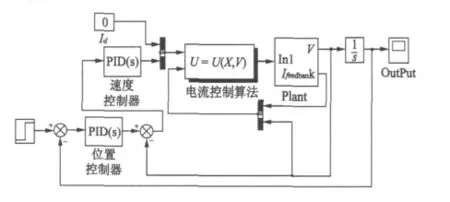
图2 圆筒型永磁直线电动机控制系统仿真模型

3 仿真实例

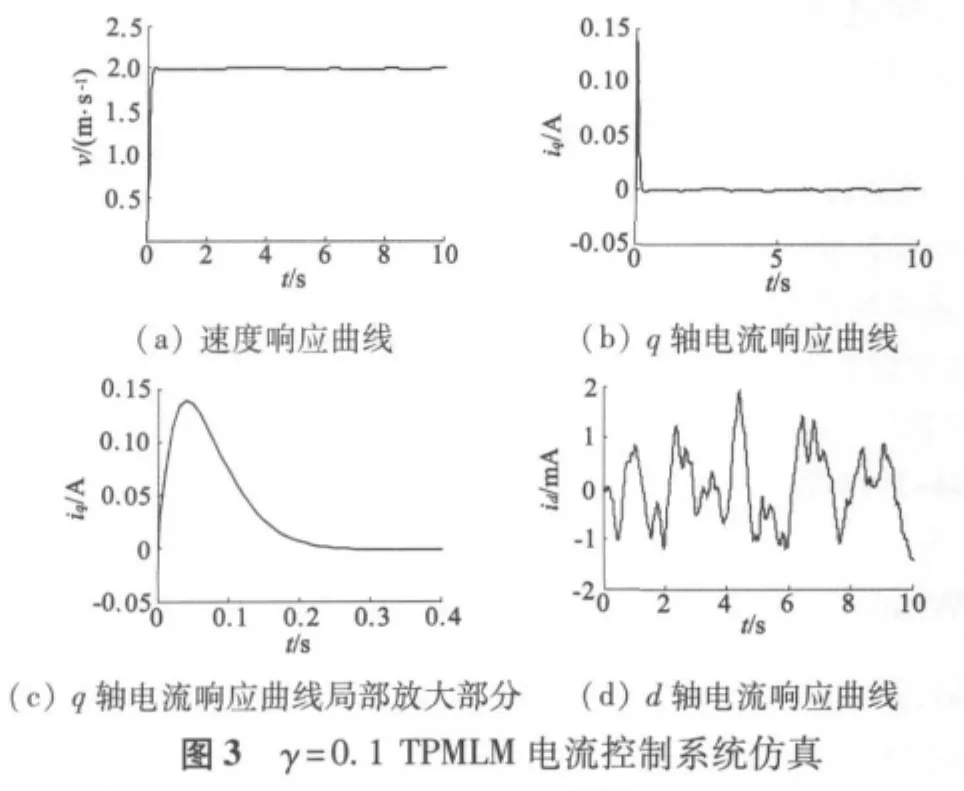
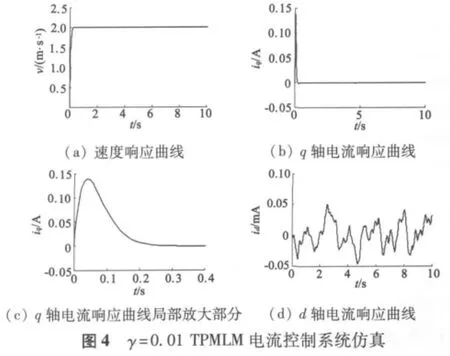
为了验证设计的控制律，针对一台圆筒型TPMLM控制系统进行仿真。样机的主要参数解得由Matlab鲁棒控制工具箱解式(14)得到则控制律得u=仿真时，电机参数的变化在±10%的范围内。设置的初始状态为［idiq］′=［0 0］′，速度设为2 m/s，d轴电流设为0。仿真模型如图2所示。电流控制器仿真模型采用S函数编写，速度控制器和位置控制器采用PI控制算法。本文主要设计电流控制算法，不考虑动力学模型中的干扰d，分别对γ=0.1、γ=0.01的情况下进行仿真。仿真结果如图3和图4所示。

仿真结果归纳如下:

(1)在干扰抑制方面，L2控制器对电机参数变化的抑制效果很好，并且γ越小，电机参数的变化对电流的影响越小。

(2)在控制系统动态性能方面，电流输出响应速度很快，超调量很小，并且与γ的大小关系不大。

4 结 论

针对TPMLPM参数变化引起的干扰，设计了电流L2控制器。将TPMLPM的参数变化看作系统的干扰项，采用状态空间法，在旋转坐标系下建立包含干扰项的的TPMLPM模型，根据所建立的模型，将TPMLPM电流控制器的设计问题转化为L2控制标准问题;最后对于L2控制标准设计问题，选取二次型函数作为HJI不等式存储函数，采用线性矩阵不等式方法，推导出了电流控制器的解析表达式，并且证明了该闭环系统是渐进稳定的。针对由于TPMLPM系统参数变化引起的不确定性，仿真和实验研究表明L2控制策略能够抑制TPMLPM参数变化对电流的影响，实现了对电流的有效控制，进而实现了对电磁推力的有效控制，为圆筒型永磁直线电动机的直线运动控制创造了重要条件。

［1］ 叶云岳.直线电机技术手册［M］.北京:机械工业出版社，2003.

［2］ Butcher M，Karimi A.Linear Parameter－Varying Iterative Learning Control With Application to a Linear Motor System［J］.IEEE/ASME transactions on mechatronics，2010，3(15):412－420.

［3］ Lin F J，Shen P－H.Adaptive Fuzzy－Neural－Network Control for a DSP－Based Permanent Magnet Linear Synchronous Motor Servo Drive［J］.IEEE transactions on fuzzy systems，2006，4(14):481－495.

［4］ Liu T H，Lee Y C，Chang Y H.Adaptive Controller Design for a Linear Motor Control System［J］.IEEE transactions on aerospace and electronic systems，2004，2(40):601－616.

［5］ Su W T，Liaw C M.Adaptive Positioning Control for a LPMSM drive based on adapted inverse model and robust disturbance observer［J］.IEEE Transactions on Power Electronics，2006，21(2):505－517.

［6］ Francesco C，David N，Ernesto M，et al.Sliding－Mode Control With Double Boundary Layer for Robust Compensation of Payload Mass and Friction in Linear Motors［J］.IEEE Transactions on Industry Applications，2009，45(5):1688－1696.

［7］ 郭庆鼎，王元成，周美文，等.直线交流伺服系统的精密控制技术［M］.北京:机械工业出版社，2000.