基于动态差分GPS的滑坡位移监测系统

雷 波,陈华德,李 青,李 雄

(1.中国计量学院机电工程学院,浙江杭州310018;2.浙江省计量科学研究院,浙江杭州310013)

我国是一个地质灾害众多的国家,其中大多数山地灾害又以滑坡为主要表现形式.据国土资源部和中国地质环境监测院统计,2010年全国共发生了30 670起地质灾害,其中滑坡22 329起,造成数千人死亡或失踪,直接经济损失63.9亿元[1].

目前国内对滑坡位移的监测方法主要有TDR监测法、INSAR监测法、分布式光纤传感技术监测法、测量机器人监测法、遥感监测法、GPS监测法和电磁互感监测法等[2,3],其中GPS监测的方法具有自动化程度高,观测速度快,定位精度高,观测点间无需通视,全天候作业等优点.经过多年的发展,GPS测量技术已从静态测量,快速静态测量,后处理高精度测量,发展到了动态的实时RTK测量模式,测量精度从亚米级发展到了厘米级甚至毫米级.但是一味的追求高精度监测,势必会造成人力和物力的浪费,目前国内已有毫米级测量的系统用于桥梁施工监测和大地测量,但是整个系统的造价昂贵,一般至少在10万元人民币.综合以上考虑,低成本的厘米级动态实时RTK测量在滑坡位移监测中的应用较为合理.本文基于动态差分GPS算法,结合实际项目野外应用中的高度自动化、全天候测量等要求,设计了一种滑坡位移监测系统,监测现场通过GPRS将数据传输至监控中心的计算机,然后通过编写的界面软件实时解算出基线长度,为滑坡预警预报提供科学的依据和评价.

1 系统组成及工作原理

该系统的组成如图1中,系统的测量核心为两个低价位的具有对载波相位观测的单频GPS接收机并分别配以国产测量型天线,将其中一个固定在滑坡体附近的稳定的位置作为参考站,另外一个安置在待测的滑坡体上作为移动站.两站同步对卫星进行观测,移动站通过短距离无线模块将原始数据传输至位于参考站的数据采集模块,数据采集模块则将同时采集到的两站数据通过GPRS方式一并传送到远端监控中心,然后在计算机上进行实时计算.

图1 系统组成Figure 1 Structure of the system

1.1 GPS接收机部分

由于厘米级的动态差分算法是以载波相位作为观测量,所以对接收机的要求是能够对载波相位进行观测并将原始数据输出,但接收机对载波相位观测的质量也会一定程度上影响整个系统的精度.该系统中参考站和移动站均选用Hemisphere公司的单频OEM 板卡作为GPS接收机,在高精度的测量中,整个系统对天线的要求相应也会较高,主要从天线的方向性、极化形式、频率特性、增益等几个方面进行考虑.

1.2 数据传输部分

动态的载波相位差分技术也叫 RTK技术[4],是差分GPS技术与数据传输技术的结合.其基本原理是建立在实时处理参考站和移动站观测到的载波相位基础上的,所以系统对数据传输部分的传输速率和数据可靠性要求较高.

本文中的数据传输将分为两个部分:一是移动站的原始数据向参考站中的数据采集模块的传输,另一个则是参考站中数据采集模块把采集到的两站数据一同向远方监控中心的传输.考虑到移动站与参考站之间的距离较近,所以用短距离无线传输模块就可以实现移动站数据向参考站的传输[5].而参考站与监控中心之间距离较远,要求有较强的通信能力,目前主要有数传电台(VHF)、GSM/GPRS网络、CDMA 网络等方式.数传电台虽然不产生通讯费用,不受无通讯条件的限制,但传输距离受限,故本系统采用具有高速率、永远在线、按数据流量计费等优点的GSM/GPRS网络[6].根据GPRS连接的特点,参考站GPRS模块在上电时就登陆GSM网络,然后通过PPP协议获取动态分配的IP地址,并主动与监控中心具有固定IP地址的计算机建立连接,之后就可以进行数据的双向通信了.

1.3 数据处理部分

首先位于参考站的数据采集模块对移动站和参考站的原始数据进行必要的预处理,剔除掉错误的数据,对于正确可靠的数据加上测站标记以区分,并打包,然后通过GPRS进入Internet网络将两站的原始数据上传给监控中心的计算机,最后的数据处理工作则是由计算机完成.

2 载波相位差分算法

载波相位差分定位的原理是将两台GPS接收机其中一台固定在已知的位置作为参考站,另一台安置在待测的目标上作为移动站,两站同时对共视的卫星进行观测并以载波相位作为观测量.对于载波相位来说,测量精度可达0.5～2.0 mm[7],但是在测量过程中会受到多种误差的影响,使得精度大大降低.由于GPS测量中的误差对两个同步观测站观测相同的卫星会有较强的相关性,所以将两站的观测量进行不同的线性组合是一种简单有效消除或减弱误差影响的方法,目前主要有单差、双差和三差三种形式.三差模型中使得观测方程的数目明显减少,数据的利用率降低,不利于最后结果的解算,所以一般常采用站际、星际双差模型.

2.1 站际、星际双差观测模型

设参考站T1和移动站T2同时对卫星Si和Sj进行观测,先将两站对卫星Si的观测方程求差得到站际单差(t),同样对卫星Sj也会有站际单差(t),然后将两颗卫星的站际单差再求差得到站际、星际双差(t).

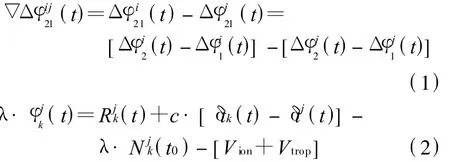
将载波相位观测量方程(2)代入以上双差式中可得到双差观测方程

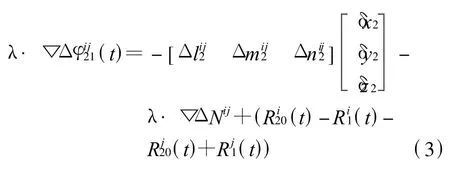
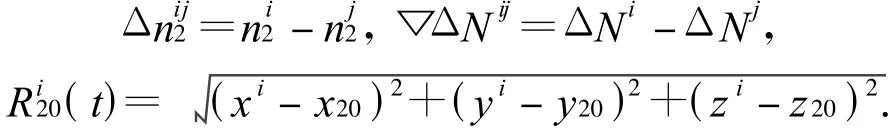
式中:(x20,y20,z20)为移动站的初始概略坐标,由GPS接收机的输出可直接得到.

从上式双差观测方程中,可以看到接收机和卫星的钟差的影响都已消除,电离层折射和对流层折射的影响在短距离内也可以完全消除,这就是站际、星际双差模型的优点.

考虑到滑坡多发生在山区,可观测到的卫星的数量将会一定程度上受到影响,在这里选取5颗结构较好的共视卫星进行解算.当两站接收机在历元 t1和t2同时观测这5颗卫星,则可组成八个方程式,七个未知数的双差观测方程组,

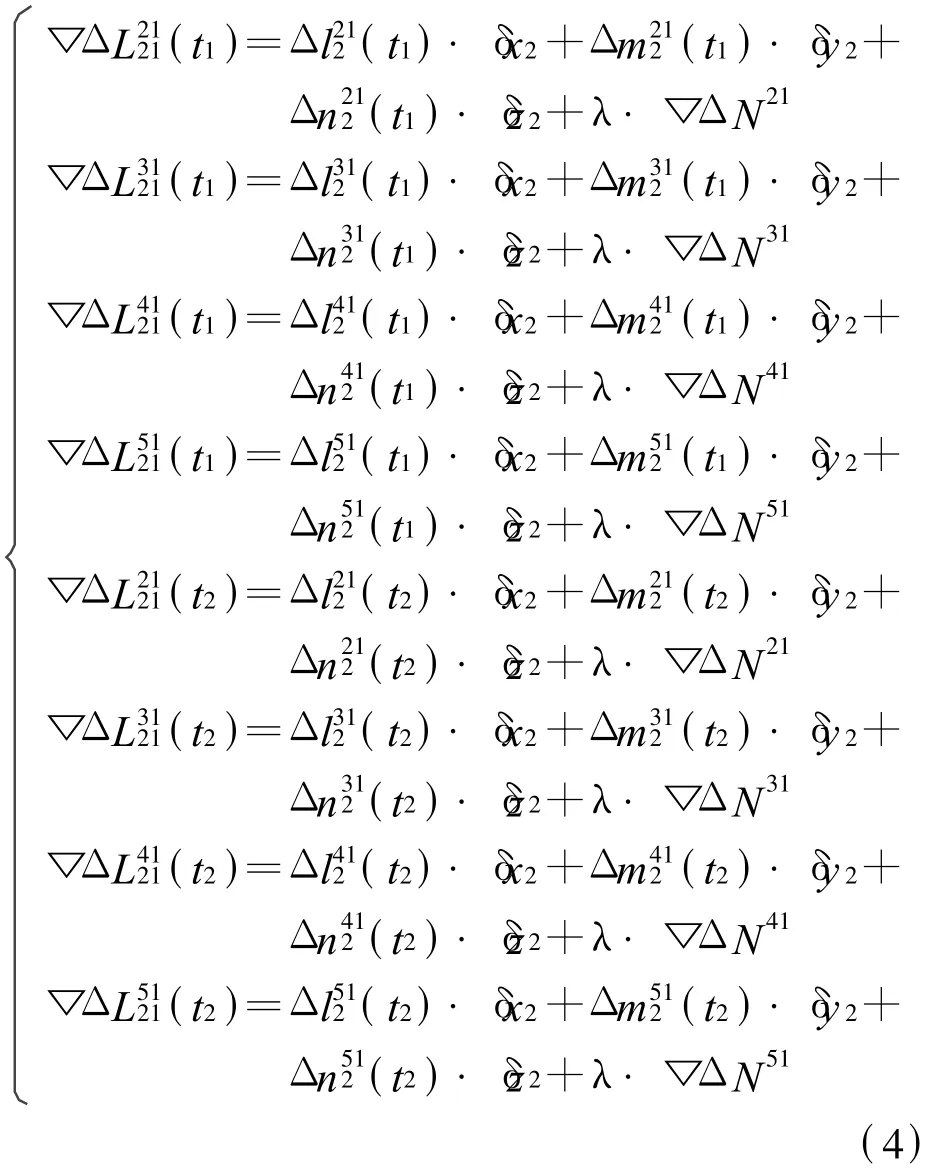
式中,

将以上方程组(4)化成矩阵形式

式中:

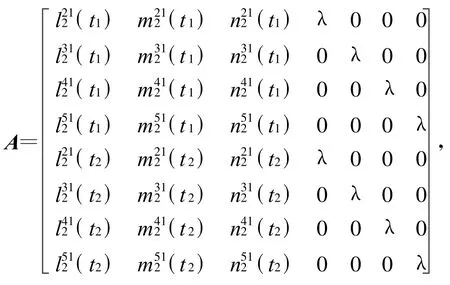
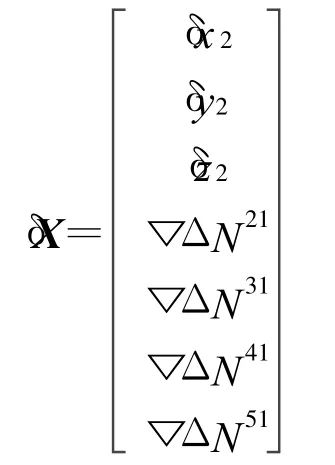
求解该矩阵方程可得最小二乘估计解:

又相同历元内的双差观测值具有较强的相关性,而不同历元之间又是互不相关的,所以取权逆阵:

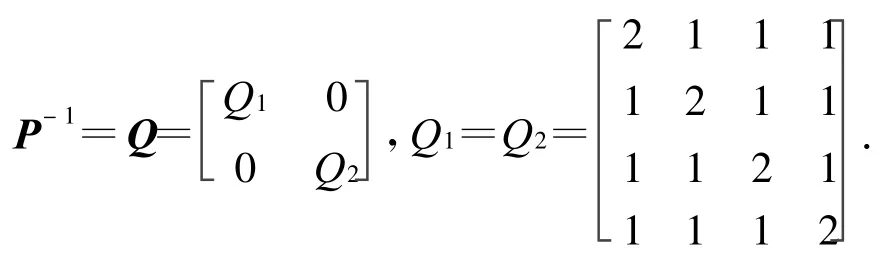
2.2 整周模糊度的固定

通过求解上述方程组得到双差模糊度(▽ΔN21,▽ΔN31,▽ΔN41,▽ΔN51)的实数解,但是根据整周模糊度的整数特性,双差模糊度也应该是一组整数值,但也不能对双差模糊度的实数解进行简单的取整.因为观测时间较短时,卫星空间结构变化较小,导致初始解中的实数模糊度参数精度较低.整周模糊度的精确求解是载波相位测量中的关键问题,目前较广泛采用的方法主要有FARA、模糊度函数法、最小二乘收索法和最小二乘降相关平差法(LAMBDA)[7].这些方法中所采用的搜索算法、搜索区域的大小、判断标准和所加的约束各不相同.

本文采用经典的LAMBDA算法对整周模糊度进行求解.该方法是目前快速定位中最成功的一种模糊度搜索方法,其基本原理在相关文献中都有介绍,计算过程如下:

1)首先对初始解中的模糊度实数解 ^N及其协因数阵Q^N进行整数变换.

2)采用搜索算法在变换后的搜索空间求解,由于变换后的新参数的方差及相关性都有很大的减小,所以搜索速度更快.

3)在得到最优的整数组合后,再进行逆变换可得到最终要求解的最佳整周模糊度的整数解.

4)将这组最佳模糊度整数解固定,在以后求解基线向量的过程中都把它作为已知数,则同样共视5颗卫星,只需一个历元就可求出基线向量,式(4)中的方程数量减少一半,未知数减少到只有3个.

2.3 定位星的选择

由于在GPS定位过程中,接收机所观测到的卫星的空间几何结构也会影响最终定位的精度,所以通常的做法是从可见卫星中选取几颗结构较好的来进行定位,在相关文献中已有一些选星的方法,这些方法大都是为了减少计算量而设计的.由于本文所设计的系统最后的解算工作是在计算机平台上进行的,所以完全不用担心计算量的问题.采用最佳选星法[8],从可见卫星中选取5颗星,分别计算所有组合的GDOP值,最后取最小GDOP的5颗星组合作为定位星.并且在构造双差方程组的时候,选取高度角最大、可观测时间较长的一颗卫星作为基准星,然后将其余4颗卫星的单差观测方程分别减去基准星的单差观测方程组成双差观测方程.

2.4 算例分析

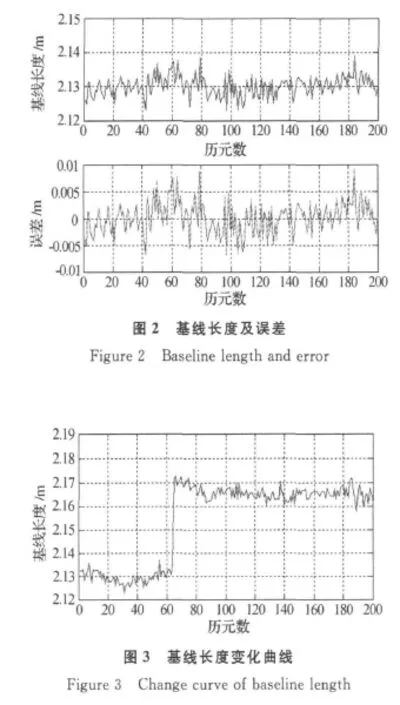
在中国计量学院某楼上将两站天线任意选址固定,在固定后测得基线精确长度为2.13 m.然后两站接收机同步对卫星进行观测数据采样率为5 s.由于在GPS差分定位中对参考站坐标的要求并不高,误差可以允许在10 m以内[9],且本系统所采用的GPS板卡的单机定位精度达到1 m左右,所以可以首先通过几分钟的观测取接收机输出的定位坐标的平均值作为参考站的精确坐标.观测过程中由于受到周围高楼的影响,此时两接收机能同时观测到7颗卫星(PRN分别为:2,4,10,12,13,17,23),通过计算选取最小GDOP组合(PRN:4,17,12,10,23)作为定位星,选取高度角最大的PRN10卫星作为基准星建立双差方程进行平差计算.利用LAMBDA算法搜索双差整周模糊度并将其固定,最后在连续观测的情况下解算出基线的长度.解得的基线长度及其误差如图2,从图中可以看出基线长度基本是在精确值±5 mm范围内变化.

在另一时间同样将两站天线固定在相同的位置,待静止观测一段时间后,将移动站天线在不影响其观测的情况下向远离参考站天线的方向移动3 cm后固定,并继续观测.此时解得的基线长度如图3,可以看出测量精度基本具有厘米级效果.

3 软件实现

软件的设计及实现是整个系统中的主要部分,首先参考站的数据采集模块在上电时就通过串口控制GPRS模块登陆GSM网络并通过PPP协议获取动态分配的IP地址,然后主动与已知IP地址的远端服务器建立连接,之后连接得以保持,等待监控中心下达命令.监控中心计算机在连接建立以后,就可以请求接收机输出所观测到的原始数据,并按照差分GPS原理解算基线长度.图4中给出了服务器端软件计算流程:

在研究以上差分 GPS算法的基础上通过VisualC++6.0编写Windows平台下界面软件,运用多线程和网络编程技术,实现数据的实时通信与并行处理,并使用C++与MAT LAB混合编程[10],很方便地实现了算法中矩阵的运算.最后将基线长度的变化曲线实时显示.

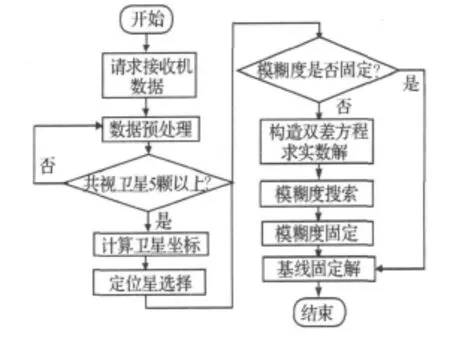
图4 计算机软件流程Figure 4 Flowchart of computer software

4 结 语

运用GPS测量的高度自动化、全天候、测量精度高、观测点之间无需通视的特点,选用低价位的单频GPS接收机作为测量核心,以GPRS作为通讯手段,通过编写动态差分GPS解算程序设计了一套低成本滑坡位移监测系统.试验结果表明该系统能够满足监测的要求,并具有无人值守的优势,证明了该系统在滑坡位移监测中的实用性.

[1]中国地质环境监测院.全国地质灾害通报(2010年)[EB/OL].(2011-01-18)[2011-04-20].http://www.cigem.gov.cn/down.asp？FileName=pdf/2011-1/2011118174421496.pdf.

[2]蒋兴超.滑坡地质灾害监测方法概述[J].长江大学学报:自然科学版,2010,7(3):345-347.

[3]杨 杰,李 青.地下位移实时监测系统研究[J].中国计量学院学报,2008,19(1):41-46.

[4]黄丁发,熊永良,袁林果.全球定位系统(GPS):理论与实践[M].成都:西南交通大学出版社,2006:196-197.

[5]施 阁,卢江丽,孙延伟,等.航模动力及飞行环境无线实时监测系统设计[J].中国计量学院学报,2009,20(1):22-26.

[6]李弘洋,李 青,李 雄,等.全自动远程虹吸式雨量计的研制[J].中国计量学院学报,2010,21(1):32-37.

[7]李天文.GPS原理及应用[M].2版.北京:科学出版社,2010:112-114.

[8]袁社旺,卓 宁.GPS中一种选星方法及实验分析[J].中国惯性技术学报,2008,16(4):445-447.

[9]李征航,黄劲松.GPS测量与数据处理[M].2版.武汉:武汉大学出版社,2010:165.

[10]刘 维.精通 Matlab与 C/C++混合程序设计[M].北京:北京航空航天大学出版社,2005:179-186.