数学建模最优化理论探讨*

方建卫

(西南大学育才学院 理工学院，重庆 401524)

数学建模最优化理论探讨*

方建卫

(西南大学育才学院 理工学院，重庆 401524)

结合2011年“高教杯”全国大学生数学建模竞赛题目A，分析了数学建模的理论思想，提出了数学建模的本质特点实际就是一种最优化的思想。并且通过该比赛题目探讨了用最优化的理论求解数学模型的方法。

数学建模;最优化理论;重金属污染空间分布;单因素模型;模糊神经网络

从大学数学到现代数学，广泛应用于各行各业无论是从纯数学本身的理论，还是从应用数学的相关课题，每一个数学概念的产生都有着很强的实际背景，都是从实际问题中抽象出一般的理论，又用成熟的理论去指导实践，解决实际问题，所以数学概念的产生是确确实实地从实际中来又到实际中去的辨证思想的体现。本文结合2011年“高教杯”全国大学生数学建模竞赛题目A，分析了数学建模的理论思想，提出了数学建模的本质特点就是一种最优化思想。通过matlab5.3，excel软件和修正shepherd插值法拟合出城区的空间分布。数学与信息、计算机技术结合，使得实际问题得到更好更方便的解决。

一、数学建模是数学应用的一种体现

人们常对实际事物建立种种数学模型，以期通过对该模型的考察来描述、解释、预计或分析出与实际事物相关的规律。数学模型(Mathematical Mode1)也是一种模拟，是用数学符号、数学式子、程序、图形等对实际课题本质属性的抽象而又简洁的刻画，它或能解释某些客观现象，或能预测未来的发展规律，或能为控制某一现象的发展提供某种意义下的最优策略或较好策略。数学建模就是用数学语言描述实际现象的过程。因为对于同一个问题可建立不同的实际模型，可得到不同的“最优解”，所以数学建模没有最好，只有更好，关键看建立模型的独特之处。综合起来讲，数学建模的过程可以概括为如下的流程:观察实际问题——提出假设——建模——求解——检验——修改或应用。实际问题经常是十分复杂的，既存在着必然的因果关系也存在某些偶然的因果关系，这就需要我们从错综复杂的现象中找出主要因素，略去次要因素，确定变量的取舍并找出变量间的内在联系。学习数学建模和参与建模实践，实际上是一个综合能力、综合素质的培养和提高的过程。

二、数学模型到最优化理论

2011年“高教杯”全国大学生数学建模竞赛题目A:随着城市经济的快速发展和城市人口的不断增加，人类活动对城市环境质量的影响日显突出。对城市土壤地质环境异常的查证，以及如何应用查证获得的海量数据资料开展城市环境质量评价，研究人类活动影响下城市地质环境的演变模式，日益成为人们关注的焦点。

按照功能划分，城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等，分别记为1类区、2类区、……、5类区，不同的区域环境受人类活动影响的程度不同。

现对某城市城区土壤地质环境进行调查。为此，将所考察的城区划分为间距1公里左右的网格子区域，按照每平方公里1个采样点对表层土(0～10厘米深度)进行取样、编号，并用GPS记录采样点的位置。应用专门仪器测试分析，获得了每个样本所含的多种化学元素的浓度数据。另一方面，按照2公里的间距在那些远离人群及工业活动的自然区取样，将其作为该城区表层土壤中元素的背景值。

所给数据有采样点的位置、海拔高度及其所属功能区等信息，8种主要重金属元素在采样点处的浓度，8种主要重金属元素的背景值。

建模要求:给出8种主要重金属元素在该城区的空间分布，分析该城区内不同区域重金属的污染程度。

模型采用:根据题目给出取样点的位置及其所属的功能区，八种主要重金属元素在各个功能区的浓度，通过matlab5.3数学软件和修正shepherd插值法拟合出城区的空间分布，并运用excel软件分析，计算出各个重金属元素的平均值和标准偏差，然后将处理得到的数据和跟背景值的数据进行对比分析，最终得出不同地域重金属的污染程度。

图1 As元素在该城区分布等高线及散点图

要求八种重金属元素在该城区的空间分布，运用matlab5.3作散乱节点的插值计算，用带有e01sef和e01sff两种函数的修正shephard法插值拟合出该八种元素在该城区的空间分布，空间分布图(以As元素为例):

图2 As元素在该区分布地形图

先由数据拟合发现每种重金属元素都近似服从正态分布，因此建立正态分布模型:

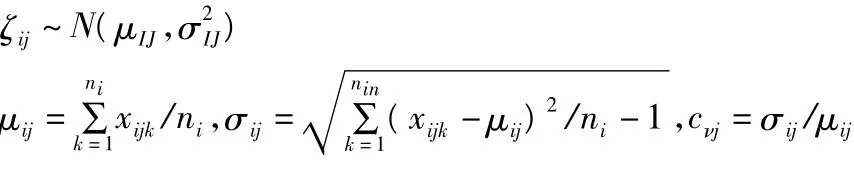
i代表五个功能区(i=1，2，……，5分别代表生活区、工业区、山区、主干道路区、公园绿地区);j代表八种重金属元素(j=1，2……，8 分别代表 As、Cd、Cr、Cu、Hg、Ni、Pb、Zn元素);k第k个样本的浓度;所有样本的总量;ni第i个功能区的样本总量;xjk第j种金属元素第k个样本点的浓度;μij第i个功能区的第j个元素含量平均值;σij第i个功能区的第j个元素含量的标准差;xijk第i个功能区第j种金属元素第k个样本点的浓度 ;cνj第j种金属元素的变异系数;ρij第i个功能区第j种金属元素的污染指标。

模型的优点:针对于其重金属元素成正态分布模型，采用单因素法对其进行评价，提高了模型的精确性。模型的缺点:模型较为单一，缺少对照模型。而且拟合的数据亦缺少精确性比较。

若采用神经网络模型可根据土壤金属污染评价的需要以及模糊机理和人工神经网络的特点，构建了如下图所示的模糊神经网络、模糊神经网络的结构及两个主要的功能模块:模糊化模块和人工神经学习推理模块。

这个数学模型亦很好解决不同地区重金属污染程度的情况。总之，数学建模与最优化理论之间是相辅相成的，数学模型来源于生活和实践，而实践中的问题总是层出不穷的，建立的模型也可能会越来越庞大复杂，任何一个模型的建立，都会使最优化模型的求解越来越优，会给实际问题带来突破性的进展。故有了解问题的起源和实际背景，了解这一理论发展的迂回曲折、螺旋式的前进，才会更深刻地领悟到一种理论的思想本质，领悟到它的精髓，慨叹它的美妙!

［1］杨启帆.数学建模［M］.杭州:浙江大学出版社，2005.

［2］胡运红.非线性最优化问题及其算法研究［J］.运城高等专科学校学报，2003，(6).

［3］中国环境监测总站.中国土壤元素背景值［M］.北京:中国环境科学出版社，1990.87.

［4］方凤满，王起超，李东侠，等.长春市大气颗粒污染特征及影响因子分析［J］.环境科学学报，2001，(3).

G642

A

1006－5342(2011)09－0167－02

2011－06－20