结构损伤检测中的应变类模态技术方法

陈宇翔

(和记黄埔地产武汉分公司，湖北 武汉 430022)

涂金钊

(海南雅克设计有限公司，海南 海口 570125)

结构损伤检测中的应变类模态技术方法

陈宇翔

(和记黄埔地产武汉分公司，湖北 武汉 430022)

涂金钊

(海南雅克设计有限公司，海南 海口 570125)

结构的应变类模态对结构损伤具有很高的敏感性。从基于应变类模态技术入手，详细介绍了各种基于应变类模态技术的损伤识别方法，同时对应变类损伤识别方法存在的局限性进行了总结，为结构的损伤诊断提供参考。

模态分析；损伤检测；振动；应变模态

结构在一定环境条件下会出现损伤，损伤将改变结构的强度和刚度从而引发更大的结构损伤积累，这将导致结构的突发性失效，从而使结构的安全受到威胁。因此，结构损伤识别成为国内外学者关注的焦点。由于基于振动理论的振动法诊断技术具有经济有效、使用安全等优点,近几十年来成为国内外研究的热点。研究表明[1],以应变类参数为基础的损伤定位方法明显优于以位移类参数为基础的损伤定位方法。同时，根据圣维南原理可知，远离损伤区域的结构应变变化则不明显，因此，结构在局部的应变具有对局部损伤敏感的特点。L.H.Yam等[2]通过位移模态微分运算方法推导并论述了应变模态相关理论。下面，笔者对结构损伤检测中的应变类模态技术方法进行阐述。

1 应变类模态的损伤识别的直接方法

1.1应变模态差法

最为直接的损伤定位准则是依据损伤发生前后的结构应变模态差的绝对值,即：

(1)

首先寻找各阶应变模态差的最大绝对值,再寻找整个应变模态差矩阵的最大值,其所对应位置即为最有可能发生损伤的位置,并按“少数服从多数”的原则确定最终损伤位置。

1.2应变模态变化率法

由于结构损伤前后的位移模态发生变化,应变模态作为其一阶导数将发生突变,则应变模态变化率应为更加敏感的指标[3]。

方法1 单元k的第r阶应变模态变化率：

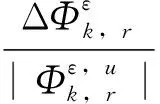
(2)

方法2 节点j的第r阶应变模态变化率：

(3)

1.3坐标应变模态确认准则及其改进方法

坐标应变模态确认准则是基于相关性原理得到的,其相关系数可表示为：

(4)

式(4)实质上是位移坐标模态保证准则[4]的改进。结构损伤前，相关系数为1；若相关系数趋近于0或较小时，说明结构可能存在损伤。实际上，该准则存在一定的不合理性，因为损伤对各阶应变模态的影响是不同的,而此处却将各阶模态值平均化加以考虑。

考虑到应变模态对局部损伤敏感的特性,采用基于局域特征变化的损伤定位准则应该更为合理[5]。通过对坐标k及其邻域δ(k)中的其他坐标求和后来寻找相关系数的最小值进行损伤识别，可表示为：

(5)

式中，δ(k)为反映局域特征变化的局域值，一般根据实际情况可取1或2。

依据改进后的确认准则，首先寻找所有相关系数的较小值所对应的位置，然后按“少数服从多数”的原则方法对各阶模态分别进行考虑。

1.4应变模态的结构损伤识别直接指标法

1)损伤位置直接指标法 应变模态在结构损伤处存在极值并发生突变，但进行光滑处理过的应变模态曲线则可导。通过差分及三次样条插值算法，可求出光滑应变模态差分曲线。

对某阶应变模态差分曲线，若任意相邻两极值符号相异，则它们之间有且仅有一个零值点，该极值点定义为有效极值点，不计支座附近的零值点定义为有效零值点。假定存在有效零值点l1，l2，…，lp，其有效极值点x0，x1，x2，…，xq，有效极值y0，y1，y2，…，yq，(q≥P)。根据有效零值点数将有效极值点分组，对应于有效零值点lj的左右有效极值点和有效极值分别记为xj1、xj2和yj1、yj2，若相邻2个有效零值点lj-1和lj间不存在无效极值点，则y(j-1)2=yj1，否则y(j-1)2≠yj1[6]。

若定义LSMSD(j)为某阶应变模态差分曲线第j个有效零值点损伤位置直接指标值，则有：

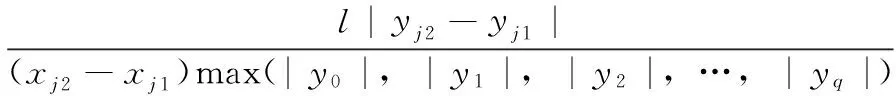
(6)

由此可知，若LSMSD(j)值越大，则lj点损伤的可能性越大，再结合差分曲线的变化规律便可判断损伤位置。

2)损伤程度直接指标法 应变模态曲线仅在结构损伤处及附近存在突变，故可利用损伤非影响区的应变模态数据拟合出完好状态下的应变模态曲线。根据研究[7]得知，结构损伤程度越严重，损伤影响区越大；同一损伤量下，损伤面积与损伤位置有关。故可定义应变模态损伤面积与拟合出的完好面积的比值定义为局域应变模态面积损伤程度指标，该指标与损伤量有较好的对应关系。影响区损伤曲线与横轴所围面积定义为应变模态剩余面积，则完好面积应为应变模态损伤面积与剩余面积之和。

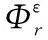
(7)

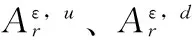
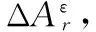
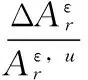
(8)

该损伤程度直接指标具有以下特点：①随损伤程度增加呈单调递增趋势；②该指标与损伤位置无关，与应变模态阶数无关，与是否归一化无关。

1.5应变模态敏度比指标法

(9)

定义结构损伤前后k节点的第r阶应变敏度比为：

(10)

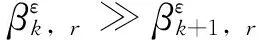
1.6结构损伤位置识别的组合指标法

滕海文等[9]以动力响应的应变模态指标为基础，结合频率指标提出对结构损伤位置识别的组合指标。

定义1应变模态变化与固有频率变化平方的比值为组合指标C1:

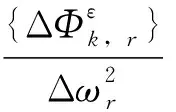
(11)

定义2应变模态与固有频率平方比的变化量为组合指标C2:

(12)

定义3应变模态变化与固有频率平方变化率的比值为组合指标C3:

(13)

1.7广义应变比能指标

在应变模态的基础上，刘文峰等[10]提出以广义应变比能进行结构的损伤识别。

(14)

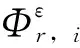
当某处的w值突然增大时，即可认为该处具有损伤，wi的极大值处可认为是损伤部位，则可以定义广义应变比能比值：

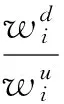
(15)

如果结构完好，那么Di的值应该在1附近，结构损伤时同样也可以通过选取Di的极大值处，认为其为损伤的部位。

2 应变类模态的损伤识别的间接方法

2.1基于灰色相关性的损伤定位理论

根据灰色相关性理论，结构未损伤时，其上各节点的模态曲率相关性系数为1；结构损伤后，损伤部位的模态曲率相关系数小于1，因此模态曲率的相关程度可以反映结构是否发生损伤[11-12]。应变模态同曲率模态一样，对结构的损伤具有一致的敏感性。

令X为灰色关联因子集，xu∈X为未发生损伤时各节点振动位移模态，即为参考序列；xd∈X为结构发生损伤后各节点振动位移模态，为结构损伤后的比较序列:

xu=(xu(1)，xu(2)，…,xu(n))xd=(xd(1)，xd(2)，…，xd(n))

则ξ(k)为两者在k点的灰色关联系数[13]:

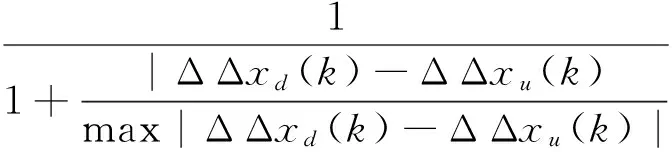
16)

式中，ΔΔxu由参考序列二次累减生成；ΔΔxd由比较序列二次累减生成；ρu(k)、ρd(k)分别为参考序列xu与比较序列xd在k点的曲率模态值，可以通过中心差方法求得:

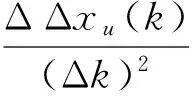
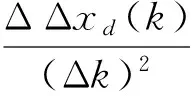
由式(16)可知，灰色曲率模态关联系数变化区间为0.5≤ξ(k)≤1；通过对式(16)进行修正[14]，使得反映损伤位置的参数(SDCACk)变化区间为0.27～1.0，显然，损伤位置变得更加突出。

定义结构节点的位移曲率模态置信因子(SDCACk)，即：

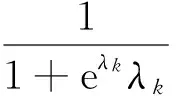
(17)

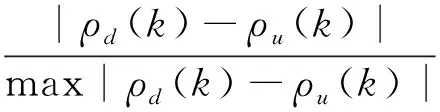
2.2基于神经网络的两阶段损伤诊断方法

瞿伟廉等[15]对一框架节点进行数值模拟，提出了一种基于神经网络技术的2步诊断法。

步1 将结构划分为多个子区域,将有损伤结构的前n阶模态频率变化比与结构损伤子区域的关系输入概率神经网络,进行损伤子区域判定。

由摄动理论可知,结构发生损伤后的任意两阶频率改变量之比仅是损伤位置的函数,而与损伤大小无关因此,只需测试结构损伤前后的前几阶自振频率,便可确定结构损伤的位置。定义结构频率变化比为:

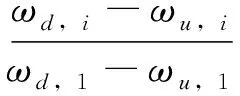
(18)

式中，ωu,1、ωu,i、ωd,1、ωd,i分别为结构损伤前、损伤后第1阶和第i阶自振频率。

步2 将损伤子区域内结构前二阶杆端应变模态变化量与节点损伤位置和损伤程度的关系输入径向基神经网络,进行损伤位置和程度的具体诊断。定义结构的杆端应变模态变化量：

(19)

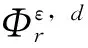
2.3基于改进遗传算法的结构损伤大小识别

由于单元的应变对于结构的局部损伤很敏感[ 16-17],对结构损伤大小的识别就可以转化为通过建立各损伤单元的应变残差最小为优化目标的多目标优化问题进行求解[18]，即:

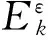
(20)

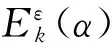
对于梁式结构损伤单元k的理论平均应变可表示为：

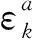
(21)

(22)

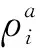
同理，损伤单元k的测量平均应变可表示为：

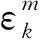
(23)

对式(20)进行求解，即可得到单元的刚度损伤系数α，从而实现对单元损伤程度的识别。

3 结 语

基于振动的应变类模态技术能对结构的损伤做出正确有效的识别，因而具有良好的应用前景，但对大型在役工程的实时在线损伤检测实际应用还处于探究阶段，必须进行进一步的深入研究，具体内容如下：①对噪声影响的研究。应在测试数据的过程中寻找更有效的降噪技术,从信噪分离上着手提高测量的精度；此外，应通过寻找更为敏感的识别因子来降低噪声对识别的影响以提高识别精度。②传感器的优化布置。大型复杂结构的自由度巨大且有些部位难以量测,给测试的工作量以及测试效果带来很大不利。传感器类型、数目及位置的选择要遵循功能要求和效益-成本分析两大原则，以获得最佳的信息组合。利用分布式光纤应变计以及采用遗传算法进行传感器的优化布设是一个新研究途径。③识别方法的研究。对大型的复杂结构可以通过实时监测系统进行损伤前后的对比监测研究而获得损伤前后的应变模态等相关参数，对于中小型结构进行在线监测则不太现实，从而很难获得损伤前的应变模态等信息，因此，寻找一种不需要损伤前信息的方法是实现对实际结构进行损伤识别的有效途径。

[1]李德葆, 陆秋海. 实验模态分析及其应用[M]. 北京:科学出版社, 2001.

[2]Yam L H,Leung T P, Li D B,et al. Theoretical and experimental study of modal strain analysis[J],Sound & Vibration,1996,192(2):251-260.

[3]孙建刚,郭巍.基于应变模态变化率的弯曲薄板结构损伤研究[J].哈尔滨工业大学学报，2007，39(8)： 1319-1322.

[4]任权,李洪升,郭杏林.基于应变模态变化率的压力管道无损检测[J].大连理工大学学报，2001，41(6)： 648-652.

[5]董聪，丁辉，高嵩.结构损伤识别和定位的基本原理与方法研究[J] .中国铁道科学，1999，20(3)：89-94.

[6]顾培英，邓昌，吴福生.结构模态分析及其损伤诊断[M].南京：东南大学出版社，2008.

[7]顾培英. 基于应变模态技术的结构损伤诊断直接指标法研究[D].南京：河海大学，2006.

[8]李智荣.压力管道腐蚀灾变检测应变敏度比法[D].大连：大连理工大学，2007.

[9]滕海文,霍达,姜雪峰，等.结构损伤位置识别的组合指标法[J].北京工业大学学报，2007，33(5):493-497.

[10]刘文峰，柳春图.利用广义应变比能进行结构损伤识别的数值研究[J].机械强度，2003,25(2)：159-162.

[11] Chen Xiaozhen, Zhu Hongping, Chen chuanyao. Structural damage identification using test static date based on grey system theory[J].Journal of Zhejiang University: Science, 2005, 6 A(8):790-796.

[12]基于曲率模态相关性的桥梁结构损伤识别研究[D].西安：长安大学，2008.

[13]邓聚龙.灰色系统基本方法[M].武汉：华中理工大学出版社，2005.

[14]陈孝珍，朱宏平，陈传尧.灰色相关性分析在结构静力损伤识别中的应用[J].力学与实践，2005,27(3)：60-64.

[15]瞿伟廉,陈伟,李秋胜.基于神经网络技术的复杂框架结构节点损伤的两步诊断法[J].土木工程学报,2003,36(5)：37-45.

[16]Pandey A K ,Biswas M ,Samman M M. Damage detection from changes in curvature mode shapes[J]. Journal of Sound and Vibration,1991,145(2):321-332.

[17]Abdel Wahab M M , De Roeck G.Damage detection in bridges using modal curvatures: application to a real damage scenario[J]. Journal of Sound and Vibration,1999,226(2):217-235.

[18]朱宏平.结构损伤检测的智能方法[M].北京：人民交通出版社，2009.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.08.034

TU311.3

A

1673-1409(2011)08-0109-05