冷连轧机主传动剪式安全销的弹塑性数值分析

闫成琨，黄 煜，王大号

(中国重型机械研究院有限公司，陕西 西安 710032)

1 前言

剪销式安全联轴器由于结构简单，造价低，在一些矿山机械、起重运输设备上常被用作过载保护装置。它的工作原理是当传递扭矩过大时，联轴器上的安全销被剪断，使传动中断，从而保护传动系统中的重要零部件。许多从国外引进的轧制设备，以及中国重型机械研究院自主成套设计的五机架全连续式冷轧机组主传动部分均采用了这种装置作为必要的机械保护。

但是在设备的使用过程中，包括从国外引进的设备，都出现了安全销大量非正常断裂的情况，使厂家的生产效率大大降低。这是由于剪式安全销的工作特性，既要保证安全销不会在正常工况条件下被剪断，又要保证其在非正常过载的情况下及时地被剪断，传统的机械设计手段很难准确把握。实际生产中，厂家大都是自行逐步增加安全销的抗剪强度或个数，直到不再断裂为止。这不仅增加了生产成本，也给设备安全带来许多不确定性。我院在对冷连轧主传动的剪销式安全联轴器设计时，虽然充分参考了国外的设计经验和不足，预先准备了多种规格的安全销和配置方案，但是在调试过程中仍然出现了安全销非正常剪断的现象。本文利用已经比较成熟的有限单元法，对在冷连轧调试过程中安全销的不同工况进行了弹塑性应力应变分析，并对今后的设计提出了一些改进意见。

2 剪销式安全联轴器及安全销结构

我院的冷连轧主传动剪销式安全联轴器配备了四种不同规格的安全销，安全销规格是按照安全销腰部最细部分的直径为准，有Φ11 mm，Φ12 mm，Φ13 mm，Φ14 mm等。在实际的生产过程中，根据主轧机不同的工况，可以选择使用不同规格的安全销。安全联轴器预留有12个销孔，正常生产时一般只安装2－4个。如果必要，在调试过程中可以适当增加安全销的数目。冷连轧机组使用的安全销如图1所示。

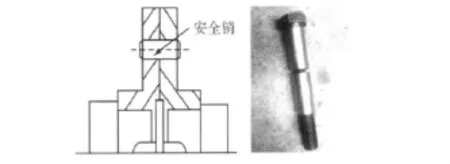
图1 安全销及其安装位置示意图Fig.1 Shear pin and its mounting position

3 有限元数值分析模型

3.1 力学模型

本机组主轧机上下工作辊独立传动，每个工作辊均为两台直流电动机串联输入。在电机和齿轮变速箱之间，配置有剪销式安全联轴器。为了方便进行数值分析，需要计算出单个安全销的受力情况并作合理简化。

计算电机的输出扭矩可以根据公式

式中，Me为电机额定扭矩，Nm，P为电机功率，kW，N电机额定电压转速，r/min。

单台电机的基本参数为:功率P=1 000 kW，额定电压转速N=270 r/min。可以得到两台电机串联布置输出的最大扭矩Me=70 740 Nm。

根据联轴器的安全销分布(图2)，由于分布圆直径是安全销腰部直径的40－50倍，因而可以忽略安全销在其分布圆内外侧受力大小的差异和对安全销的扭转效应，将作用在安全销上的受力看作是纯剪力分布，其合力为Fe，可以由电机额定扭矩，通过下式计算得出:

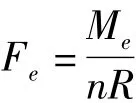
式中，R为安全销在安全联轴器上的分布圆半径，n为安装安全销的数量。本机组所使用的安全联轴器预留了12个销孔，即n最大可以取到12。实际生产当中，一般取n=2或4。本机组设计中初步选用4个安全销，即n=4。安全销的分布圆半径R=0.275 m，可得Fe=64 310 N。

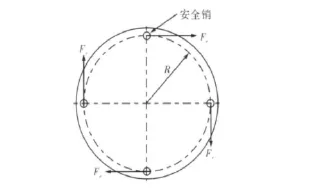
图2 安全销的分布和受力简化Fig.2 Load distribution and stress simplification of shear pin

考虑到Fe只是安全销腰部的内部剪力，并不是直接作用在安全销上的力，就要对分析对象进行受力分析，得出其力边界条件。直接作用在安全销上的力是有一定斜率的分布式载荷(图3)，但是考查重点是安全销的腰部破坏情况，可以将受力简化为图4中所示。这样也可以保证安全销腰部的受力情况与真实情况一致。

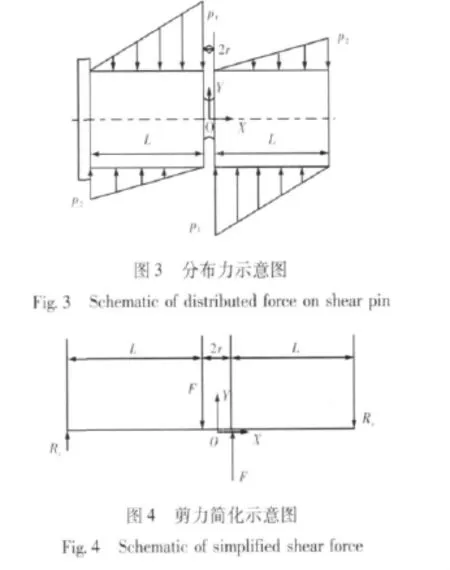
根据安全销的工作状况，其位移边界条件可以简化为两端简支梁，根据力和弯矩平衡条件，这样就可以计算出安全销的剪力和弯矩，

∑Y=0，即Ry－F+Fe=0

对于弯矩中心O点，

∑M=0，即－Ry×(L+r)+F×r=0

在本机组初选设计中，安全销的尺寸L=60 mm，r=2.5 mm，代入上两式，可以求得。

安全销在销轴弧面的分布力，对弧度方向积分，可以得到分布力p和端部载荷F的关系为

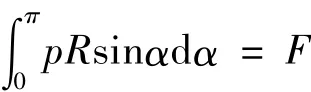
本文分析的安全销半径R=14 mm，可得p=2 393 000 N/m。

由此，安全销的力边界条件和位移边界条件均已知。

3.2 材料的弹塑性本构关系

本机组设计所用安全销的材料为45钢，其单向拉伸σ－ε曲线如图5所示

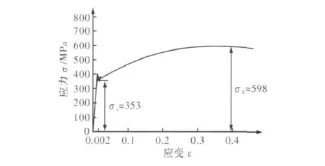
图5 45钢单向拉伸曲线Fig.5 Uniaxial tension curve of 45#steel

除了材料的基本σ－ε曲线，一般而言，弹塑性数值分析还必须依据三个基本准则来对材料进行判断。这三个基本准则分别为屈服准则，流动准则，硬化准则。

以屈服面理论为基础，常用的屈服条件有Tresca屈服条件和von Mises屈服条件。两者在屈服面上的投影轨迹如图6所示。从中可以看出，Tresca屈服条件在棱边处(或屈服轨迹在六边形的角点处)导数不存在，而von Mises屈服条件处处连续可导，因而在数值计算的处理上von Mises屈服条件更加方便。另外，大量实验结果表明，von Mises屈服条件比Tresca屈服条件大多数情况下更接近塑性材料的真实屈服情况。安全销的材料为45钢，von Mises屈服条件也更为适用。故本文在有限元计算中的屈服条件也以von Mises屈服条件为准。

流动准则规定了塑性应变增量的分量和应力分量以及应力增量分量之间的关系。von Mises流动准则，其向量方向沿应力空间内后继屈服面的法线方向。

硬化准则规定了材料进入塑性变形后的后继屈服函数。在有限元分析的当中，随动强化准则一般用于小应变分析，各向同性硬化准则适用于大应变的情况。对于本文所分析的对象而言，由于可能出现的大应变破坏情况，采用了各项同性硬化准则作为基本准则。

由前分析可知，安全销的材料模型可以使用多线性率不相关型各向同性强化模型，并依据图5对其单向拉伸σ－ε曲线建立近似的材料数据模型。

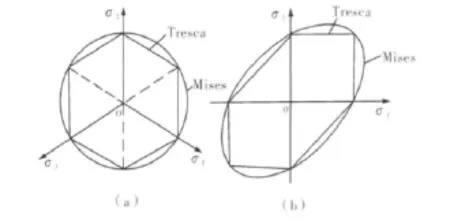
图6 Tresca屈服条件和von Mises屈服条件的投影轨迹Fig.6 Projection trace of Tresca and von Mises yield criterions

3.3 有限元计算

由于设备调试现场针对许多不同工况，进行了许多安全销配置方案的尝试。对每一种情况逐一建立模型进行分析既不现实也没必要。本文只选择了其中具有代表性的工况进行了分析。

现场调试过程中，按照最初的4个安全销配置方案，使用最大规格的安全销(Φ14 mm)，1#—5#机架的安全销几乎全部发生了非正常剪断的情况，故本文选择对4个Φ14 mm安全销配置方案进行有限元分析。

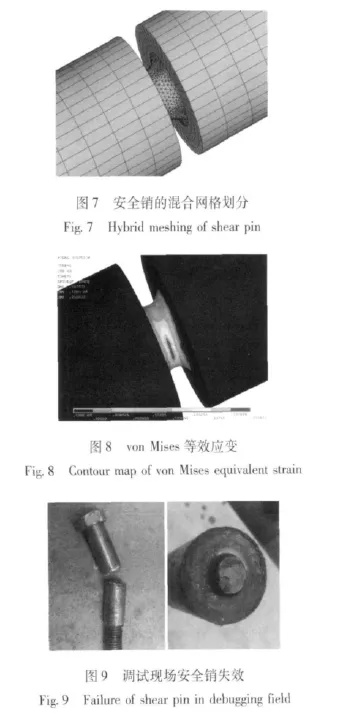
对Φ14 mm安全销建立三维实体模型。由于安全销的腰部的不规则性，需要使用四面体网格划分，同时为了保证精度，使用了10节点四面体单元。其余规则部分使用六面体网格来保证均匀性和计算精度，使用了20节点六面体单元。在两种单元的结合部分，使用了六面体单元和四面体单元的结合技术。网格划分结果如图7。

按照前节计算得出的力边界条件和位移边界条件施加载荷，计算结果以von Mises等效应变云图显示，如图8所示。

由分析结果可见，最大等效应变已经超过25%，说明安全销已经处于失效状态。这与实际使用情况一致。现场被剪断的安全销如图9所示。

在之后的调试过程中，尝试成对地增加Φ14 mm安全销的数量，最后使用到10个安全销时，安全联轴器不再出现非正常剪断的现象，主轧机工作正常化，轧制过程平稳可靠。因而，本文计算了10个Φ14 mm安全销同时工作在电机额定扭矩情况下的受力情况，计算结果如图10～图13。

图10 von Mises等效应力Fig.10 Contour map of von Mises equivalent strain

由计算结果的应力云图(图10、图11)可知，von Mises等效应力最大为360 MPa，剪应力最大为210 MPa，均在材料的许用工作范围内。应变云图(图12、图13)分析可知，von Mises等效应变不超过0.2%，接近于工程上约定的弹塑性分界点，von Mises等效塑性应变不超过0.003%，说明此工况下的安全销已经有微小的区域进入塑性状态。但是此时的安全销绝大部分材料尚处于弹性状态，仍然可以承受正常的工作载荷。这与现场实际调试的结果非常吻合。但是需要指出的是，此时的安全销并非是合理的工作状态，只是在一定的时间内、正常的轧制工况下保持有效。

4 分析与讨论

本文利用数值分析的手段，对冷连轧主传动剪式安全销进行了不同配置下的分析，得到了与生产现场使用情况相吻合的结论。

需要指出的是，本文所分析的安全销实际上并未处于合理的工作状态。这主要出于以下原因:

(1)由于实际轧制过程中，有时需要轧机短时间内处于一定程度的过载状态，一般是电机额定转矩的1.25倍以内，此时安全联轴器最好不会剪断失效。本文所分析的第二种情况下，安全销已经处于发生微小塑性变形的状态，不能够承受125%的过载，没有处于合理的工作状态;

(2)由于轧机在停机后需要重新穿带，会经常出现轧机反方向转动的情况，使安全销承受一定频率的交变载荷，通常是低周疲劳载荷。这会大大降低安全销的使用寿命，有时会导致正常载荷下也突然失效，影响生产效率。这也是目前的安全销设计中尚未考虑的疲劳问题。本文分析的安全销就是处于这种临界状态之下，从疲劳分析的角度看，也不是很合理;

(3)过多的安全销数量会降低其工作的可靠性。由于安全销的目的是为了保护传动系统，因而在意外大幅过载的情况需要其非常可靠地被剪断。而过多的数量实际上是降低了其工作的可靠度，使其在需要剪断的时候没有被剪断的概率大大增加了。实际上，如果一味增加安全销腰部的尺寸，在某种程度上也相当于增加了安全销的数量，降低了安全销工作的可靠度。

基于以上原因，在新的安全销设计中，应该从改变材料性能的角度入手，选择具有较高屈服极限和强度极限的材料，利用有限元分析的手段对其进行评估和优化，才能在保证其工作性能的前提下，提高其工作的可靠度。

［1］ 王仁，熊祝华，黄文彬．塑性力学基础［M］．北京:科学出版社，1982．

［2］ 黄克智，黄永刚．固体本构关系［M］．北京:清华大学出版社，1999．

［3］ 王勖成，邵敏．有限单元法基本原理和数值方法［M］．北京:清华大学出版社，1997．

［4］ 李友荣，贺文涛，刘安中．轧机主传动安全销弹塑性有限元分析［J］．重型机械，2005(5):45－48．

［5］ 王亮申．安全销联轴器的可靠性计算［J］．机械科学与技术，1998，(5):739－740．