冷轧机AGC控制系统模型研究

王 斌，寇 鹏，窦 锋

(中国重型机械研究院有限公司，陕西 西安 710032)

1 前言

近年来，随着汽车、家电产业的高速发展，对板带质量的要求越来越高，因此对轧机液压AGC控制系统的要求也越来越高。运用轧制基本理论和机电液控制技术，分析液压AGC系统的特点，提出优化设计和最优控制的思想，建立系统数学模型，这对于研究轧制过程中各种因素对质量的影响、了解轧机系统本身的固有特性、优化系统控制策略等具有重要意义。

2 液压AGC系统

液压AGC系统的控制对象是油缸，油缸通过电液伺服阀驱动。它的任务是接收电液伺服系统AGC系统的指令值，进行压下缸的位置或压力闭环控制，使压下缸实时准确的定位在指令所要求的位置或压力值，达到设定辊缝或压力的目的。

如图1所示，缸体相对于活塞的位移通过位移传感器检测出来，在实际系统中，为了消除活塞相对于缸体摆动的误差，位移传感器内置于缸体内，传感器分别固定于缸体和与活塞连接的挡板上。位移传感器检测出来的位置信号送到位置实时值输入端，与给定的设定值进行比较，得到的差值送至位置控制器进行调节，并经过伺服放大器进行放大后转换成电流信号送给电液伺服阀，系统中的电液伺服阀直接安装在压下缸上，伺服阀获得电流信号后输出负载流量给压下缸，压下缸就输出一定的位移，直到位移传感器的实测值与设定值相等为止，这就是液压AGC系统的闭环控制的过程。

图1 液压APC系统原理图Fig.1 Schematic diagram of hydraulic APC system

3 AGC控制中的主要模型

AGC控制系统中的模型有若干个，本文主要从以下五个方面进行说明。

3.1 位置控制器

位置控制器主要采用PI控制器，其动态传递函数为

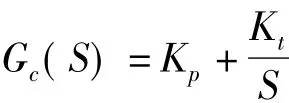
式中，Kp为比例系数;Kt为积分系数。

3.2 伺服放大器

伺服放大器的频宽比电液伺服阀的频宽高得多，响应速度很快，可不计时间常数，故可看做比例环节，其动态传递函数为

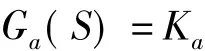
式中，Ka为伺服放大器的增益。

3.3 位移传感器

位移传感器可视为惯性环节

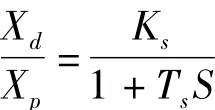
式中，Ks为位移反馈系数;Ts为位移传感器时间常数。

3.4 压力传感器

压力传感器可视为惯性环节

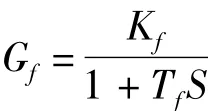
式中，Kf为压力反馈系数，Tf为压力传感器时间常数。

3.5 控制调节器

式中，Kp为PID调节器的比例系数;Ti为PID调节器的积分时间常数;Td为PID调节器的微分时间常数。

4 AGC系统控制模型

基本AGC系统由前馈AGC、监控AGC等联调所组成。通过AGC系统的控制，使来料厚度偏差得以消除，以保证成品带钢的厚度精度。如图2所示。

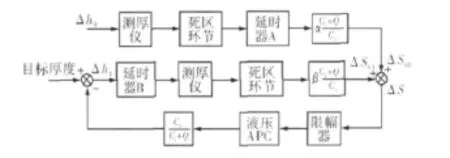
图2 前馈及监控控制模型结构图Fig.2 Structural diagram of feedforward and monitoring control model

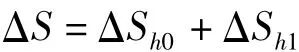
式中，ΔSh0为前馈AGC输出量，当来料厚差为监控AGC输出量，当出口厚差为Δh1时，ΔSh1

模型结构图中各个环节的数学模型分析如下:

(1)测厚仪环节。测厚仪的信号需要一定的时间处理，所以将对所检测的参数造成滞后，故可用一阶惯性环节来表示为

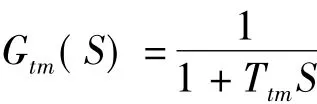
式中，Ttm为测厚仪的时间常数。

(2)延时器环节。带钢从入口测厚仪监测点移动到轧辊中心线需要一段时间，其传递函数可以用延迟环节表示为

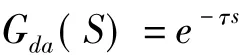
式中，τ为带钢移送延迟时间，τ=l0/v0，l0为机架前测厚仪与辊缝之间的距离;v0为带钢入口运行速度。

除了入口测厚仪测量点到辊缝需要一定时间，同时还要考虑测厚仪和液压压下执行机构也需要一定的响应时间，使得带钢的测量点在进入轧辊时，辊缝正好调整完毕，这样才能消除该厚差。前馈控制延时器B的传递函数可以用延迟环节表示为

式中，τ为带钢移送延迟时间，τ=L0/V0－τm;τm为测厚仪和液压压下的响应时间。

带钢从轧辊出来后移动到出口测厚仪的监测点也需要一段时间，即监控控制的纯滞后时间。该纯滞后时间特性由延时器C实现，可以用延时环节来表示为

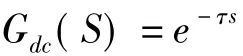
式中，τ为带钢移送滞后时间;τ=l1/v1;l1为轧辊辊缝与出口测厚仪之间的距离;v1为带钢出口运行速度。

(3)死区环节。设置厚差死区环节的目的是在保证控制精度的前提下，避免液压压下频繁动作，防止压下执行机构产生不必要或误动作，造成系统不稳定，起到保护压下设备和滤波的双重作用。死区输出按以下算法。

式中，Δh0为测厚仪的输出信号;d为死区域值;Δhx为死区环节输出信号。

(4)限幅器环节。设置限幅器环节是为了保证液压AGC的输出不大于最大值，避免辊缝调节量过大而影响带材的平直度，实际上是考虑了液压压下对板型的影响。限幅器按以下算法。

式中，ΔS为限幅器的输入信号;ΔSmax为限幅器的限定幅值，即允许的单机架最大辊缝调节量;ΔS1为限幅器环节的输出信号。

5 结束语

本文从液压轧机控制系统的原理为出发点，面向对象建立轧制模型。根据液压AGC系统的组成、各部件的动态环节和常用的控制方式，建立综合的参数化控制模型，基于这种模型，在多套轧机控制系统上成功应用，是较全面且利于分析轧制过程中各种因数对带材精度的影响的模型。

［1］ 刘长年．液压伺服系统的分析与设计［M］．北京:科学出版社，1985．

［2］ 连家创，刘宏民．板厚板型控制［M］．北京:兵器工业出版社，1996．