薄板轧制力的研究与模拟分析
2011-11-18杨福亮李玉贵
杨福亮 李玉贵 范 飞
(太原科技大学,山西 030024)
在板带轧制中,轧制力的快速准确预报对改善板材质量、提高成材率具有重要意义。板带轧制是一个非线性、多变量耦合且存在时变的复杂过程,建立精确的解析模型十分困难。如某板带冷轧厂使用的由国外某公司提供的轧制力模型的设定值与实测值之间相差较大,有时高达17%以上[1],对现场生产造成了较大影响。为了获取一个相对较高精度的轧制力模型,本文在综合考虑轧辊弹性变形与轧件的弹塑性变形的基础上,建立了一个相对计算精度较高的轧制力计算模型,并采用数值迭代法对轧制力进行了推导分析,最后运用有限元模拟软件ANSYS 对轧制过程进行了模拟分析,从而验证了此计算公式的正确性。通过计算结果与模拟分析结果的数据对照,表明该模型较文献[1]所述情况有明显的改善,更能满足薄板冷轧生产轧制力预算所需的精度要求。
1 轧制力模型的理论推导
冷轧时,带钢不仅会发生塑性变形,而且在入口和出口处还存在弹性变形,因此,可将轧制过程中的轧件分为弹性变形区和塑性变形区两部分进行轧制力的计算。图1 是薄板冷轧过程中轧件所受轧制力分布曲线与对应的弹塑性变形之间的示意图[2]。
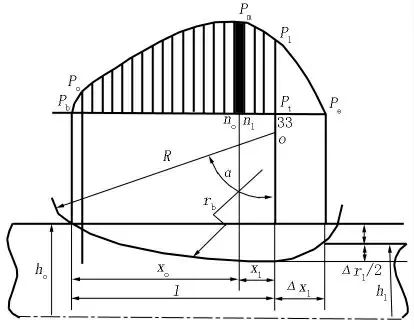
图1 单位压力分布曲线和对应的弹塑性变形区示意图Figure 1 Schematic drawing of pressure distribution curve per unit and corresponding elastic-plastic deformation area
Bland-Ford-Hill 轧制力模型考虑了弹性变形和塑性变形这两种状态,因而成为带钢冷轧最常用的轧制力计算公式[3]:

式中 F 为总轧制力,kN;
Fp为塑性区轧制力,kN;
Fe为弹性区轧制力,kN。
QF为应力状态系数;
km为变形抗力,MPa;
R'为轧辊压扁半径,mm;
B 为带钢宽度,mm;
v 为泊松比;
E 为杨氏模量;
ξ 为张力影响系数。
由以上3 个公式可以看出,要想求出总轧制力必须要解决R'、QF、km、ξ 等几个量的问题。
2 轧制力公式中主要参数的确定
2.1 变形抗力km
金属变形抗力km是指单向应力状态下,金属材料单位面积上产生塑性变形所需力的大小。它的大小取决于金属材料的化学成分以及塑性变形时的物理条件(变形温度,变形程度,变形速度等)。变形抗力是轧制力模型中一个极其重要的物理参数,它的计算精度直接影响轧制力模型的计算精度[4]。
在模型设定中,压力公式采用相应于各种钢种的变形抗力公式来计算。

N——轧机转速,r/min;
t——轧制温度,℃;
k0——基准变形阻力,MPa,即t=1 000℃,
e=0.4,μ=10s-1时的变形阻力;
a1~a6——回归系数。
k0,a1~a6见表1 所示。
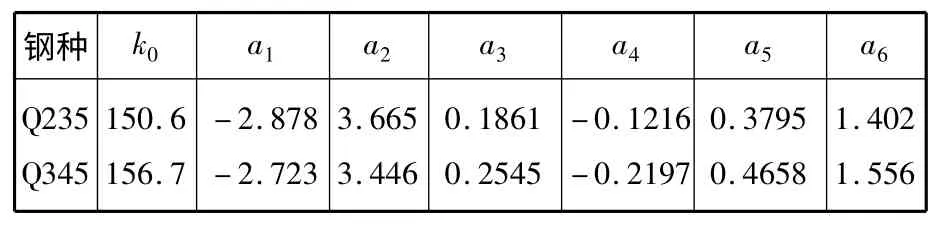
表1 钢种Q235 和Q345 变形抗力公式回归系数Table 1 The regression coefficient of deformation resistance formula for steel grade Q235 and Q345
2.2 张力影响系数
前后张力的施加均是轧制力降低,且呈近似线性关系。张力影响系数可表示为:

式中 a——系数,一般取值0.7;
Tb、Tf——为带钢入口、出口单位张力,MPa;
k——平面变形条件下材料的变形抗力,MPa。
2.3 应力状态系数QF
由文献[5]知希姆斯模型结构回归建立的压力模型较好的吻合了实际轧制力的变化,误差仅在0.581%~9.452%之间,模型精度较高,这里也选用这种模型,并做进一步改进。

f——摩擦系数。
2.4 轧辊压扁半径R'
由于轧辊表面受到轧制力的作用而产生压扁,使得接触弧长加大,轧制力也相应增大。对于冷轧薄板来说,轧辊及轧件弹性变形所引起的接触弧长的变化是不能忽略的,本文针对轧辊压扁半径采用经典Hitchcock 公式求解[6]。

式中 R0——轧辊初始半径;
Δh——带钢压下量。
由上式可以看出,在进行轧制力预算时,轧制力、应力状态系数与轧辊压扁半径等几项之间存在着不同的耦合关系,三者既可以由以上7 式组成方程组进行求解,也可以相互迭代进行求解。

3 轧制力仿真实验
为了验证理论推导轧制力预算模型的正确性,选用钢种Q235 进行仿真实验,图2 为建立的轧制力仿真模型。
仿真以某实际可逆式四辊冷轧机为研究对象建模,单元类型选择solid164,辊颈设为刚体,辊身为弹性体,轧件为非弹性体。轧制过程采用分道次轧制,轧制过程分为5 个道次,各道次压下量、轧制力等情况在表2 详细列出。分析轧制过程某一时刻的轧件成型情况如图3 所示。

图2 轧制力仿真模型Figure 2 Simulation mode of rolling force
由图3 可以看出,板带成型过程可明显分为入口弹性变形区、塑性成型区和出口弹性变形区等3 部分,局部应力的最大值位于轧辊的平衡界面处,单位轧制力的分布与理论分析结果及传统经验分布结果相同,在一定程度上证明了仿真结果的正确性。
采集模拟轧制过程中的轧制力数据如图4 所示。

图3 Q235 仿真轧制过程中单位轧制力分布示意图Figure 3 Schematic drawing of rolling force distribution per unit during simulation rolling of Q235

图4 模拟轧制过程采集轧制力数据Figure 4 Rolling force data collected during simulation rolling
由于仿真过程中轧件被划分为若干网格,由计算机计算出的轧制力曲线变成一条不断震荡的曲线。随机选取轧件上10 个点位的轧制力值,并算取平均值作为仿真过程中的轧制力值。
4 轧制力模型计算结果与仿真结果比较
按照仿真过程的多道次轧制方案利用式(8)给出的轧制力预算公式进行计算,得到各道次的轧制力值。Q235 轧制力计算值与仿真值比较如表2 所示。
通过计算值和仿真值的比较(见图5)可以看出,计算值与仿真值的误差在 范围内,较之文献[1]提到的误差度有明显的改善。本文建立的轧制力预控模型精度较高,且稳定性好,能够满足薄板冷轧生产轧制力预算所需的精度要求。

表2 Q235 轧制力计算值与仿真值比较Table 2 The comparison of calculation value with simulation value for rolling force of Q235
5 结论

图5 Q235 轧制力计算值与仿真值Figure 5 Calculation value and simulation value of Q235 rolling force
本文根据薄板轧制的实际情况,综合考虑轧辊弹性压扁、张力和摩擦状态等因素对轧制力模型的影响,建立了薄板冷轧过程中的轧制力预控模型。通过与有限元模拟结果的对比,验证了模型的合理性与正确性,并结合实际计算过程中的经验得出了以下结论:
(1)薄板轧制过程中进行轧制力预算时,由于轧件很薄,轧件的弹性变形在整个变形中占的比例较大,所以弹性变形区对轧制力的影响不能忽略,否则会严重影响计算结果,使计算结果与实际值相差增大。
(2)用本文方法建立的薄板冷轧轧制力预控模型精度较高,能够满足冷连轧实际生产的要求。
(3)利用ANSYS 软件进行变形仿真分析,能够准确地施加各种初始条件和边界条件,可以获得较全面的应力应变信息,是一种经济有效的研究方法。
[1]张清东,徐兴刚,于孟,瞿标,李实.基于遗传神经网络的不锈钢带冷轧轧制力模型[J].钢铁.2008.43(12):46-49.
[2]刘兴刚,谭树彬,崔建江,徐心和.冷连轧第5 机架轧制力模型.东北大学学报(自然科学版).2004.25(1):5-8.
[3]白金兰.王军生,王国栋,等.提高冷轧过程控制轧制力模型的设定精度[J].钢铁研究学报.2006.18(3):21-25.
[4]周纪华.金属塑性变形阻力[M].北京:机械工业出版社,1989.
[5]张毅,张华,程晓茹,等.中厚板轧制力数学模型的研究[J].钢铁研究.2005.8(4):18-21.
[6]V.B.金兹伯格.板带轧制工艺学[M].北京:冶金工业出版社,1998.
