动态回归模型在变形分析中的应用*
2011-11-14邓兴升陈石桥殷自成
邓兴升 陈石桥 殷自成
(1)长沙理工大学测绘工程系,长沙 410004 2)湖南省电力公司柘溪水电厂,安化413508)
动态回归模型在变形分析中的应用*
邓兴升1)陈石桥2)殷自成1)
(1)长沙理工大学测绘工程系,长沙 410004 2)湖南省电力公司柘溪水电厂,安化413508)
为了使回归模型适应动态数据集,推导了动态回归模型的递推最小二乘算法,数据更新时,采用修正方式更新回归系数计算两个矩阵,避免了重复矩阵求逆运算,实现了观测数据增加而矩阵阶数不增加,理论上减少了计算时间。以柘溪和东江两大坝变形分析多元动态回归模型为例进行实验,结果表明:该方法建模过程简洁、无需迭代计算,易于编程实现,在计算效率与预报精度等方面均具优势,可应用于实时变形分析建模。
动态回归模型;递推最小二乘算法;数据更新;动态数据集;变形分析
1 引言
为了揭示变形与环境因素的关系,人们研究了许多变形监测模型[1-6],这些方法适用范围不同,各有其优点,但无论何种模型都较为复杂,涉及迭代运算;且都不能提高观测数据固有的观测精度。对实时性高要求的大坝安全监测应用而言,分析模型的计算效率非常重要。多元线性回归分析模型是一种经典的实用于变形观测数据处理的数理统计方法,模型参数计算无需迭代与随机搜索,易于编程实现,因而具有简洁易用的特点。但回归模型自建立后便有其生命周期,随着观测数据的增加,回归模型可能不再适用而需要重新建立。为了提高模型参数的计算效率,本文推导了动态回归模型最小二乘递推算法,它是在已建立回归模型的基础上,通过模型修改实现模型参数的递推计算。
2 动态回归模型
2.1 多元线性回归模型

式中,Qe为残差平方和,为σ2的无偏估计,n为样本数,p为因子数。求得后则可以根据自变量和公式=计算因变量的预测值。

2.2 动态回归模型
在建立回归方程的过程中,对于动态数据集,当环境条件发生变化时,原先建立的回归方程就不可能反映这些新的信息,如继续使用它进行预测,势必导致预测精度降低和模型误差增大。解决这个问题的方法有两种:一是将新增加的观测数据同历史数据放在一起,重新建立回归方程,但这种作法计算量大,不便于应用;二是对回归方程的参数采取递推估计的办法,使它能随新观测数据的增加不断地修改回归方程的参数,以反映出最新环境的变化,这种方法计算量少,便于应用。
由于回归模型没有考虑动态数据集的建模问题,新增观测数据后,回归模型面临修改或重新建立。由于数据集的变化导致在模型计算过程中需要反复进行矩阵相乘、求逆,需要耗用较多计算时间,因此本文建立动态回归模型的最小二乘递推算法,当获得新增观测数据后,在对原有模型进行参数估计时,为了满足动态回归的需要,不需要重新建模求解,而是由最小二乘估计导出回归系数的递推最小二乘算法,使新的信息加入后可以直接修正原来的计算结果。这样可以简化计算量,避免费时的矩阵求逆运算,理论上提高了计算效率。
在初始回归模型的基础上,设新增观测数据为(Xa,Ya),ε为一设定的任意小值,它与具体的应用有关,如果

则认为现有模型对新观测数据是适应的,可以不对模型进行修改。否则设:

则

随着新观测数据的增多,X1与Y1矩阵阶数逐渐增大,直接根据式(4)进行新的模型参数计算需要进行矩阵求逆,反复计算,效率较低,难以适应于动态数据集及实时建模领域。因此本文提出了以下不增加矩阵阶数,且避免矩阵求逆的动态回归算法。
在式(1)中,设


根据矩阵反演公式(D+ACB)-1=D-1-D-1A (C-1+BD-1A)-1BD-1,其中A、B为任意矩阵,C、 D为任意可逆矩阵。结合式(5)、(6)有:
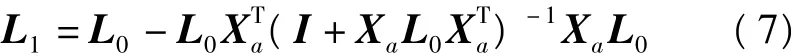
在式(7)中,XaL0的结果为1×1阶矩阵,即为一个数,单位矩阵I为1,设

则有,

由公式(9)可见,只需要根据初始回归模型中的逆L0和新增数据Xa就可以得到动态回归模型的逆L1,且不涉及求逆运算。
结合公式(5),有

由公式(10)可见,根据新增观测数据(Xa,Ya)和初始回归模型的W0,可求得动态模型的W1。
则动态回归模型的系数矩阵为:


动态回归模型参数的解,仍遵守最小二乘准则,由式(8)~(12)计算,避免了矩阵求逆,充分利用原回归模型的计算结果L0和W0进行递推计算,计算过程中矩阵阶数不增加,L0为p+1阶方阵,W0为(p+1)×1阶矩阵;新增观测数据(Xa,Ya),其中Xa为1×(p+1)阶矩阵,Ya为1×1阶矩阵;p为常数,意义同公式(1)。历史数据不必存储,无论样本增加多少,该算法中的矩阵阶数始终不变,因此计算效率不随样本增加而下降。矩阵阶数与矩阵求逆运算时间呈正比,因此,对于高阶高维问题,本算法的优势更显著。而常规回归公式(4)需保存历史数据,并涉及矩阵阶数增加及矩阵求逆问题,因而随着观测数据增加,其计算效率将逐渐下降。
2.3 回归方程的显著性检验
1)提出原假设H0:线性关系不显著;
3)由显著性水平a,查F分布表,得到Fa(k,n -k-1);
4)若F>Fa,拒绝H0,即认为线性关系显著;否则接收H0,即认为线性关系不显著。
3 变形分析实例
以柘溪大坝和东江大坝水平位移建立动态回归模型,对比测试计算时间与效率;在不同因子组合模式下,测试模型预报精度、相关系数、模型修正次数。在表1、2中,R代表相关系数;MAPE代表预报平均绝对百分比误差;MSE代表预报均方根误差,单位为mm;MAE代表预报平均绝对误差,单位为mm; TN代表模型修正次数。
3.1 柘溪大坝
柘溪大坝主要为单支墩大头坝及宽缝重力坝,大坝全长330 m,坝顶高174 m,最大坝高104 m。坝顶水平位移采用视准线法观测,视准线全长473 m,基准点设在两岸坚硬的基岩上,测点布设在坝顶下游栏杆外专用的牛腿上,距坝轴线15.40 m,由4号进水口至左重3号重力坝段,每个坝段设一个测点,共17个测点。采用Wild T3经纬仪和专用的固定和活动觇标施测。1968年5月开始观测,每月观测1次,至今已获得550期观测数据。该视准线距附近建筑物较近,全长超过300 m,观测误差达3 mm左右,超出《DLT5178-2003混凝土大坝安全监测技术规范》要求。
先对柘溪大坝坝顶水平位移进行建模分析。由250周期观测值建立初始回归模型;然后采用2.2中的方法,每增加一周期观测数据判断公式(2)(ε取0.9 mm)的条件是否满足,如果不满足,则根据公式(8)~(12)建立动态回归模型,对300周期的观测位移进行预报,若每次采用回归模型直接求解,计算时间为0.46 s;若采用动态回归模型,计算时间为0.41 s,计算效率提高了12.2%。水平位移观测值和模型预报值之间的对比见图1,预报误差见图2。不同因子组合条件下模型各指标见表1。
图1~2及表1显示,32%的预报误差大于2 mm,MSE为1.957 8 mm(偏大)。采用全部因子建模时,相关系数为0.706 3,表明位移预报值与观测值之间吻合欠佳,其主要原因是在于视准线较长,受大气折光、活动觇标隙动差等因素的影响,导致视准线的观测精度偏低。从不同因子组合模式下的测试结果可知,影响柘溪大坝水平位移的主要因子是温度和水位组合,其中温度因子占的权重更大,而时效因子的影响较小。
显著性F检验时,F值为32.97,显著性水平a设为0.005,查F分布临界值表得Fa(10,289)为2.55,F大于Fa,故认为回归方程线性关系显著。

图1 柘溪大坝水平位移观测值与预报值过程曲线Fig.1 Curves of Zhexi dam deformation observations and predicted values

图2 柘溪大坝水平位移预报误差Fig.2 Dynamic prediction errors of deformation of Zhexi dam

表1 不同因子组合条件下的模型指标Tab.1 Model indexes under different factor combinations for the Zhexi dam
3.2 东江大坝
东江大坝为混凝土双曲拱坝。本例取自垂线观测项目,观测点为250 m高程L5号垂线径向位移,已有观测数据293周期,以其中前50周期建立初始模型;采用动态建模预报后243周期,取ε为0.9 mm。若每次采用回归模型直接求解,计算时间为0.44 s;若采用动态回归模型,计算时间为0.39 s,计算效率提高12.8%。水平位移观测值和模型预报值之间的对比见图3,预报误差见图4,不同因子组合条件下模型各指标见表2。

图3 东江大坝水平位移观测值与预报值过程曲线Fig.3 Curves of Dongjiang dam deformation observations and predicted values

图4 东江大坝水平位移预报误差Fig.4 Dynamic prediction errorsofdeformation of Dongjiang dam

表2 不同因子组合条件下模型各指标Tab.2 Model Indexes under different factor combinations for the Dongjiang dam
由图3~4及表2可知,位移预报值与观测值之间吻合很好,67%的预报误差小于1 mm,反映了东江大坝垂线观测精度较高;另一方面表明了东江坝体水平位移与库水位、气温、时效等因素有密切的相关性,位移观测值与模型预报值之间的相关系数为0.986 3,两者的一致性非常好。模型预报MSE误差值为0.963 3 mm,低于大坝监测规范要求的1 mm,模型预报精度指标整体上优于柘溪大坝的预报结果。从不同因子组合模式下的测试结果可知,影响东江拱坝水平位移的主要因子是温度和水位组合,其中温度权重比较显著,而时效因子的贡献较小。
显著性F检验时,F值为748.14,显著性水平a设为0.005,查F分布临界值表得Fa(10,232)为2.55,F远远大于Fa,故认为回归方程线性关系显著。
4 结语
两个实例表明,只需要获得少量观测数据就可以建立初始回归模型,并根据新增观测数据逐渐建立动态回归模型,使模型始终保持最优的预测性能。动态回归递推算法具有线性、简洁、易于编程实现、无需迭代与随机搜索的优点。实例中提高计算效率12%,在计算时间与精度等方面都具有一定优势,对于高阶高维问题,算法的优势更显著,可适用于动态数据集的实时回归建模。
1 王新洲,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报(信息科学版),2008,33(5):469 -471.(Wang Xinzhou,et al.Dam deformation prediction based on wavelet transform and support vector machine[J].Geomatics and Information Science of Wuhan University,2008,33(5):469-471)
2 王利,等.动态灰色预测模型在大坝变形监测及预报中的应用研究[J].西安科技大学学报,2005,25(3):328 -332.(Wang Li,et al.Application of dynamic gray forecast model in dam deformation monitoring and forecast[J].Journal of Xi’an University of Science and Technology,2005,25(3):328-332)
3 李捷斌,孔令杰.基于Kalman滤波的BP神经网络方法在大坝变形预测中的应用[J].大地测量与地球动力学,2009,(4):124-126.(Li Jiebin and Kong Lingjie.Application of BP neural network based on Kalman filtering to dam deformation prediction[J].Journal of Geodesy and Geodynamics,2009,(4):124-126)
4 刘福深,等.基于差异进化算法的前馈神经网络在大坝变形监测中的应用[J].岩土力学,2006,27(4):597-600.(Liu Fushen,et al.Application of feed-forward neural networks to dam deformation monitoring based on differential evolution algorithm[J].Rock and Soil Mechanics,2006,27(4):597-600)
5 赵二峰,等.基于递阶对角神经网络的大坝变形预报模型[J].武汉大学学报(工学版),2009,42(3):344-348.(Zhao Erfeng,et al.Dam deformation forecast model based on hierarchical diagonal neural network[J].Engineering Journal of Wuhan University,2009,42(3):344-348)
6 谈小龙,等.高边坡变形的组合预测模型及其应用[J].水利学报,2010,41(3):294-299.(Tan Xiaolong,et al.Hybrid prediction model for high slope displacement and its application[J].Journal of Hydraulic Engineering,2010,41 (3):294-299)
7 林志兴,梁飞豹.基于最小二乘法的递推回归[J].福州大学学报(自然科学版),2006,34(1):24-27.(Lin Zhixing and Liang Feibao.The recursive regression based on least square method[J].Journal of Fuzhou University(Natural Science),2006,34(1):24-27)
APPLICATION OF DYNAMIC REGGRESSION MODEL IN DEFORMATION ANALYSIS
Deng Xingsheng1),Chen Shiqiao2)and Yin Zhicheng1)
(1)Department of Surveying Engineering,Changsha University of Science&Technology,Changsha 410004 2)Hunan Electric Power Zhexi Hydro-electric Power Plant,Anhua413508)
The recursive least squares algorithm for dynamic regression model,which can be used in the online regression modeling for dynamic data sets,is deduced.When the new observations updating,the dynamic regression algorithm,by avoiding the increment of matrix size,and avoiding the computation of the inverter matrix,can decrease the computation time of solving model parameters.The algorithm is easy to be programmed and no iterative computation is needed.The simplicity and practicality have been verified by using the dynamic regression approach in Zhexi and Dongjiang Dam deformation prediction samples.By compared with other algorithms,the method can reduce computation time and improve prediction precision.
dynamic regression model;recursive least squares algorithm;data update;dynamic data sets;deformation analysis
1671-5942(2011)05-0132-05
2011-03-29
湖南省自然科学基金(10JJ3090)
邓兴升,男,1971年生,高级工程师,博士,主要从事统计学习理论及其在大地测量中应用方面的研究.E-mail:whudxs@ 163.com
P207
A
