重力时序变化系统稳定性的研究*
2011-11-14郭树松祝意青
郭树松 祝意青
(1)中国地震局第二监测中心,西安 710054 2)中国科学院测量与地球物理研究所动力大地测量学重点实验室,武汉430077)
重力时序变化系统稳定性的研究*
郭树松1)祝意青1,2)
(1)中国地震局第二监测中心,西安 710054 2)中国科学院测量与地球物理研究所动力大地测量学重点实验室,武汉430077)
把重力时序系统视为慢时变系统,根据线性系统分析的理论方法,用差分方程描述该系统的等价参数模型,通过判断参数序列的稳定性来探索前兆异常。对河西流动重力观测网1994—2009年3个测点的观测数据的计算分析验证了该方法的有效性,但失稳与地震前兆的关系还需进一步研究。
重力时序变化;慢时变系统;差分方程;参数序列;河西重力观测网
1 前言
地震前兆系统分析是当今科学研究领域的一大难题,对该系统而言,其结构机制与内部机理均不甚明了,无法通过动力系统的模型方法来探索其复杂特性和过程。研究表明,地震的孕育和发生过程伴随着由于断层构造活动和局部地壳应力集中而引起地壳形变(高程)和密度(质量)的变化,从而引起包括重力场在内的多种地球物理场的变化。流动重力测量反映了构造活动区重力场随时间的非潮汐变化,地壳内部的密度异常、质量迁移和地震的形成过程等都可在流动重力复测结果中反映出来[1,2]。因此,研究区域重力场的时空动态演化特征是探索地震前兆异常的一条重要途径。
目前对流动重力观测资料的研究方法可以分为两类,一类通过网格化对数据进行内插滤波,得出二维的重力场连续变化图像,从整体上分析测网内应力-应变场微动态活动;另一类分析特殊区域(一般为重力变化高梯度带和正、负异常变化的过渡区域)内测点或剖面重力的时序变化,时序变化能较好地突出异常动态,从而探索断裂的构造活动。在研究中一般把两者综合起来进行地震趋势预报[3,4]。但是,对许多地震来说不能直接得到重力变化的范围,地震也不是发生在重力变化的最大点上,短期重力变化的大小也可能包含着测量粗差及浅表局部干扰。针对这样的问题,本文探索一种判断重力时序变化稳定性的方法,把长期的时序变化看作一个慢时变系统,通过分析时序系统结构变化和稳定性的过程探索前兆异常。
2 理论模型
2.1 基本原理
流动重力观测网所构成的蕴震系统是一个非线性、非平衡的慢时变系统,其演变过程是一系列的离散数据。对于离散系统一般用差分方程建立参数模型,系统辨识就是确定这些参数。模型参数是对系统行为结构的描述,定常系统的结构不变,参数亦不变,时变系统的结构在改变,相应的参数亦改变。因此时变参数序列就反映了系统结构的改变,这是我们探索地震前兆的基础。
对于单输入单输出系统的动态过程可描述为[5]:

其中u(k)、y(k)分别为系统的输入、输出,a1(k)、…、an(k)为模型参数,n为系统的阶数,时变系统中参数是时间的函数。前兆系统的建模就是确定方程的阶数n,求出n个时变参数函数,即n个参数的序列值。
由线性理论分析得知,方程(1)的特征方程为

这是复平面Z上的方程,其根称为系统的闭环极点。闭环系统的动态性能与闭环极点在Z平面上的位置密切相关。参数变化时,特征方程的根在Z平面上运动的轨迹称为根轨迹。在自控工程设计中,正是利用闭环极点位置的改变来改善系统稳定性及其动态性能。而在前兆系统分析中,正好相反,是利用根轨迹来分析系统的失稳过程与地震前兆异常的关系。
2.2 建立模型
如图1所示,我们可以把输入函数g(t)合理地划分为若干个时段,每个时段的输入函数为u(k)。假定每个时段的输入函数可以用一个阶跃函数近似表示,例如u(k)=b(k)u(1),其中u(1)为单位阶跃函数,b(k)为该时段的跃度,是一个未知值。故式(1)可表示为

从式(3)可以看出,时变系统的输出中,既有输入的因素,又有参数变化的因素;也就是说,系统输出中也包含了输入的信息。因此,在求时变参数时,可同时求出该时段输入函数的跃度b(k)值。因此,式(3)就是我们采用的模型方程。
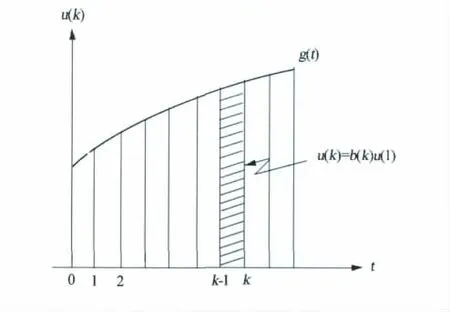
图1 输入函数的曲线模拟Fig.1 Simulation curve of input function
实际上,时变参数估计可采用实时递推估计法[6]的公式计算。该方法的递推公式为:

其中

式中,θT(N)是由输入、输出的模型参数组成的矩阵,对于递推初值(0)为任意值;P(0)=α2I,α为无限大,I为单位矩阵。λ为遗忘因子,取值在0到1之间,它对老数据不断进行截尾,从而使实时算法一直保持着对参数估计的校正能力。
这里需要注意的是确定参数的阶数n是建模成败的关键,遗忘因子λ取值的大小直接影响到对参数的跟踪能力。对每一个定点观测系统,二者都要经过反复试算比较才能确定最佳取值。
2.3 系统失稳判定
系统失稳判定是分析前兆异常的重点,首先要解决特征方程求根问题。在线性系统分析中,一般是将差分方程描述通过变量代换化为状态变量描述,与状态变量相乘的矩阵A称为系统矩阵。对单输入、单输出系统而言,矩阵A的特征值就是特征方程(2)的根。由此推导出矩阵A的组成为:


3 实例分析
北祁连河西流动观测网位于青藏高原东北缘(图2)。测网所在区域是中国大陆地壳运动最强烈、地震活动频度最高、强度最大的地区之一。从1989年开始中国地震局第二地形变监测中心在该地区初步建立了流动重力监测网,后经多次扩建和加密,形成目前的北祁连河西流动观测网。1989年开始在该地区每年进行一次重力测量(1993年停测1期,2009年开始每年观测2期),至今已有21期测量成果。各期观测精度都在12×10-8ms-2以上,观测精度较高,观测资料可靠。
我们选取该观测网中的134、57和28号测点(图2),用本文方法研究其重力时序变化的稳定性。1994—2009年该测段和测点的重力时序变化和时序系统矩阵根的模如图3~5所示。其中参数模型的阶数n=3,遗忘因子λ=0.95。


图2 河西地区重力观测网及构造分布Fig.2 Distribution of gravity survey network and tectonic diagram in Hexi area


4 结语
1)以上几个例子较好地反映了该方法对重力时序系统是否稳定的判断的正确性,大量计算也表明,虽然各测点所受的干扰因素不同,构造活动对每一个测点的影响方式不同,分析某一区域内各测点的时序稳定性也不尽相同,但多数测点所反映的总体稳定性趋势是一致的。
2)从数值分解的角度分析,我们通过建模将一列观测值分解为n+1个序列,和观测序列相比,引起每个参数变化的因素相对减少了,曲线中包含的成份简单了。但是,数学模型只是分析系统的工具,并不代表形成系统的机理。因此对系统结构稳定性的判断,仍然要从系统环境变化方面去推测,仍然要从分析参数曲线的正常基值线去理解。
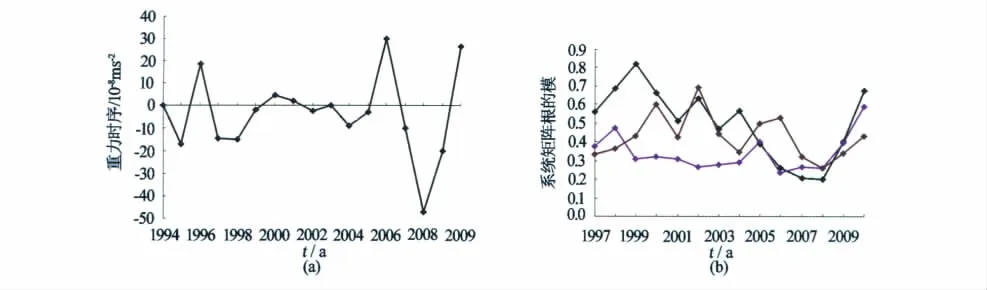
图3 134号测点1994—2009年的重力时序变化图(a)及其系统矩阵根的模(b)Fig.3 Gravity time-variation at 134 observation point from 1994 to 2009(a)and the modules of characteristic root of its coefficient matrix(b)

图4 57号测点1994—2009年的重力时序变化图(a)及其系统矩阵根的模(b)Fig.4 Gravity time-variation at 57 observation point from 1994 to 2009(a)and the modules of characteristic root of its coefficient matrix(b)

图5 28号测点1994—2009年的的重力时序变化图(a)及其系统矩阵根的模(b)Fig.5 Gravity time-variation at 28 observation point from 1994 to 2009(a)and the modules of characteristic root of its coefficient matrix(b)
3)本文只是初步研究,针对重力时序系统失稳要研究的问题很多,如失稳是否发生在最大的一个或两个特征值序列上,最大根植序列是否有迁移,失稳的形态是持续型还是振荡型,地震前兆异常的特征是什么…等,失稳并不都意味着地震前兆异常,这些问题还需要进行大量计算,结合构造活动尤其是震例在根轨迹图上仔细分析,才能最后确定。
1 祝意青,等.河西地区重力场及其动态演化特征[J].大地测量与地球动力学,2003,(4):44-48.(Zhu Yiqing,et al.Study on gravity field and its dynamic evolutional characteristics in Hexi area[J].Journal of Geodesy and Geodynamics,2003,(4):44-48)
2 祝意青.青藏高原东北缘强震前兆特征研究[J].国际地震动态,2007,(5):16-21.(Zhu Yiqing.Precursory characteristics of stronger earthquakes innortheastern edge of Qinghai-Tibet plateau by using mobile gravity technique[J].Recent Developments in World Seismology,2007,(5):16-21)
3 祝意青,等.龙门山断裂带重力变化与汶川8.0级地震关系研究[J].地球物理学报,2009,52(10):2 538-2 546. (Zhu Yiqing,et al.Relations between gravity variation of Longmenshan fault zone and Wenchuan Ms8.0 earthquake[J].Chinese Journal of Geophysics,2009,52(10):2 538 -2 546)
4 李辉,等.滇西地区重力场动态变化计算[J].地壳形变与地震,2000,20(1):60-66.(Li Hui,et al.Computation of dynamic gravity changes in Westen Yunnan[J].Crustal Deformation and Earthquake,2000,20(1):60-66)
5 夏德铃.自动控制理论[M].北京:机械工业出版社,2000.(Xia Deling.Automatic control theory[M].Bejing:China Machine Press,2000)
6 谢新民,丁锋.自适应控制系统[M].北京:清华大学出版社,2002.(Xie Xinmin and Ding Feng.Adaptive control system[M].Bejing:Qinghua University Press,2002)
7 祝意青,等.景泰5.9级地震前后的重力变化研究[J].中国地震,2001,17(4):356-363.(Zhu Yiqing,et al.Research on gravity variation before and after Jingtai Ms5.9 earthquake[J].Earthquake Researth,2001,17(4):356-363)
8 祝意青,等.民乐6.1、岷县5.2级地震前区域重力场变化研究[J].大地测量与地球动力学,2005,(1):24-29.(Zhu Yiqing,et al.Research on the variation of gravity field before Minle Ms6.1 and Minxian Ms5.2 earthquakes[J].Journal of Geodesy and Geodynamics,2005,(1):24-29)
9 王宏华.现代控制理论[M].北京:电子工业出版社,2006.(Wang Honghua.Mordern control theory[M].Beijng:Publishing House of Electronics Industry,2006)
RESEARCH ON STABLILITY OF GRAVITY TIME-VARYING SYSTEM
Guo Shusong1)and Zhu Yiqing1,2)
(1)Second Crust Monitoring and Application Center,CEA,Xi‘an 710054 2)Institute of Geodesy and Geophysics,CAS,Wuhan430077)
We regard gravity time sequence system as slow time-varying system and use difference equations for describing its equivalent parameter model based on the theory of linear systems analysis.By judging the stability of parametric sequence,we are going to explore the precursors.On the basis of gravity time-varying series from 1994 to 2009 of three observation points in Hexi gravity survey network,we prove that this method is effective,but more research are required to confirm the relations between unstability and seismic precursor anomalies.
gravity time-variation;slow time-varying system;difference equations;parametric sequence;Hexi gravity survey network
1671-5942(2011)05-0061-05
2011-03-09
国家自然科学基金(40874035);地震行业科研专项(20090829)
郭树松,男,1980年生,硕士,主要从事重力数据处理及应用研究.E-mail:98212541@sina.com
P315.72+6
A
