基于线特征计算像片外方位元素的理论与方法

孟庆堂，徐 琳

(1.信息工程大学测绘学院，河南郑州450052;2.61512部队，北京100088)

将式(9)代入到式(1)，经整理得到下式

基于线特征计算像片外方位元素的理论与方法

孟庆堂1，2，徐 琳1，2

(1.信息工程大学测绘学院，河南郑州450052;2.61512部队，北京100088)

依据空间直线在航摄像片上的投影仍然是直线这一前提，结合共线条件方程，通过线性化，推导基于线特征计算像片外方位元素的误差方程，并且给出计算过程。最后通过试验验证基于线特征计算像片外方位元素的理论与方法的可行性和可靠性。

线特征;外方位元素;空间后方交会

一、引 言

摄影测量学中的单像空间后方交会来源于测量学中的后方交会，而在测量学中的后方交会中，均采用精确的点。目前在摄影测量作业中，一般都要有若干精确的控制点作为计算依据，而在影像上和地面上找到精确的点都是一件难以实现的工作。相比之下，在影像上和地面上找到精确的线和面则更容易实现。虽然可以用影像分割的方法来提取面元素，但是面元素比线元素要复杂得多，用简单的兴趣算子往往不能很好地提取到理想的面元素，而线元素，特别是直线的提取要相对简单得多［1］。所以，本文从线特征着手，研究利用线特征计算像片外方位元素的理论和方法。

当前，有一些学者在研究利用线元素和面元素进行摄影测量参数的解算，如利用线特征进行相对定向和绝对定向［2］，对零件的尺寸进行检测［3］，对摄影测量的圆和圆角矩形进行三维重建［4］等。同时，张祖勋院士提出了广义点的概念［5］，而广义点不是真正的控制点，可以是线段，也可以是面。

在当前可以获取的数据中，往往能够很容易地获取精确的GIS三维坐标数据和遥感图像数据。同时，由于GIS数据具有属性特征，从而可以提取出一些特征线段;而在遥感图像中，利用兴趣算子也可以提取出一些线段。对这两种数据源进行匹配处理，就能实现线段的匹配，然后再把这两种匹配完成的数据作为初始数据，就可以自动进行像片外方位元素的解算。

二、线特征计算外方位元素的理论和方法

由飞机或卫星拍摄的数字影像，在摄影测量学作业中可以很容易地获取像片上对应地物的框标坐标，然后经过内方位元素改正得到相应地物的像坐标，而地物的GIS地面三维坐标也是可以从中获取的。

图1为以O为原点的像坐标系，假设坐标系中有一条直线，直线上有两个像点A、B;又假设地面上有一条直线，直线上两个点C、D，由于空间直线在航摄像片上的投影仍然是直线，可以假设两条直线对应，但点与点不一定对应。

图1 线特征计算外方位元素的示意图

在图1中，过点O作直线AB的垂线交直线AB于点O'，OO'即直线AB到原点O的距离ρ0，它和以x轴为正方向，逆时针旋转到OO'的角度θ0(0≤θ0＜2π)满足以下关系式［6］

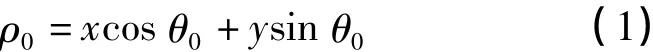
式中，(x，y)是线段的任意一个点。

ρ0和θ0分别满足如下关系

在图1中，地面点C(Xi，Yi，Zi)和D(Xi+1，Yi+1，Zi+1)组成的GIS直线与像坐标系下点A(xi，yi)和点B(xi+1，yi+1)组成的直线对应(但A不一定对应C或D，B也不一定对应C或D)。由于地面坐标与像坐标满足的关系是共线条件方程，所以(x，y)与地面坐标(X，Y，Z)存在如下关系［7］

式中，(X，Y，Z)是GIS数据中一直线上地面点的物方坐标;a1、a2、a3、b1、b2、b3、c1、c2、c3是物方空间坐标系与像空系之间的旋转参数;(XS，YS，ZS)是摄站在物方空间坐标系的坐标;f是相机主距。

设

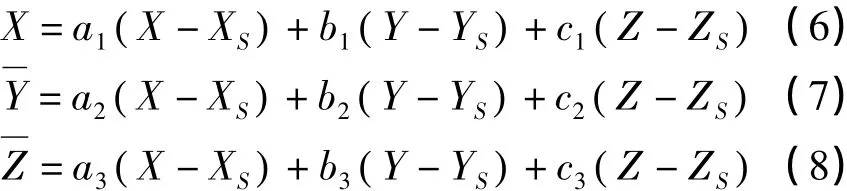
那么式(6)～式(8)可以用下式来表示

将式(9)代入到式(1)，经整理得到下式

假设外方位元素XS、YS、ZS、φ、ω、κ的初值为，则可以将外方位元素的初值计算代入式(11)得到

由于M计是由外方位元素的近似值计算得到，所以M计－M的大小与外方位元素初值的近似程度有关，设

假设外方位元素的改正数为dXS、dYS、dZS、dφ、dω、dκ，则可以用泰勒公式将M计－M表示为

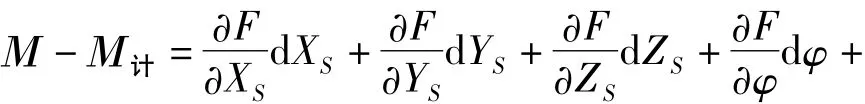
式(14)可以化为下式

式(15)就是用线特征计算像片外方位元素的一般形式，下面对各外方位元素进行偏微分。

设

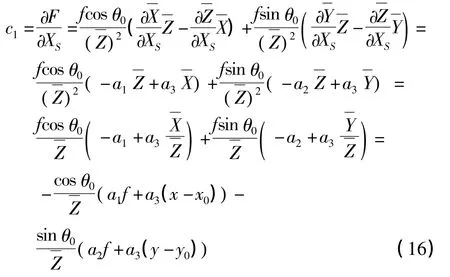
按相仿的步骤还可得出

而物方空间坐标系与像空系之间的旋转参数a1、a2、a3、b1、b2、b3、c1、c2、c3与外方位角元素φ、ω、κ之间存在一定的数学关系，参见文献［6］。

由式(16)～式(17)可以组建误差方程

式中，L=Μ－Μ计

三、线特征计算外方位元素的过程

1.读入原始数据

原始数据包括:影像的内方位元素，仿射变换参数，影像上直线段特征(至少3条，且两两不能在一条直线上)的扫描坐标和对应线段的GIS地面坐标。

2.确定外方位元素初值

(1)确定摄站坐标的初值

摄站的平面坐标(XS，YS)应由各GIS地面线段上点的平面坐标内插求得。若线段分布对称时，可取线段上点平面坐标的平均值作为摄影站平面位置的初值，摄影站的高度则可取相对航高。

(2)确定外方位角元素的初值

一般情况下，φ0=ω0=κ0=0。

3.组建误差方程式

组建误差方程式的步骤是:

1)按照式(2)和式(3)计算出各条线段的ρ0和θ0;

2)按照角元素的初值，根据式(16)、式(17)构建系数矩阵;

4)按式(18)组成误差方程

式中，A=［c1，c2，c3，c4，c5，c6］;ΔT=［dXS，dYS，dZS，dφ，dω，dκ］。

4.构建法方程

按最小二乘原理，构建法方程为

5.计算外方位元素的改正数

求解法方程，解外方位元素的改正数(dXS，dYS，dZS，dφ，dω，dκ)，得

6.修正像片外方位元素

按式(22)修正像片外方位元素

式中，k为迭代次数。

重复步骤3)～步骤6)的计算，直至外方位元素改正数的绝对值小于限差为止。

四、试验结果

为了验证本文采用的利用线特征计算外方位元素理论和方法的可行性和可靠性，与控制点计算出的像片外方位元素进行了比较。取一张拍摄广东某地区的航摄照片，拍摄高度1 800 m，像机主距156 mm，照片满足1∶10 000测图要求。在照片上找到4个分布比较均匀的点，计算出外方位元素，又在同样的像片上找到与GIS数据对应的13条线段(线段分布如图2所示)，计算出像片外方位元素。计算结果如表1所示。

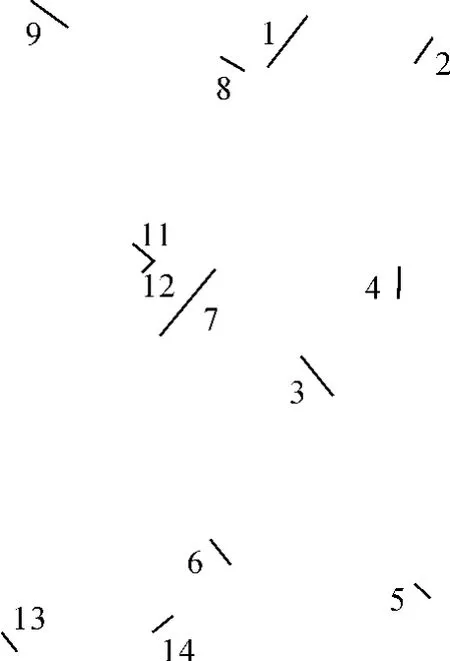
图2 线特征在照片上的分布图

表1 像片外方位元素的计算结果比对

从表1中可以看出，利用线特征计算外方位元素与利用控制点计算外方位元素得到的结果相似，表2是两种方法的结果比对。在计算出像片外方位元素后，重新将线段加载到航摄像片上，进行对比。图3是用控制点法计算结果叠加到影像上的效果。图4是线特征法计算结果叠加到影像上的效果(因为图幅太大，只显示第1条和第8条线的叠加效果)。

表2 两种方法计算出的结果比对

图3 控制点计算结果叠加在影像上的效果

图4 线特征计算结果叠加在影像上的效果

图3和图4表明两种方法计算出的外方位元素都能够满足精度需要，叠加到影像上的线段偏移量很小，用肉眼几乎无法察觉到两幅图像的区别。

五、结束语

利用线特征可以很好地计算出像片的外方位元素，而且精度可以满足需要。但在提取线段的同时，应该注意线段在像片上的分布情况应尽量分布均匀，而且线段的长度应该尽量长，以便减小计算结果误差。

［1］ 何乔，赵泳，张保明，等.基于广义点的相对定向和绝对定向［J］.海洋测绘，2006，26(4):7-9.

［2］ 张永军，张祖勋，张剑清.基于序列图像的工业零件尺寸检测技术［J］.上海交通大学学报，2003，37(9): 37-40.

［3］ 张永军.基于广义点摄影测量的圆和圆角矩形三维重建［J］.哈尔滨工业大学学报，2008，40(1):36-39.

［4］ 张祖勋，张剑清.广义点摄影测量及应用［J］.武汉大学学报:信息科学版，2005，30(1):1-5.

［5］ 殷硕文.一种基于线特征的高分辨率遥感影像配准方法［J］.测绘技术装备，2007，9(2):3-5.

［6］ 张保明.龚志辉.郭海涛.摄影测量学［M］.北京:测绘出版社，2008.

［7］ 何乔.张保明.郭海涛.基于广义点的定向方法［J］.测绘科学技术学报，2006，23(4):296-298.

The Theory and Method to Figure out Exterior Orientation Elements Based on Linear Feature

MENG Qingtang，XU Lin

0494-0911(2011)06-0005-03

P23

B

2011-04-15

孟庆堂(1974—)，男，安徽亳州人，硕士生，主要从事测绘工程管理工作。