对混合效应模型中参数估计的一个思考

金孝勇

（安徽师范大学数学计算机科学学院，安徽 芜湖 241003）

对混合效应模型中参数估计的一个思考

金孝勇

（安徽师范大学数学计算机科学学院，安徽 芜湖 241003）

将含有两个随机效应的混合模型，借助奇异值分解，等价转换成两个新模型，给出了一个固定效应的无偏估计，并指出在满足一定条件下其方差小于最小二乘估计的方差，同时证明了新模型中参数的最小二乘估计等于原模型参数的方差分析估计。

混合效应模型，奇异值分解，方差分析估计，最小二乘估计

对于含有两个随机效应的混合模型

其中，y 是 n×1 的观测量，Xn×t，Xn×s是已知的设计阵，βt×1是固定效应，ξs×1和εn×1是分别服从 N（0，）和 N（0，σ2I） 的随即效应.在模型(*)中， β、和 σ2估计是我们关心的问题之一.对此，有学者用岭估计方法来估计β，而对于和 σ2的估计问题，文献[1]、[4]中提及方差分析估计（ANOVAE）、极大似然估计（MLE）、限制极大似然估计（RMLE）、最小范数二次无偏估计（MINQUE）、谱分解估计（SDE）等方法，各有利弊，也有人基于均方误差、非负性等条件，对上述方法作出改进（见文献[2]、[3]），效果显著.

本文借助矩阵的奇异值分解，得到一个固定效应的新估计，并指出在满足一定的条件下，优于模型（*）中固定效应的LSE，同时证明模型（*）中参数σ2的ANOVAE等于一个新模型中参数σ2的LSE.文中用M（A）表示由矩阵A的列向量组成的空间，PA表示向M（A）的正交投影阵.

易知，模型（*）中可估函数 c′β的 LSE、σ2的 ANOVAE 分别为

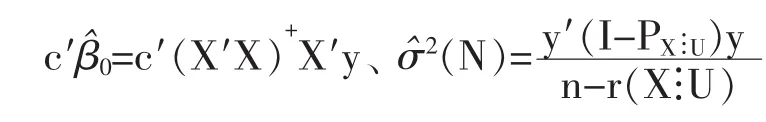
奇异值分解定理：设矩阵Am×n的秩为r，则存在两个正交阵P、Q，使得

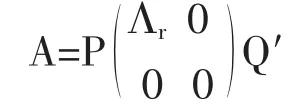
证明过程可参见文献[1].

下面对模型（1）中的设计阵U进行奇异值分解。设r（U）=r，可知存在正交阵P、Q，使

[1]王松桂等.线性模型引论[M].北京:科学出版社，2004.

[2]范永辉,王松桂.混合模型中方差分量估计的容许性及非负估计[J].应用概率统计,2008（4）.

[3]范永辉,王松桂.混合模型中方差分量的ANOVA估计的改进[J].高校应用数学学报,2007,22(1):67-73.

[4]王松桂，尹素菊.线性混合模型参数的一种新估计[J].中国科学（A版），2002，32.

A

1672－2868（2011）03－0025－03

2011-3-16

金孝勇（1986-），男，浙江宁波人。安徽师范大学在读研究生，研究方向：多元统计及其应用

责任编辑：陈 侃