平整机机架有限元分析
2011-11-11鞠德强姜富饶
鞠德强,赵 蔚,姜富饶
(鞍钢集团工程技术有限公司,辽宁 鞍山 114021)
1 前言
机架是轧机的重要零件之一,其尺寸和重量最大,在轧制过程中要承受较大的轧制力,同时要求机架变形要小,以满足产品的质量要求。为了保证轧机机架在工作中安全可靠,薄弱部位必须满足强度要求,为了保证轧制精度,其刚度必须满足刚度要求。近年来,采用弹性有限元分析方法研究机架最危险的位置及其应力的分布规律。本文采用材料力学的方法和有限元法进行互相验证,对鞍凌钢铁热轧1 700 mm工程平整分卷机组平整机机架的进行了优化设计。
2 鞍凌1 700 mm平整机参数
带钢机械性能 σs≤680 N/mm2

喂料速度 30 m/min
平整速度 300 m/min(max.)(带钢厚度1.2 ~4.5 mm) 270 m/min(max.)(带钢厚度4.5~6.35 mm)
平整压力 13 000 kN
平整力矩 80 kNm
液压AGC系统压力 28 MPa
平整机单侧弯辊力 ±500 kN
平整延伸率 ≤3%
单片牌坊重量 约57 t
牌坊断面积 约3 456 cm2
牌坊断面应力 约9.5 MPa
单个支承辊系的最大重量 约38.8 t
3 机架力学结构分析
3.1 建立三维模型
应用有限元法对机械零件进行力学分析的基础是建立一个零件实体基本相当的1:1的三维模型,由于实际零件比较复杂,在建立模型过程中必须进行合理地简化。在本平整机设计过程中,采用Soildwork建模,其模型如图1所示。模型材料为ZG270-500,弹性模量E=2.06 MPa,泊松比ν=0.3。图2为机架结构尺寸图。

图1 机架模型
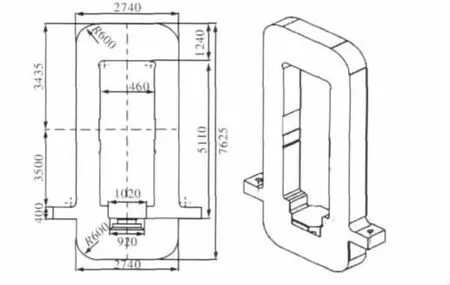
图2 机架结构尺寸图
3.2 模态分析
模态分析可以很直观地了解到机架在不同频率下的变形情况。根据现场情况和模态分析结果,对机架进行优化设计,避免产生共振损坏设备。本机架完整模型的前16阶频率及振型如表1。

表1 机架完整模型的固有频率及振型
利用单机架的计算模型,求得前6阶模态振型,结果如表2和图3所示。

图3 单机架前6阶模态振型
从表1、表2可以看出,该机架有四种主要的振动类型,其中机架 Z向弯曲振动(1、8、14、15阶振型),从结构尺寸可以看出机架沿Z向弯曲时其抗弯刚度系数最小,说明一阶振动是结构最容易发生的振动形式,符合材料力学理论。
两种模型的第一阶模态振型都是沿Z轴方向摆动,但是频率相差很大。单机架的固有频率为8.378 Hz,而完整模型的第一阶固有频率为12.575 Hz。这是由于完整模型的两片机架由上连接梁刚性连接使其刚度加大,而单机架不能准确地反映实际的装配关系,计算结果与实际产生了较大的偏差,因而完成模型的模态更接近实际情况。
3.3 用能量法求解机架第二阶固有频率[1]
能量法是计算自振频率比较有效的方法之一。根据能量守恒定律,当体系以某个频率自由振动时,在不考虑阻尼的情况下,体系无能量损失,因而在任意时刻,体系动能与变形能之和为一常数,当体系在振动中达到幅值的时刻,动能为零,而变形能达到最大值。反之,当体系在静平衡位置的瞬间时,动能有最大值,变形能为零。利用这一关系式即可得到确定频率的方程。

由于在对机架进行结构动力计算时,将其简化成刚架结构,外形尺寸简化成机架结构的中心尺寸,约束由原四点螺栓刚性连接简化成两点固接。从计算所得第二阶固有频率20.269 Hz,Ansys软件分析第二阶固有频率19.958 Hz,均在误差范围内。
3.4 强度与刚度分析
在轧制过程中,机架受力很复杂,包括轧制力、摩擦力、附加力、冲击力等,但以轧制力为最大,其它远小于轧制力,可以忽略,因此本文只取轧制力为外载荷。
3.4.1 载荷施加
在正常轧制时,机架所受的轧制力为13 000 kN,每片牌坊承受一半,即6 500 kN,作用面积0.54 mm×1.46 mm=0.7884 mm2,所以均布载荷为8.2 MPa,作用在上横梁截面上及下横梁AGC缸承载面上。
3.4.2 约束条件
根据现场机架的安装情况,机架地脚螺栓连接处为刚性约束。
3.4.3 有限元计算结果与分析
用有限元法可求得机架各个部位的等效应力及其相对大小分布如图4所示。由图4可见机架的内侧应力大于外侧,而中间部位的应力值最小,机架立柱的内侧应力值为10.458~12.197 MPa之间,外侧应力值为8.719~10.458 MPa之间,上横梁外侧应力值为12.197~15.674 MPa之间,其中最大处为应力集中是最大位置。

图4 机架应力云图
由图5可知,机架在水平方向的最大变形出现在左右立柱上,变形表现为立柱向轧机窗口内侧弯曲,其中左右立柱最大变形量约为0.170 29 mm,机架水平方向总变形量为0.344 18 mm;机架在垂直方向的最大变形出现在机架上下梁,上横梁变形最大,变形量为0.349 55 mm,下横梁的最大变形量为0.150 07 mm,机架垂直方向总变形量为0.499 62 mm[2]。
如图6所示,单机架在水平方向上的最大变形量为0.29109 mm(0.14516+0.14593),单机架在水平方向上的最大变形量为0.42797 mm(0.28889+0.13908)。单机架模型与完整模型结果的偏差是由于计算中忽略了连接梁,完整模型的计算结果更接近真实值。

3.4.4 材料力学的计算
机架强度计算采用材料力学的方法计算,选取较大的安全系数,以保证机架的强度。本文采用参考文献[1]的算法进行计算,以验证ANSYS分析的正确性。
经过计算得
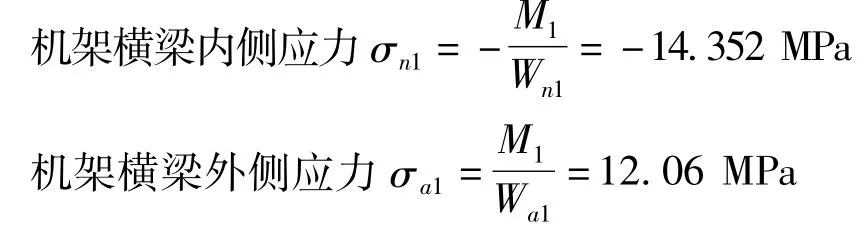
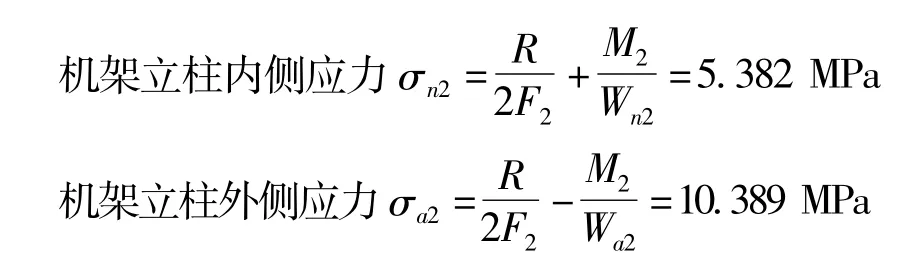
机架的变形计算
机架的弹性变形是由横梁的弯曲变形和立柱的拉伸变形组成的,由于横梁的断面尺寸较横梁的长度来说是较大的,在计算横梁的弯曲变形时,应考虑横向切力的影响,即

式中,f3为机架的弹性变形;f′3为由弯矩产生的横梁的弯曲变形;f″3为由切力产生的横梁的弯曲变形;f‴3为由拉力产生的立柱拉伸变形。
根据卡氏定理,由弯矩产生的两横梁的弯曲变形为
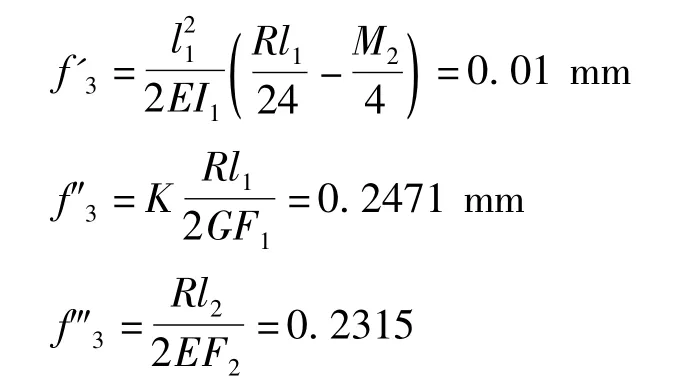
则机架的弹性变形为
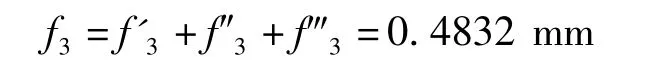
由此可见应力通过材料力学的方法计算出来应力值、变形量与ANSYS软件分析的结果基本一致的。
4 结束语
本文利用ANSYS建立了平整机机架的有限元模型,对机架在工作载荷下的模态、应力和变形进行了三维分析,获得了平整过程中的机架振动频率、变形、位移及应力场分布等详细的定量数据,由此不仅揭示了机架机构的薄弱环节,还为平整机的刚度与强度设计及工程分析提供了更为可靠的科学依据,同时通过了材料力学与结构力学的计算,对比了所得出的结果,使分析与计算更加的真实可靠,为其他的设备的设计提供了方法。
[1] 黄华清.轧钢机械[M].北京:冶金工业出版社,1979.
[2] 邹家祥.冶金机械的力学行为[M].北京:北京科技出版社,1999:25-32.
