闭式机架横梁静不定力矩的柔性转角计算法

莫军晓

(中冶陕压重工设备有限公司，陕西 西安 710109)

1 前言

用材料力学方法计算闭式机架横梁的静不定力矩时，由于对机架建立的矩形自由框架模型假设机架横梁与立柱转角处是刚性的［1-5］，忽略了机架转角处的变形，计算结果偏离实际情况。

本文提出一种柔性转角计算法。考虑机架横梁与立柱转角处存在的角变形，并利用该角变形与所受弯矩的关系，求出横梁静不定力矩和角变形的关系，进而通过卡氏定理求解，得出横梁静不定力矩的函数表达式。

本方法经过实例检验，计算数值结果有足够高的精度，并且避免了冗长的数值运算，可以作为建立更复杂控制模型的基础工具。

2 柔性转角计算法

计算上横梁中部的静不定力矩时，因方法的差别而导致不同的结果，但是当静不定力矩数值求解出来后，其他诸如各个特征点的应力、应变和位移的计算过程，各种计算方法则大致相同。

本方法认为机架转角处存在附加的、相对的转角变形，并且是可以计算出来的。

转角变形量的大小和立柱上的力矩直接相关，呈线性正比例关系。转角变形量由四个部分组成，分别是力矩对上横梁、立柱上部、立柱下部、下横梁产生的变形。对应的变形值分别用θ1、θ2、θ3和 θ4表示，如图1 所示。

图1 横梁与立柱转角处变形分解示意图

将机架横梁看作纯弯曲梁，受弯后的转角和受弯时的中性层曲率半径分别用下式计算。

式中，l为弯曲梁长度;θ为弯曲梁受弯后的转角，即角变形量;ρ为弯曲梁中性层曲率半径;E为材料弹性横量;I为惯性力矩;M为弯曲梁的弯矩。

上、下横梁和立柱上、下部都可以看作特殊形式的纯弯曲梁，呈倒三角形布置，其弯曲变形是由纵向平行侧面构成的长方体纯弯曲梁的二分之一，因而转角变形量也相应减半。

式中，θ1～θ4分别为上横梁、立柱上部、立柱下部和下横梁的角变形量;I1～I3分别为上横梁、立柱和下横梁的惯性力矩;M1、M2分别为上横梁和立柱的弯矩;R为轧制力;L1为上、下横梁中性线长度;b为立柱宽度;h为横梁高度。

如图2所示，机架上横梁中部的转角等于零，利用卡氏原理，求解上横梁的静不定力矩M1，然后得出立柱力矩M2。

式中，Ix为任意截面的惯性力矩;y为轧制力相对于任意截面的力臂;x为任意截面上机架中性线长度。

图2 矩形自由框架弯曲力矩图

通常取I1=I3，另外运用近似计算arcsinx≈x，式(5)进一步表达为

由式(9)知，柔性转角法与材料力学法的区别也在于柔性转角法考虑了机架的形状参数Δ。

机架计算模型基本尺寸如图3所示，式(9)可表示为:

图3 机架计算模型基本尺寸图

式中，t为机架厚度。

3 计算实例

图4为某轧钢厂750 mm四辊冷轧机机架［6］本文分别用材料力学法、小圆弧法、精确圆弧法、有限元法以和柔性转角法对该机架进行强度计算。计算结果见表1。

图4 机架尺寸图

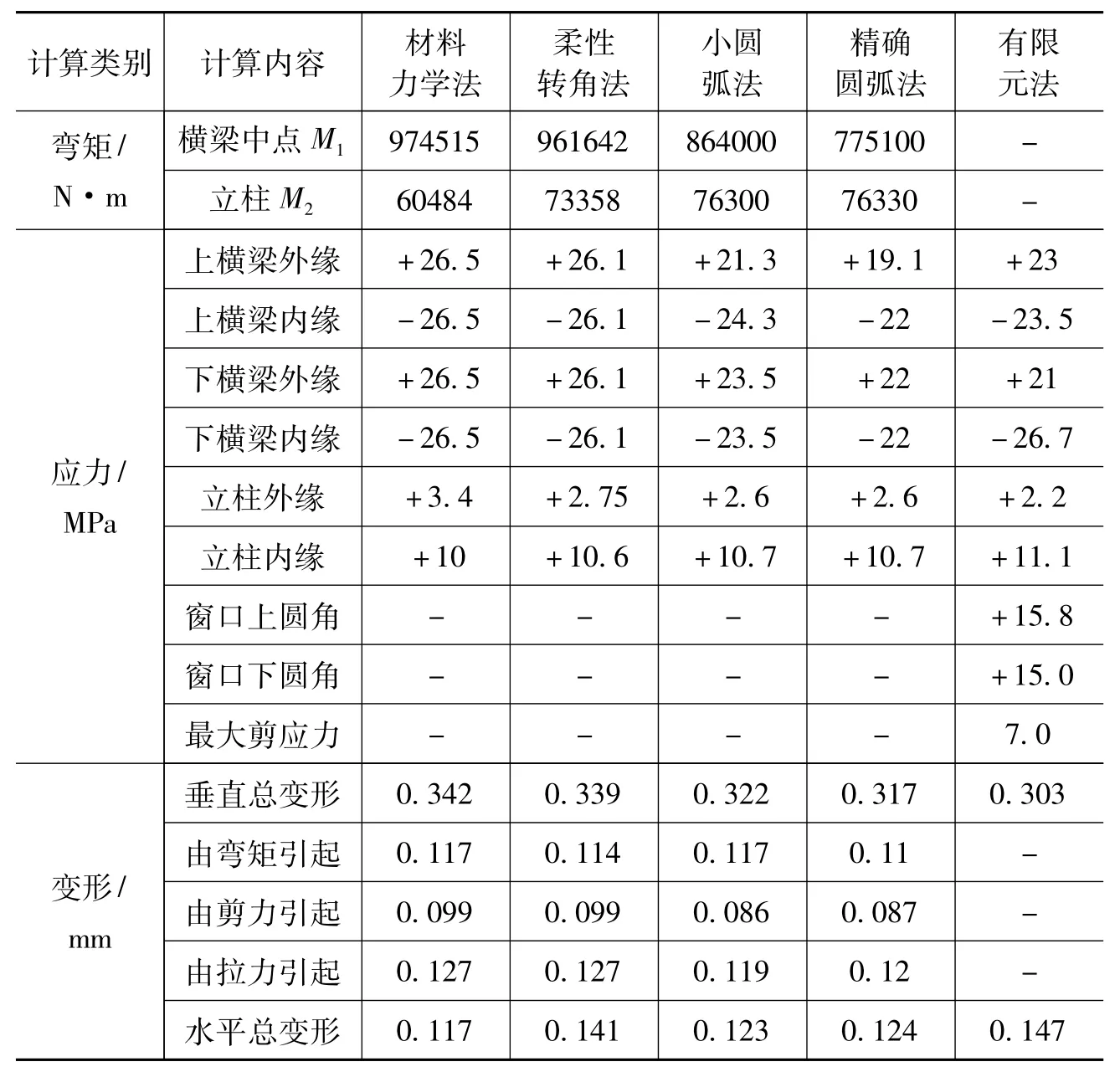
表1 计算结果

表1中用材料力学法和柔性转角法计算的M1与M2的总和相同。柔性转角法计算出的M1比材料力学法小，因而M2能大些。但是M2更接近小圆弧法和精确圆弧法的计算结果。小圆弧法和精确圆弧法计算的M1与M2要小，导致计算出的横梁外缘应力数据偏小。

由于材料力学法和柔性转角法忽略了上下横梁的形状差异，应力计算结果表明上下横梁内外缘应力数据为对称分布，与实际情况有较大差别。小圆弧法和精确圆弧法可以如实地反映机架真实的形状及变化过程，上横梁内外缘应力数据应该和上横梁内外缘应力数据有所不同，所以计算结果大部分与有限元法比较接近。

精确圆弧法计算的垂直方向变形最接近有限元法计算结果，而水平方向变形的计算则以柔性转角法最为准确。

4 结论

柔性转角法与材料力学法、小圆弧法和精确圆弧法都是闭式轧机机架的解析算法。材料力学法算法简单，计算结果偏于保守;小圆弧法和精确圆弧法计算过程冗长、模型分段复杂，计算结果相对准确;柔性转角法算法比较简单，计算结果也比较准确，有一定的参考价值。

［1］ 刘鸿文．材料力学［M］．北京:高等教育出版社，2004．

［2］ 邹家祥．轧钢机械［M］．北京:冶金工业出版社，2005．

［3］ 乔治．板带车间机械设备设计［M］．北京:冶金工业出版社，1984．

［4］ 施东成．轧钢机械设计方法［M］．北京:冶金工业出版社，1990．

［5］ 欧光辉．轧机版坊强度与钢度的精确计算［J］．重型机械，1980，(1)．

［6］ 莫军晓．750 mm四辊带钢冷轧机机架有限元分析［J］．西重科技，1991，(2)．