疏松砂岩临界生产压差参数求解方法研究

康 凯,冯 敏,李彦来,李其正,苏彦春,刘 超

(中海石油(中国)有限公司天津分公司,天津塘沽 300452）

疏松砂岩临界生产压差参数求解方法研究

康 凯,冯 敏,李彦来,李其正,苏彦春,刘 超

(中海石油(中国)有限公司天津分公司,天津塘沽 300452）

依据Mohr-Coulomb准则,利用弹性和弹塑性理论,建立防止疏松砂岩油藏出砂的临界井底流压模型,可较准确求解地层出砂临界生产压差。针对模型涉及弹性力学参数测试费用昂贵、难以获取等难题,提出一套不需测试的参数确定方法。旅大5-2油田应用本方法,得到的临界生产压差与油井实际基本一致,结果符合率高、误差小,该方法具有明显的经济意义和实用价值,可广泛的应用于类似疏松砂岩油藏。

疏松砂岩;临界生产压差;地层内聚力;动态泊松比;地层内摩擦角

疏松砂岩油藏出砂一般分为两种,充填砂出砂和骨架出砂。实践证明,充填砂适度出砂可疏通地层孔隙通道、提高原油流动能力,产生有利影响,生产过程中要避免的是岩石骨架出砂。

出砂与否与储层骨架颗粒和胶结物之间的交接方式、胶结强度、地层应力状态和油气生产的作业方式、环境、条件有关。油气储层岩石在地应力及流体流动力的作用下,产生剪切破坏或拉伸破坏时就可能会造成出砂。

1 油层出砂力学模型建立

Mohr-Coulomb准则认为:当岩石破裂面上的剪切应力τ等于岩石材料本身的抗剪强度(即内聚力C)与作用于该破裂面上的正应力σ引起的内摩擦阻力σtgθ(θ为地层内摩擦角)之和时,发生剪切破坏,造成岩石骨架出砂。Mohr-Coulomb准则关系式[1]为:

油井不出砂最小井底压力[2],即临界井底流压Pwcr为:

式中:C——地层内聚力 ,MPa;σzo——上覆岩层压力,MPa;μd——动态泊松比,取值一般小于 0.25;β——孔隙弹性介质Biot常数,小数;Pe——油藏外边界处压力 ,MPa;θ——地层内摩擦角,°。

油层出砂临界生产压差ΔPcr为:

2 参数求解方法

临界生产压差的求解过程中,砂泥岩内聚力、动态泊松比、上覆岩层压力、地层内摩擦角、孔隙弹性介质Biot常数等参数求解难度较大;纵波速度、岩石体积密度、泥质含量及油藏外边界压力相对较易取得。

2.1 砂泥岩内聚力 C的确定

砂泥岩内聚力 C与声波传播速度Vp的关系[3]:

式中:ρb——岩石体积密度 ,g/cm3;νp——纵波速度,m/s;Vcl——泥质含量,%;

2.2 动态泊松比μd的确定

采用实际岩心进行实验,可以获得动态泊松比μd数值,一般油田缺乏实测资料,疏松砂岩通常情况可取0.13。

根据岩石弹性力学理论,岩石泊松比是纵横波时差的函数[3]。

式中 ,Δts——岩石的横波时差 ,μs/ft;Δtp——岩石的纵波时差,μs/ft。

并不是所有的测井系列都开展声波全波列测井或偶极横波测井。为此,部分学者开展利用纵波时差等常规测井资料求取岩石泊松比的研究,建立利用地层泥质指数、岩石纵波时差、中子测井孔隙度和自然伽马值求取岩石泊松比的统计模型[4]。

式中,ΦN——中子孔隙度,%;GR——自然伽马值,API;Ish——地层泥质指数;Φs、Φd——声波时差和地层密度测井求得的孔隙度,%。

随着动态泊松比的增大,临界生产压差降低。

2.3 上覆岩层压力σzo的确定

上覆岩层压力也称为围岩压力,是整个上覆岩石地层所施加的压力。密度测井曲线可以比较真实地反映地下岩石的体密度随其埋藏深度的变化规律,是求取上覆岩压力最为理想资料,通过密度曲线积分求取σzo[5]。

式中,ρb(H)——H深度处的岩石体积密度,g/cm3;g——重力加速度,9.8m/s2;h——所计算的油层深度,m。

并不是所有井的密度测井都是全井段的,依靠积分求解有时存在一定难度,一般情况下,可采用上覆岩层压力梯度的理论值22.7kPa/m计算。

假设上覆岩层压力随深度均匀增加,则:

式中,ρ岩——岩石骨架平均密度,g/cm3,通常取值2.5g/cm3;ρ流——流体平均密度 ,g/cm3,通常取值1.0g/cm3;Φ平——平均孔隙度 ,%,通常取值10.0%。

随着上覆岩层压力增大,临界生产压差减少。

2.4 地层内摩擦角θ的确定

一般岩石的内摩擦角θ与内聚力C之间有关系[3]:

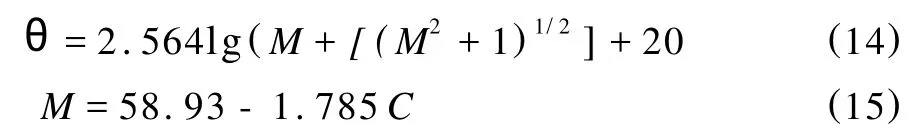
2.5 孔隙弹性介质Biot常数

对于疏松砂岩来说,孔隙弹性介质Biot常数通常取值1.0。

研究表明,根据经验方程[6]可以确定静态Biot弹性常数:

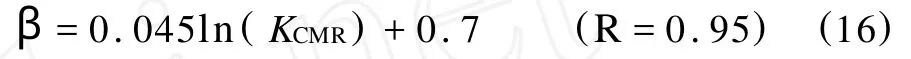
式中,KCMR——用核磁共振测井(CMR)解释的渗透率 ,10-3μm2。

随着孔隙弹性介质Biot常数的增大,临界生产压差减少。

2.6 纵波速度νp的确定

应用测井资料可以获得为纵波速度νp,计算公式为:

随着纵波速度的增大,临界生产压差增大。

2.7 岩石体积密度ρb的确定

岩石体积密度ρb并非岩石骨架密度,该值可从常规密度测井直接得到。

随着砂岩密度的增大,临界生产压差增大。

2.8 泥质含量Vcl的确定

泥质含量Vcl指的是岩石中具有胶结作用的粘土含量。应用测井资料得到泥质含量数据,包含了粘土含量以及部分细粉砂、束缚水等,测井解释结果偏大,不具备使用意义。准确的泥质含量Vcl数据应来源于岩心化验分析资料。随着泥质含量的增大,临界生产压差增大。

3 油田应用效果

LD5-2油田位于渤海海域,主要目的层为东营组东二上段,湖相三角洲前缘沉积,油藏埋深浅,储层胶结疏松,泥质含量较低,为2%左右。

采取上述方法,进行LD5-2油田出砂临界生产压差计算,见表1。

利用油井出砂时的生产压差,验证临界生产压差计算结果的准确性,见表2。

临界生产压差与油井开始出砂时实际生产压差基本一致,二者平均相差0.13MPa,误差为5.1%,计算结果精度较高好。对比结果说明:

(1)依据Mohr-Coulomb准则,利用弹性和弹塑性理论,建立的防止疏松砂岩油藏出砂临界井底流压模型,可较准确地求解地层出砂临界生产压差,差,计算结果真实、可靠,准确率高;

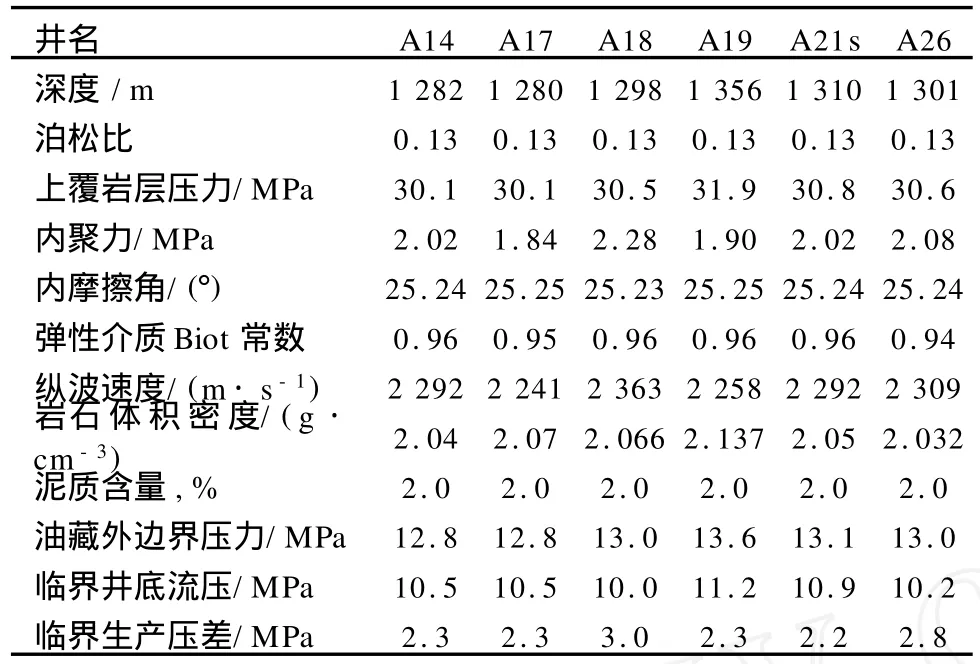
表1 LD5-2油田部分油井临界生产压差计算结果

表2 油井出砂阶段生产压差与临界生产压差对比

(2)参数确定方法实用性较强,计算结果可以满足油田日常生产需要,使用该方法可节约大量的弹性力学参数测试费用、测井费用,具有明显的经济意义和实用价值。

4 结论与建议

(1)依据Mohr-Coulomb准则,利用弹性和弹塑性理论建立的临界井底流压模型,可较准确地求解地层出砂临界生产压差。

(2)本文提出的临界井底流压模型参数确定方法实用性较强,计算结果与油井实际吻合度较高,可基本满足油田日常生产管理需要。

(3)为避免LD5-2油田东二上段油井出砂,建议合理生产压差小于2.20MPa。

[1] 王勤田,越彦超,杨晶,等.油井出砂临界井底流压计算模型及应用[J].江汉石油学院学报,2002,24(2):75-76.

[2] 陈民锋,姜汉桥.渤中25-1南油田不同井型油井合理生产压差研究[J].中国海上油气,2006,18(6):399-402.

[3] 李天太,张益,张宁生,等.地层力学特性参数求解及其在苏里格地区的应用[J].西安石油大学学报(自然科学版),2005,20(5):22-24.

[4] 刘之的,夏宏泉,陈平.岩石泊松比的测井计算方法研究[J].测井技术,2004,28(6):508-510.

[5] 褚义.萨北开发区破裂压力梯度研究[J].大庆石油地质与开发,2006,25(增刊):23-24.

[6] 曹文杰.NMR在与岩石力学相关的出砂控制、水力裂缝和井眼稳定性等石油方面的应用[J].测井技术信息,2003,16(6):42-45.

TE313

A

1673-8217(2011)02-0058-03

2010-08-10

康凯,1978年生,2003年毕业于江汉石油学院,获硕士学位,现从事油气田开发方面研究。

编辑:彭刚