高超声速前缘空腔数值模拟研究
2011-11-08耿云飞
耿云飞,阎 超
(北京航空航天大学国家计算流体力学实验室,北京 100191)
0 引言
对于高超声速远程机动飞行器,前缘形状是影响气动力、气动热的关键因素之一。为了获取高升力、低阻力等优良气动力性能,应当采用尖锐前缘(如高超声速“乘波体”);而出于防热的需求以及制造加工等考虑,尖锐前缘又必须进行足够的钝化。这一矛盾要求使得高超声速飞行器前缘设计必须进行折中。近年来,不少国外文献研究了在前缘点引入空腔的被动控制概念,并进行了大量的试验与数值模拟研究,指出空腔唇口外缘局部将形成“冷却环”,可有效降低当地的热流。
前缘空腔是1922年 Hartmann和 Troll[1]在研究产生不连续频率的高强度声音时发现的(当时被称作“Hartmann哨”技术),这项技术就包括超声速喷流流过一个带前缘空腔的外形,之后关于前缘空腔的研究就不断开展起来了。1959年 Burbank和 Stallings[2]研究发现,具有前缘凹腔的轴对称体的驻点热流率要比常规的凸前缘小很多。Johnson[3]研究高超声速前缘空腔氦气绕流是发现空腔内流场的强烈不稳定现象。Baysal和Stallings[4]采用上风松弛格式的二维N-S方程计算了半模的面对称前缘空腔飞机。Marquart和Grubb[5]在Arnold工程发展中心完成了对具有前缘空腔的钝头模型脱体弓形激波动力学、声学共振以及激波抖动等方面的高超声速风洞测试。Huebner和Utreja[6]的研究发现前缘弓形激波的振荡频率以及振幅与空腔深度有直接关系。Yuceil和Dolling[7]用红外摄像机研究表明,较大直径的浅空腔在空腔唇口附近产生一个稳定的冷却环,使得局部温度比普通球锥的值要小。
风洞实验的来流不可避免地具有一定的扰动,因而前缘空腔内出现强烈的压力共鸣是实验中一个普遍的流动特征;数值计算时,如果人为给来流施加一定的扰动或者应用足够深的空腔时也会出现这种抖动现象。此时,强烈的空腔径向压力抖动会引起前缘激波的抖动,从而可以使空腔唇口的壁面降温。但是,空腔前缘的周期性激波抖动可能会对飞行器的结构以及飞行特性带来不利影响,并且当空腔内流动处于流入空腔的半周期时,壁面热流是处于增大的趋势的。本文尝试将前缘空腔技术应用于高超声速飞行器的前缘设计,在研究时将L/D(空腔的深度与空腔直径之比)限制在0.1~2以内,在H=50km高度的大气参数下,流动均处于定常状态,不会出现空腔内压力抖动。此时通过合理的空腔参数设计,仍可达到降低前缘壁面热流率的目的。
1 数值方法及验证
1.1 控制方程
控制方程采用薄层假设的三维可压非定常的NS方程(TLNS方程),在一般坐标系下可写为如下形式:
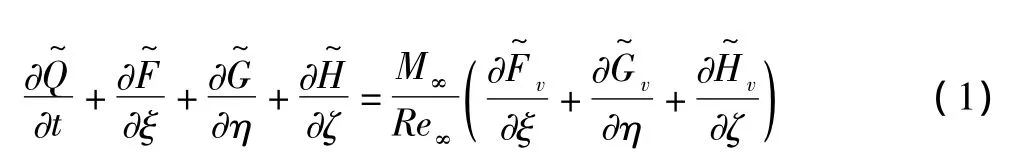
温度可以通过理想气体状态方程由密度和压强求得:
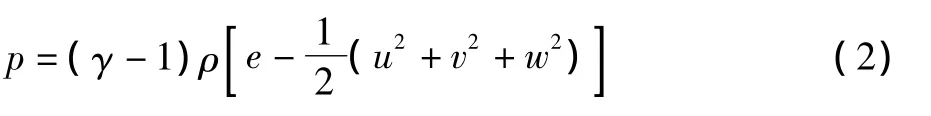
壁面热流由下式计算:
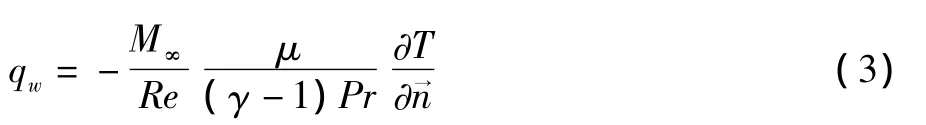
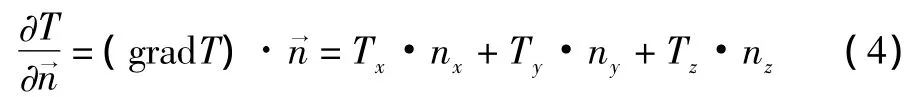
其中
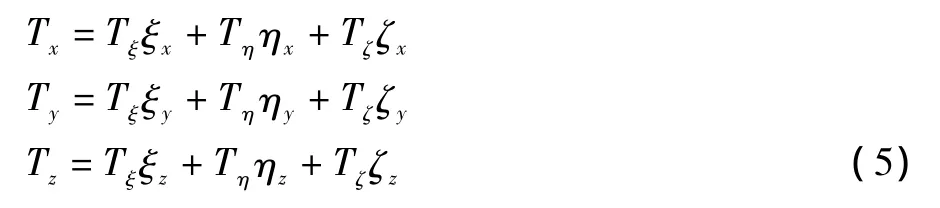
1.2 数值方法
采用有限体积方法对NS方程进行离散,对流项采用Roe's FDS格式进行离散,并采用MUSCL插值使其达到二阶精度,限制器采用minmod限制器;粘性扩散项采用二阶中心差分。为提高计算效率,采用时间一阶精度的隐式离散格式,求解时应用LU分解技术。
边界条件取远场边界为无反射边界条件,物面边界为粘性流动的无滑移条件;固壁为等温壁,壁面压力按法向零压力梯度取内场点一阶插值;全场取自由来流值为初始条件。
1.3 算例验证
为了对本文计算程序进行验证,本文选取了钝双锥外形进行了数值模拟并同实验值进行了对比。计算的来流条件为[8]:Re∞=2.318 × 105,T∞=48.88K,Tw=300K,ρ∞=4.271 ×10-3kg/m3,迎角 α =10°,模型长度为122.24mm,头部曲率半径3.835mm。钝双锥的几何尺寸如图1所示。
对于热流计算,网格收敛性是必须要考虑的。本文对不同网格雷诺数[9]下的钝双锥驻点热流进行了研究(如图2所示,其中网格雷诺数 Rec=ρ∞V∞n/μ∞,n为法向第一层网格高度),结果发现在网格雷诺数小于20以后,驻点热流值已基本收敛,继续加密网格对热流的计算结果不再产生影响。为了保证热流计算的网格无关性,本算例在计算时取网格雷诺数为5。图3给出了外形的空间网格。
图4给出了钝双锥的对称面等马赫线图,可见程序对于激波以及背风面的滑移线均可正确地捕捉到。图5给出了钝双锥壁面热流沿轴向的分布,图中横坐标表示归一化的轴向距离,纵坐标均为归一化热流,即当地热流与驻点热流的比值。可见CFD结果与实验结果吻合的很好,双锥对接处由于膨胀引起的冷却效应等热现象也可精确地捕捉到,验证了本文计算网格的网格收敛性以及计算程序的可靠性。
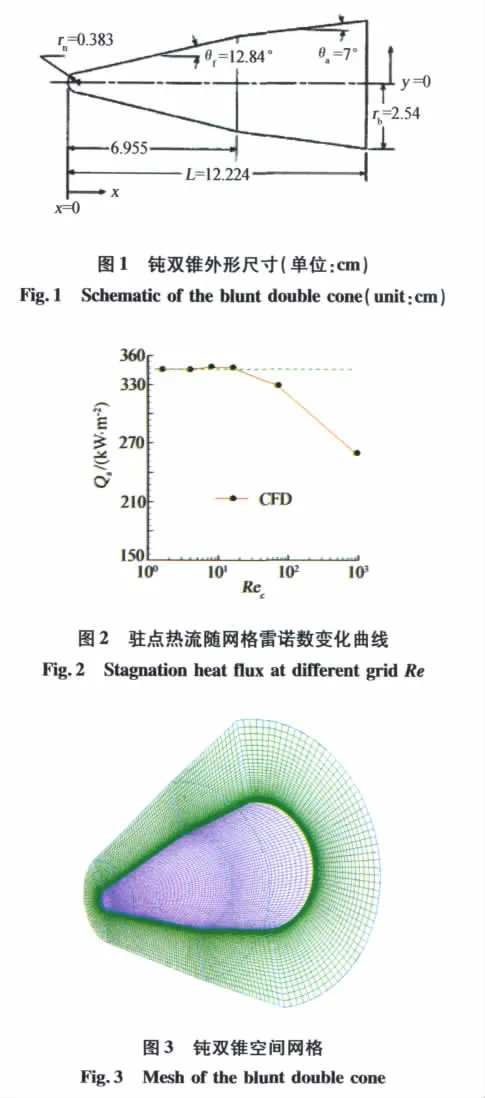
为了保证热流计算的网格无关性,下文中计算网格均保证网格雷诺数在10以下。

2 计算结果及分析
本文选取高超声速飞行器经常采用的前体外形——轴对称钝锥外形,作为研究的基准外形(图表中以“base”表示),钝锥的总长度为1m,半锥角为5°,头部钝化直径D为10mm。在此基准外形的基础上,进行前缘空腔处理,根据不同的前缘线型、前缘钝化半径、空腔生度等参数衍生出不同的前缘空腔外形。图6给出了基准外形以及前缘空腔外形的头部放大图。
计算的来流马赫数取为6.0,来流大气的参数与50km高度处空气的值相同;等温壁条件为Tw=600K。
2.1 前缘线型及钝化半径的影响
首先研究了空腔不同前缘线型对最大热流以及气动力的影响,分别选择了sharp、medium、blunt三种不同的前缘线型(如图7所示)进行对比,空腔L/D均为1.0。

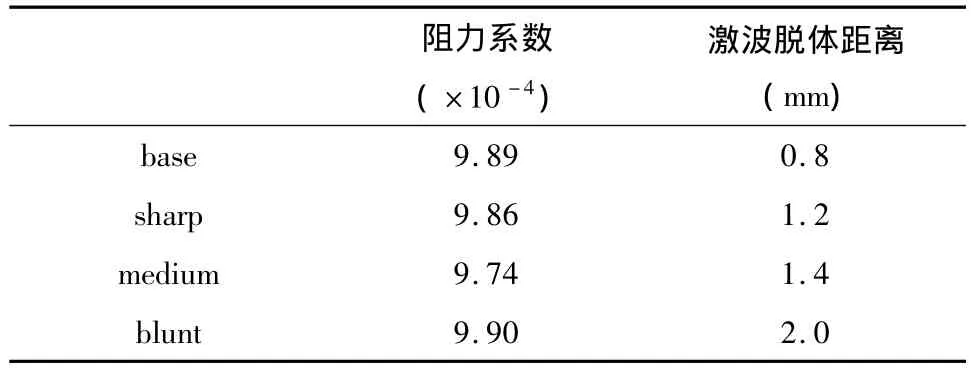
表1 基准外形以及不同前缘线型空腔外形气动力系数计算结果Table 1 Comparison of the aerodynamic coefficient
表1给出了不同前缘线型的空腔外形总阻力系数计算结果(为方便计算,参考长度和参考面积均取为1)以及前缘的激波脱体距离,其中的激波脱体距离为弓形激波距空腔前缘点在轴线上投影位置的距离。可以看出,不同线型的总阻力值基本与基准外形的阻力值相等,但头部激波的脱体距离却远大于基准外形对应的值,并且随着前缘线型趋于钝化,激波的脱体距离逐步增大。
图8给出了不同前缘线型的空腔外形头部壁面最大热流同基准外形的比较。当前缘线型为半圆弧时,空腔外形前缘的最大热流值已经低于基准外形的驻点热流值。
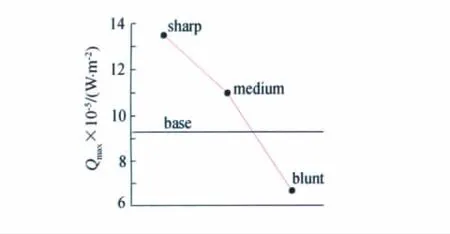
图8 不同前缘线型的前缘最大热流值对比Fig.8 Comparison of the maximum wall heat flux
图9给出了blunt前缘线型的轴对称前缘空腔外形对称面流场图及局部流线图,在空腔前缘形成一道正激波,流动经头部弓形激波后,受空腔的阻塞作用在空腔内形成一个高压回流区,在该回流区影响下头部激波脱体距离将增大,从而有利于壁面热流的降低。

图9 对称面流场图Fig.9 Flow fields on symmetry plane
之后又对blunt线型进行了增大钝化半径的对比研究,前缘钝化半径由原来的1.6mm增大至2.0mm,结果发现前缘钝化半径增大后,前缘的最大热流值明显减小(相对基准外形值降低了16%),而对阻力基本没有影响。
2.2 不同L/D的影响
前缘线型采用上节blunt线型,对L/D分别为0.1、0.5、1.0和2.0时进行了对比研究。结果发现在本项目研究条件下,不同L/D的空腔外形相应的气动力和空腔前缘热流分布也基本不受L/D的影响。图10给出了不同L/D参数的前缘空腔外形壁面热流对比,可以看出不同L/D的空腔外形的前缘热流分布基本重合。这是由于空腔的继续加深不会对流场产生本质的影响,空腔内的压力基本保持等于波后气体的总压,激波脱体距离保持恒定,空腔的后段基本是死水区。
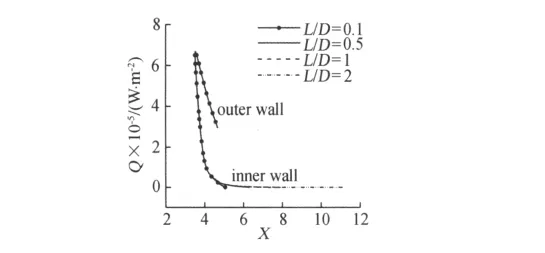
图10 不同L/D外形壁面热流对比Fig.10 Wall heat flux comparison of different L/D configurations
2.3 不同攻角和马赫数下的结果
以上结果均是在马赫数6.0、0攻角状态下得到的结果,为了进一步考察前缘空腔外形在不同攻角、不同马赫数下的特性,本文进行了进一步研究。对50km高度下,空腔外形(钝前缘线型,Rn=1.68mm,L/D=1.0)在Ma=6.0时进行了有攻角状态的数值模拟。考虑到高超声速飞行时攻角不会太大,因此攻角范围限制在0°~12°。最后对该外形在马赫数4~7范围内进行了对比研究。
图11给出了Ma=6.0时不同攻角下空腔外形和基准外形升阻比的对比,可见空腔外形和基准外形不同攻角下的升阻比基本重合,空腔并没有影响外形的升阻比特性。而对于热流,从图12给出的不同攻角下空腔外形和基准外形壁面最大热流值的对比可以看出,空腔外形的壁面最大热流值在有攻角状态虽然相对0攻角时略有上升,但始终低于基准外形的热流值(相对基准外形最大热流值降低20% ~30%)。需要指出的是,有攻角状态的最大热流值出现在空腔的迎风面前缘,因为有攻角状态时前缘正激波不再对称,而是迎风面的激波更加靠近壁面,背风面的激波远离壁面,因此迎风面的热流峰值在有攻角时要略高于无攻角状态的值,且随攻角的增大而增大;而背风面的热流峰值在有攻角时要远小于无攻角状态。

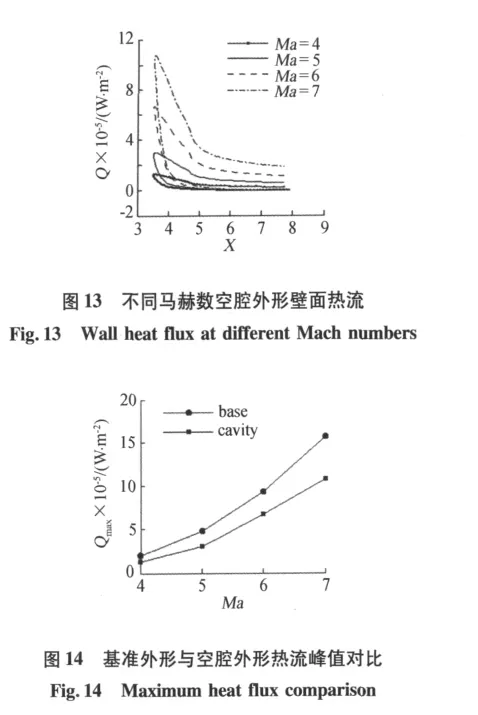
图13给出了0°攻角时不同马赫数的空腔外形前缘壁面热流值分布,随着马赫数的增大,空腔外形的前缘热流极值以及外壁面的热流值均明显增大。图14给出了不同马赫数下基准外形和空腔外形前缘最大热流值的对比图,可以看到,不同马赫数下空腔外形均能有效降低前缘的热流值。
3 结论
针对高超声速飞行器所面临严峻的气动加热问题,对采用前缘空腔的轴对称高超声速钝锥外形进行了数值模拟研究,在本文研究范围内得到以下结论:
(1)高超声速条件下,合理设计的前缘空腔外形能够避免空腔内的压力振荡,产生稳定的流场结构,并可有效降低空腔前缘的壁面热流值。
(2)由于空腔流场不产生周期性的压力振荡,因此参数L/D不影响空腔外形的气动力、热特性。
(3)空腔外形在有攻角状态时迎风面的前缘热流值会有所上升,但仍低于基准外形对应热流值;而背风面的热流会随攻角的增大有较大程度的降低。
(4)在4~7马赫范围内,空腔外形均可产生相对基准外形低30%左右的前缘壁面热流值。
[1]HARTMANN J,TROLL B.On a new method for the generation of sound waves[J].Physics Review,1922,20(6):719-727.
[2]BURBANK P B,STALLINGS R L.Heat-transfer and pressure measurements on a flat nose cylinder at a Mach number range of 2.49 to 4.44[R].NASA TM X -221,1959.
[3]JOHNSON R H.Instability in hypersonic flow about blunt bodies[J].The Physics of Fluids,1959,2(5):526 -532.
[4]BAYSAL O,STALLINGS R L.Computational and experimental investigation of cavity flow fields[J].AIAA Journal,1988,26(1):6-7.
[5]MARQUART E J,GRUBB J P.Bow shock dynamics of a forward-facing nose cavity[R].AIAA -1987 -2709,1987.
[6]HUEBNER L D,UTREJA L R.Experimental flow field measurements of a nose cavity configuration[R].Society of Automotive Engineers Paper 871880,1987.
[7]YUCEIL B,DOLLING D S,WILSON D.A preliminary investigation of the Helmholtz resonator concept for heat flux reduction[R].AIAA Paper 1993 -2742,1993.
[8]MILLER C G.Experimental and predicted heating distributions for biconics at incidence in air at Mach 10[R].NASA TP 2334,1984.
[9]KLOPFER G H,YEE H C.Viscous hypersonic shock-onshock interaction on blunt cowl lips[R].AIAA Paper 1988-0233,1988.
