来流边界层厚度对开式空腔气动声学特性的影响分析

杨党国，罗新福，李建强，蒋卫民

(中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000)

0 引言

空腔流动既是一个经典的流体力学问题，又广泛存在于航空航天领域。高速空腔流动，腔外剪切流与腔内流动相互作用，在一定条件下腔内出现流动自激振荡，诱发压力剧烈脉动，产生强烈噪声，噪声声压级可高达170dB，给腔内安装系统、储藏物与空腔自身结构安全带来了较大威胁［1］。

国外有人依据静压分布按长深比(L/D)不同将空腔大致分为三种主要流动类型，即闭式流动(L/D＞13)、过渡式流动(10≤L/D≤13)和开式流动(L/D＜10)［2－4］。对空腔声学特性也进行了一些试验研究，内容涵盖了亚跨超声速时腔内噪声测量与分析［5－8］。近年来采用数值模拟研究空腔声学特性的文献逐渐增多［9－10］。国内对此研究起步较晚，仅有的研究大多是采用数值方法［11－15］，试验研究相对较少，中国空气动力研究与发展中心高速所对空腔流动特性做了一些试验研究［16－17］。空腔声学特性复杂，目前在国际上对空腔自激振荡诱发噪声机理和影响因素解释仍未达成一致。本文着重分析了来流边界层厚度对开式空腔声学特性的影响。

1 试验模型

一期空腔模型L、W和D为80mm、56mm和10mm，直接安装在风洞侧壁上，试验中W和D不变，通过在空腔后端添加矩形堵块改变L，实现L/D变化。二期空腔模型L、W和 D为267mm、104mm和33.4mm，模型嵌套在平板上，平板安装在风洞侧壁上，试验中L和W不变，通过一个丝杠带动底板改变D，实现L/D变化。脉动压力测点均布置在空腔模型底面中心线上，试验照片见图1。

2 试验设备

试验风洞是中国空气动力研究与发展中心高速所的FL-21风洞。试验段横截面尺寸是0.6m×0.6m，长度为1.775m，风洞运行马赫数 Ma 范围是 0.3 ～4.0，跨声速时试验段上下为开孔壁，两侧为实壁;超声速时四壁均为实壁。脉动压力传感器是Endevco公司型号8514-10的压阻式传感器，固有频率为200kHz，量程为68kPa，名义灵敏度为4.35 ×10-3mV/Pa。

3 试验条件

试验迎角、侧滑角和滚转角均是0°，试验马赫数Ma为0.6 和 1.5，相应的雷诺数 Re分别是 1.23 ×107和2.26×107(参考长度1m)，空腔L/D为8。第一期试验在风洞侧壁试验段入口处、第二期试验在平板前缘粘贴金刚砂粗糙带进行人工转捩，粗糙带的宽度均为3mm。采用单点皮托管测量空腔试验模型前缘入口处的边界层厚度。

图1 风洞试验模型照片Fig.1 The photographs of the test models

4 数据处理

数据分析上限截止频率是1×104Hz，频域分辨率取4.88Hz，样本长度是1024，取32个样本作总体平均以减小随机误差。为减小因时域截断信号在频域产生的渗漏误差，数据处理加了海宁窗，并修正了加窗对声压频谱密度幅值的影响。此外，试验中信号调节放大系统选用0.1Hz高通滤波，对信号进行预处理，去除了信号中的直流成份。参数中SPL表示噪声声压级，斯托罗哈数(St=fL/U)是描述腔内流激振荡频率特性的一个无量纲参数。其中f指测的压力脉动频率，L是空腔长度，U是自由来流速度。

两期试验模型几何参数除宽深比W/D不同外，其余都相同。参考文献［3］研究结果指出W/D对空腔声学特性影响较小，因此相同Ma和L/D时，两期试验结果差异主要来自δ/D。δ/D具体参数见表1。

表1 边界层厚度与空腔深度比(δ/D)Table 1 The boundary-layer thickness to the cavity depth ratios(δ/D)

5 结果分析

5.1 亚声速流动条件

亚声速开式空腔流动，在空腔前壁为下台阶绕流，流动分离，一部分气流向腔内扩张，另一部分气流继续向腔后壁流动，并在空腔上方形成剪切层。剪切层运动到后壁前，流动再次分离，一部分气流移出空腔向下游运动，另一部分气流则沿着腔后壁向腔底面运动并穿过腔中部向前壁运动，在腔内形成连通腔前后部流动的旋涡(见图2)。这种流场结构导致剪切层与腔后壁相撞产生的强烈噪声能够通过连通腔前后部流动的旋涡传播至腔前壁，噪声能辐射到整个空腔区域。

Ma=0.6，不同δ/D时空腔内声压级分布基本相似。δ/D减小，腔内不同测点的声压级均有不同程度的增大，腔中前部测点表现较明显，如图3所示。从图4可知，δ/D减小引起空腔前部测点1不同离散频率对应的声压级均有不同程度的增大，且诱发较低频率区域(0.5＜St＜1.5)范围内出现了较明显的声压峰值激振频率;δ/D减小对空腔中部(测点2)和空腔后部(测点3)的声压频谱特性也有较大影响，导致不同离散频率对应的声压值明显增大，在低频区域同样也出现了声压峰值激振频率。

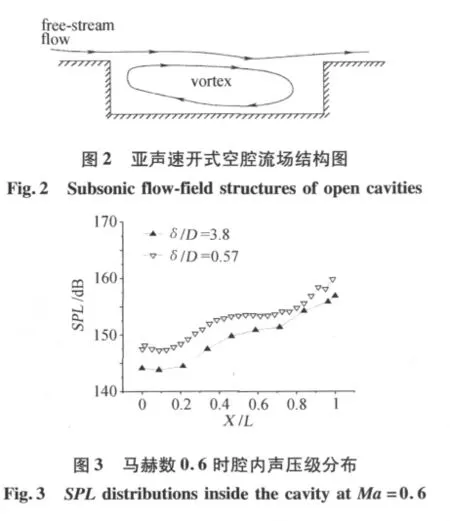
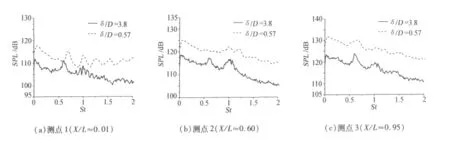
图4 马赫数0.6时腔内声压频谱特性Fig.4 Sound pressure frequency spectrum characteristics inside the cavity at Ma=0.6

引起开式空腔(Ma=0.6、L/D=8)声学特性发生上述变化的主要原因可能是δ/D减小(来流边界层厚度相对变小)，空腔上方形成的剪切层中的气流平均速度增大，剪切层与腔内流动作用的能量增加，引起剪切层更不稳定，诱发舱内噪声更强烈，故腔内不同测点的声压级均有不同程度的增大。

5.2 超声速流动条件

超声速开式空腔流动复杂，因腔长深比较小，气流流经腔前壁时微弱压缩，形成微弱压缩波或斜激波，气流压力升高、速度减小;随后流动发生分离，一部分气流向腔内扩张，另一部分在腔上方形成剪切层，剪切层从腔前壁出发，直接跨过腔中部，在腔后壁前流动再次分离，一部分气流沿空腔后壁通过腔底部向腔前壁运动，在腔内形成顺时针方向的旋涡，连通了腔前后部流动;剪切层与腔后壁相撞在空腔后壁处形成一道激波，如图5所示。

图6和图7给出Ma=1.5时L/D=8的空腔内声压级分布和声压频谱特性。气流在腔前壁微弱压缩后向腔内扩张，引起腔前壁后区域内声压级略微降低。空腔上方形成的剪切层跨过腔中部，与腔后壁碰撞，产生强烈噪声，引起腔内声压级从腔前壁单调递增至腔后壁处最大值(见图6)。不同δ/D时腔内声压级变化趋势基本相同。δ/D减小，腔内同一测点的声压级增大。δ/D减小，导致腔内第一测点(见图7a)和第二测点(见图7b)不同离散频率对应的声压级均有不同程度的增大，引起腔内激振频率略微偏移;导致第三测点(见图7c)在整个离散频率范围内声压级均有较大程度增大(特别是腔后壁附近最明显)。可见超声速(Ma=1.5)时，δ/D减小使开式空腔内噪声更强烈，同一测点相同离散频率对应的声压级增大。

引起开式空腔(Ma=1.5、L/D=8)声学特性发生上述变化的主要原因可能是δ/D减小，来流边界层内气流平均速度增大，导致腔前壁处压缩波或斜激波强度升高;空腔上方形成的剪切层与腔内流动相互作用的能量增加，导致腔内压力脉动加剧，故腔内不同测点的声压级均有较大程度的增大。

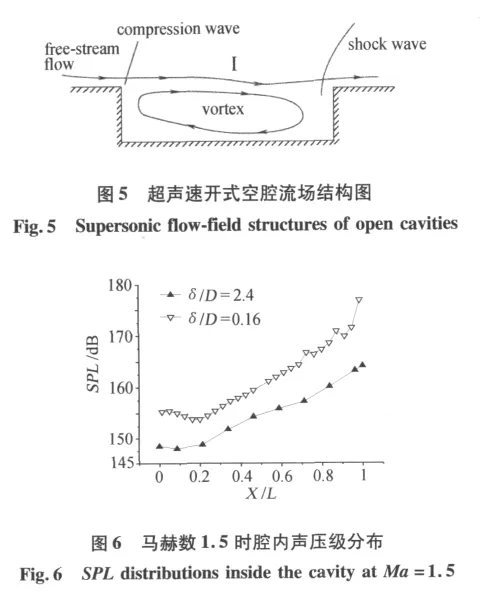
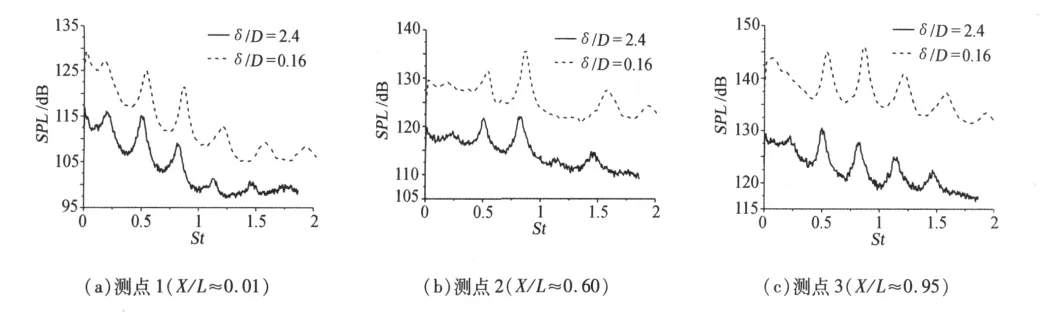
图7 马赫数1.5时腔内声压频谱特性Fig.7 Sound pressure frequency spectrum characteristics inside the cavity at Ma=1.5

6 结论

通过分析来流边界层厚度对开式空腔气动声学特性的影响，得出以下结论:

(1)δ/D减小(来流边界层厚度与空腔深度比减小)，导致开式空腔内不同测点的声压级均有不同程度增大，腔前后部的声压级分布更不均匀;

(2)δ/D减小，对开式空腔内不同测点的声压频谱特性有较大影响，主要引起同一测点不同离散频率对应的噪声声压级有不同程度增大，且声压峰值激振频率略微偏移;

总之，δ/D减小导致开式空腔内噪声更强烈，更易引起空腔自身结构与腔内储藏物结构振动和疲劳破坏。

［1］LAI H，LUO K H.A three-dimensional hybrid LES-acoustic analogy method for predicting open cavity noise［J］.F1ow，Turbulence and Combustion，2007，79(1):55－82

［2］SHAW L L，et al.F-111 generic weapons bay acoustic environment［R］.AIAA 1987 －0168.

［3］CHING-WEI M S，PHILIP J M.Comparison of two and three-dimensional turbulent cavity flows［R］.AIAA 2001 －0511.

［4］ROBERT L，STALLINGS Jr and FLOYD J，WILCOX Jr.Experimental cavity pressure distributions at supersonic speeds［R］，NASA Technical Paper－2683，1987.

［5］PLENTOVICH E B，ROBERT L，STALLINGS，Jr.and TRACY M B.Experimental cavity pressure measurements at subsonic and transonic speeds［R］.NASA Technical Paper－3358，1993.

［6］STALLINGS，ROBERT L Jr and FORREST DANA K.Separation characteristics of internally carried stores at supersonic speeds［R］.NASA-TP-2993，1990.

［7］WILCOX，FLOYD Jr.Experimental investigation of porousfloor effects on cavity flow fields at supersonic speeds［R］.NASA-TP-3032，1990.

［8］ABRABAM J.An experimental study of open cavity flows at low subsonic speeds［R］.AIAA 2002 －0280.

［9］HAMED，D BASU and K DAS.Detached eddy simulations of supersonic flow over cavity［R］.AIAA 2003 －549.

［10］LAWRENCE UKEILEY，et al.Velocity and surface pressure measurements in an open cavity［J］.Experiments in Fluids.2005，38:656 －671.

［11］司海青，王同光，宗慧英.腔内平板对空腔自激励振荡的影响及预估振荡频率方程的改进［J］.航空动力学报，2006，21(6):1037－1042.

［12］李晓东，刘靖东，高军辉.空腔流激振荡发声的数值模拟研究［J］.力学学报，2006，38(5):599－604.

［13］肖虹，高超，党云卿.飞行器腹部空腔绕流的数值模拟［J］.航空计算技术，2007，37(4):44－46.

［14］张强.流动诱导空腔振荡频率方程的改进［J］.振动工程学报，2004，17(1):53－57.

［15］罗柏华.二维高亚声速空腔流激振荡的数值模拟研究［J］.空气动力学学报，2002，20(1):84－88.

［16］杨党国，范召林，李建强，罗新福.弹腔流动特性数值模拟及风洞试验研究［J］.空气动力学学报，2008，27(3):378－383.