ARIMA模型在居民消费价格指数预测中的应用
2011-11-07辛海明
辛海明
(中山大学 新华学院,广东广州 510520)
ARIMA模型在居民消费价格指数预测中的应用
辛海明
(中山大学 新华学院,广东广州 510520)
本文以我国 2001~2009年月季度的消费价格指数为例,通过 SAS软件对 AR IMA模型进行拟合预测,结果表明该模型有效,预测值精度较高。
时间序列;AR IMA;CPI
近年来,由权威机构数据表明,受国际商品价格的上涨,国内市场需求旺盛,全国居民消费指数(CPI)持续上涨。CPI指数反应通货膨胀的程度,通常作为观察通货膨胀水平的重要指标。很多模型都可以用来预测 CPI,比如说线性回归模型LRM,该模型只能拟合预测数据呈线性趋势的情况,对数据呈非线性的情况基本无效。还有 ARMA模型,该模型也能进行预测,但使用条件较为苛刻,要求数据要满足平稳性,对带有趋势效应和周期效应的数据束手无策,而AR IMA模型能处理呈非线性、周期性的数据,因而适用范围较更广。因此,运用AR IMA模型对我国 CPI指数进行预测是比较合适的。
本文通过分析 2001~2009年的居民消费价格指数数据建立 AR IMA模型,对 2010年 1月至9月 CPI的走势进行数据上的验证,并预测 2010年 10月至 12月 CPI的走势。
一、时间序列基本理论与方法
时间序列分析方法有很多,最初的ARMA(p,q)模型只能处理平稳非白噪声序列,具体形式如下:
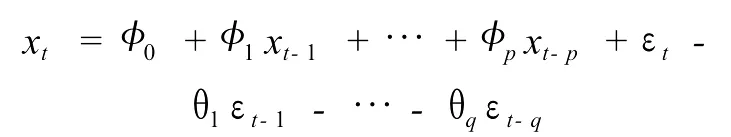
引进延迟算子,ARMA(p,q)模型简记为:
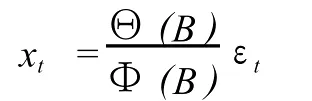
其中Φ(B)=1-φ1B-…-φpBp为p阶自回归系数多项式,Θ(B)=1-θ1B-…-φpBp为q自回归多项式,εt为白噪声序列。实际中得到的数据常常是非平稳的,但对非平稳原序列进行差分后可以得到平稳序列,所以常用的模型为简记为ARMA(p,d,q),d为差分阶数。
二、验证原始数据的平稳性
下面以我国 2001年 (1月 -12月)~2009年(1月 -12月 )居民消费价格指数 (上年同月:100)的数据 (数据来源:中经网统计数据库)为例建立模型并检验。
编写 SAS程序对原数据进行平稳性、随机性检验,试验结果如下:
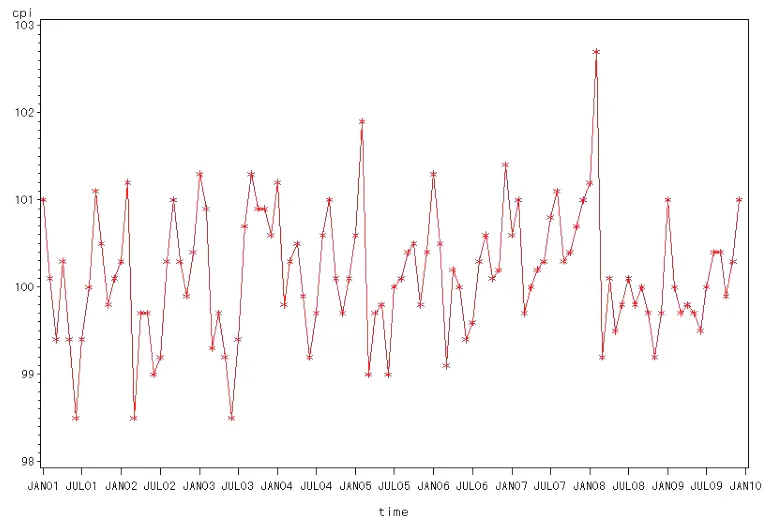
图1 原始数据的时间序列变化
从图1可知,原始序列似乎平稳,但从原始序列的自相关和偏自相关系数可以看出 (如表 1),原始数据存在明显的周期性,且周期为 12,由此可判断数据不平稳,有着自相关性。
为了进一步检验原始序列是否平稳,需对原始数据进行 ADF检验。通过表 2可知,原始序列的 ADF检验的概率在 5%水平下 (零均值)不能通过检验,因此原序列非平稳。
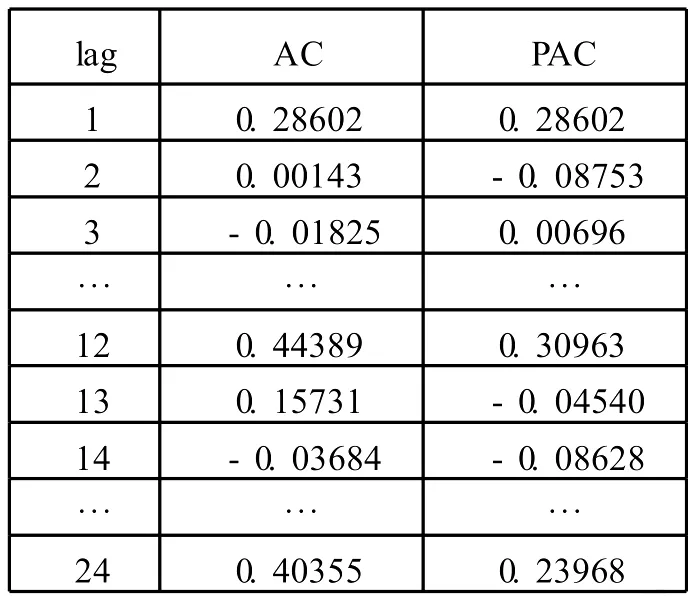
表1 原始数据自相关和偏自相关系数
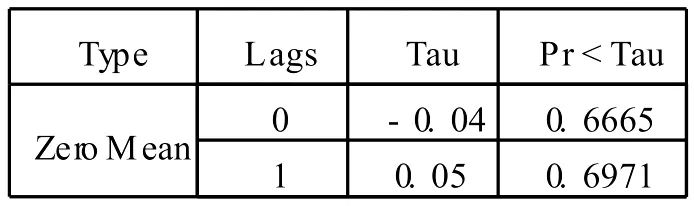
表2 原序列 (CPI)单位根检验
由序列白噪声检验 (如表 3)可知,原序列可视为非纯随机序列。
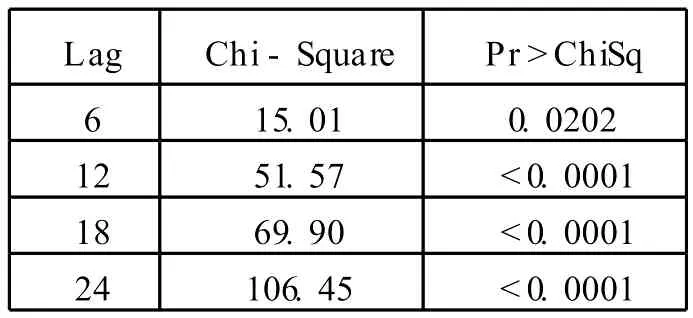
表3 原序列白噪声检验
三、建立 AR IMA模型
通过 SAS软件中得出的检验结果可知,原序列有步长为 12的周期性,因此对 12步差分改进后的时间序列进行平稳性和纯随机性检验,结果如表 4、表 5所示,差分后的序列 D12CPI为平稳非白噪声序列,因此可以进行时间序列分析。根据 12步差分后的自相关图和偏自相关图如图 2、图 3所示,可以建立模型:
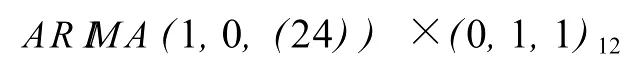
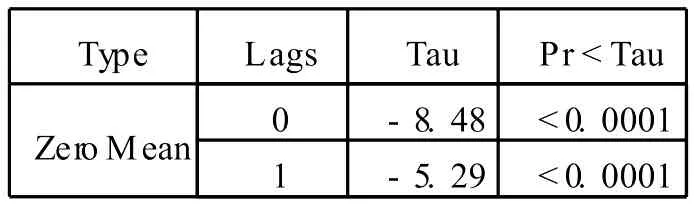
表4 12步差分后 (D12CPI)单位根检验
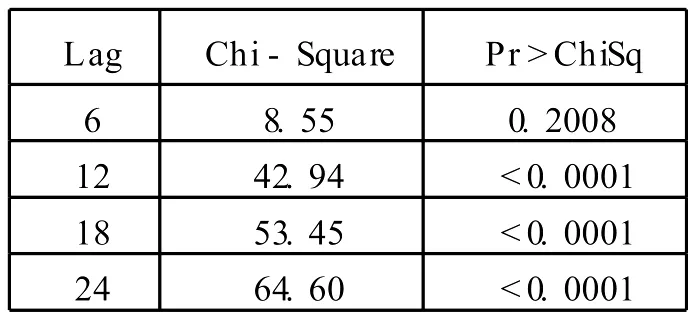
表5 12步差分后 (D12CPI)白噪声检验

图2 差分后序列 D12CP自相关图
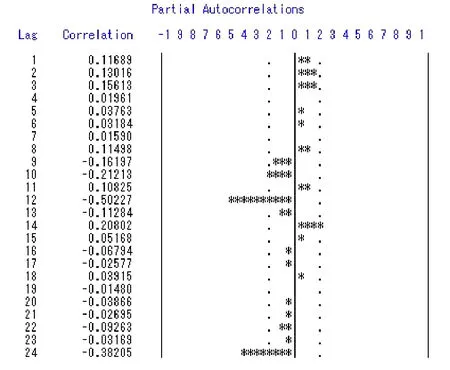
图3 差分后序列 D12CP自相关图
四、模型检验和预测
由表 6的输出结果可以看出,除 AR1,1的估计值不显著外,其余参数均显著,表 7结果显示该模型顺利通过残差白噪声检验。因此最终模型为:
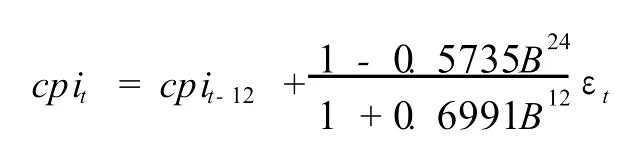
即AR I MA(0,0,(24))×(0,1,1)12
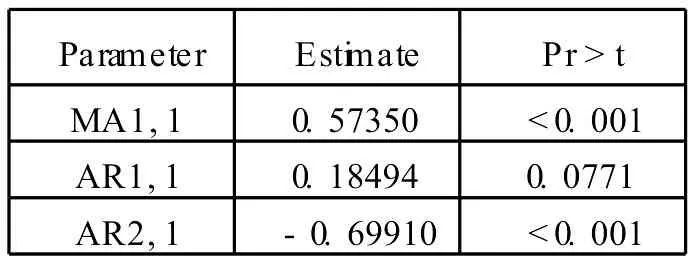
表6 参数估计值及检验
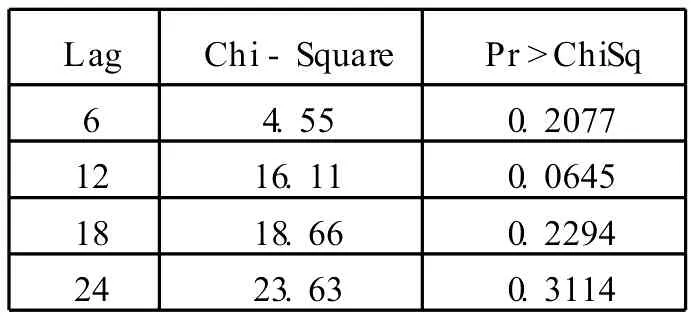
表7 残差白噪声检验
为检验模型预测的效果,以我国 2010年 1月-9月份的居民消费价格为参照对象,结果如表 8所示:
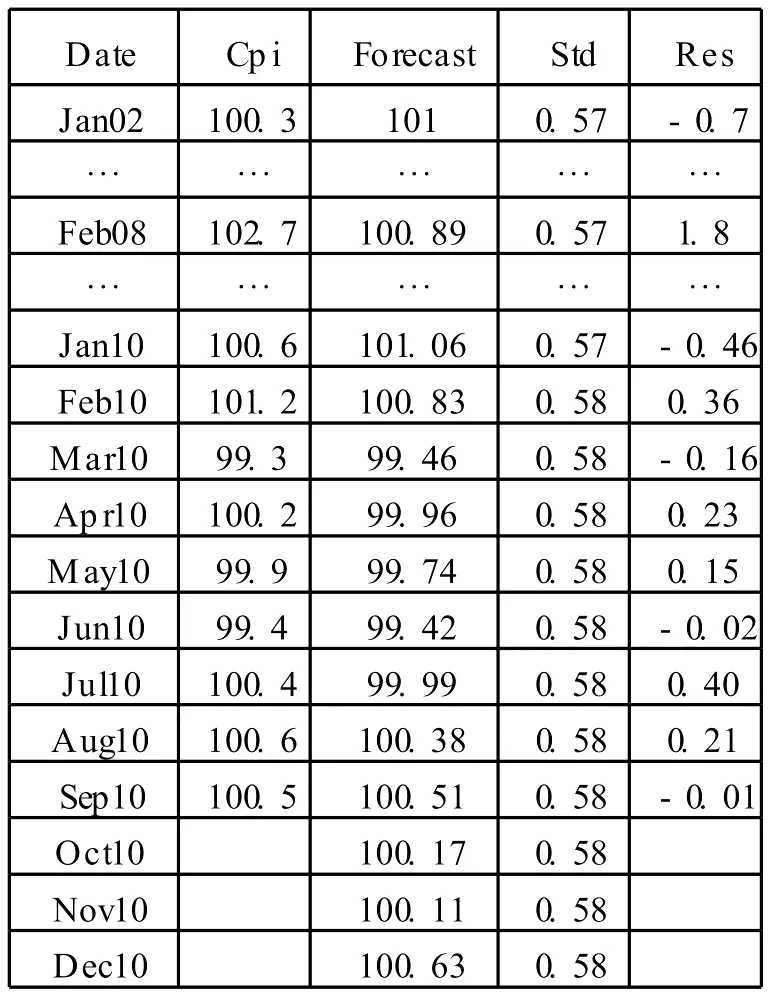
表8 AR IMA模型的 CPI预测结果
根据预测结果 (表 8)可以看到,预测到的指数与实际数据相差很小,虽然有些时间点上的实际值和预测值相差比较大,例如 Feb08实际值是102.7,预测值是 100.89,误差相对较大,但那是因为 Feb08发生了雪灾,居民消费受到了非随机因素的影响,从而误差较大。总体来说该模型对预测消费价格指数是比较有效的。
由以上实证分析可知,预测值的相对误差较小,模型的效果较好。因此,可以利用该模型预测未来消费价格指数的变化规律。但是AR I MA(0,0,(24))×(0,1,1)12模型也有它的局限性,如在使用AR IMA模型时我们只检验了残差的自相关性,只要白噪声检验通过了就认为模型通过检验并可以使用了,在这过程中其实是假定了残差是同方差的,但实际中残差却经常是异方差的,这会影响拟合精度,不能很好地进行数据预测。此外,目前AR IMA模型基本上都是在经济、金融领域中应用,它在其它领域的应用还有待进一步发掘。
[1]王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005.
[2]黄燕,吴平.SAS统计分析及应用 [M].北京:机械工业出版社,2007.
[3][美 ]沃尔特.恩德斯.应用计量经济学时间序列分析(第二版)[M].北京:高等教育出版社.1999.
[4]郝冉.居民存款余额的时间序列分析 [J].统计与决策,2007,(19).
[5]刘春燕,姚杰.时间序列分析在居民消费价格指数预测中的应用[J].现代商贸工业,2010,(16).
F015
A
1003-8078(2011)02-147-03
2011-01-17
10.3969/j.issn.1003-8078.2011.02.45
辛海明 (1983-),男,湖北黄石人,中山大学新华学院助教,硕士。
责任编辑 周觅
