Cauchy积分公式及其导数公式证明在数学物理方法教学中的探讨

赵玉杰 ，李 李 ，余春日

（安庆师范学院 a.物理与电气工程学院；b.文学院,安徽 安庆 246011）

Cauchy积分公式及其导数公式证明在数学物理方法教学中的探讨

赵玉杰a，李 李b，余春日a

（安庆师范学院 a.物理与电气工程学院；b.文学院,安徽 安庆 246011）

本文利用实变函数积分中值定理，并结合Cauchy积分定理在复围线推广形式，用实变函数积分的方法证明了复变函数论中的积分公式。并用复变函数求导函数的方法和数学归纳法证明了Cauchy型积分导数公式。证明过程简单易懂。

Cauchy积分公式；Cauchy积分定理；解析函数；数学物理方法；高阶导数

Cauchy积分公式是复变函数论的重要公式之一。其重要性主要体现在：给出了解析函数的积分表达形式，即函f(z)数在围线C内任一点z0处的函数值f(z0)可由函数沿围线C的积分来表示。正是由于这一点，Cauchy积分公式提供了计算复积分的重要方法，它把沿围线的积分转化为求函数的函数值，从而简单巧妙地解决了大量复积分的计算问题。关于Cauchy积分公式及导数公式的证明，许多参考书和文献都涉及到[1－3]，其方法大都是从复变函数极限或导数的定义出发，证明虽然比较严谨，但过程较为繁琐，在数学物理方法课程教学中，如果仅用此方法推导证明，往往难以理解。为此，我们尝试在Cauchy积分公式证明中，将实变积分的积分中值定理，应用到复变函数积分，将复变积分问题，转化为实变积分。对Cauchy型高阶导数公式的证明，我们采用复变函数求导方法，并进行归纳，最后利用数学归纳法证明之。通过上述方法，Cauchy积分公式及其导数公式均得到了很好的证明，证明过程简单易懂。

1 Cauchy积分公式[1-3]

定理一(Cauchy积分公式)：设围线C为区域D的边界，f(z)在=D+C上解析，则对于区域D内任一点 z，有：

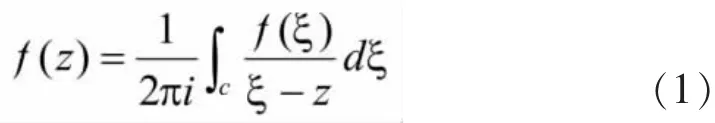
在利用新的证明方法之前,我们先给出本文所用到的定理和公式。

2 Cauchy积分公式的证明

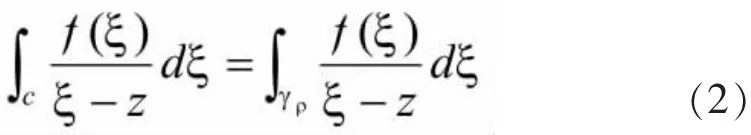
对于（2）式的右端，积分变量是ξ，z相对固定；且右端的积分值与γρ的半径ρ的大小无关，即

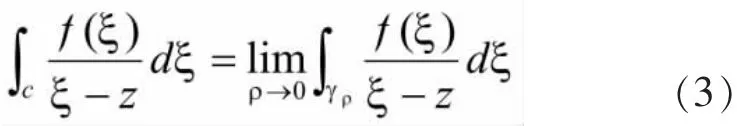
因此我们只要证明

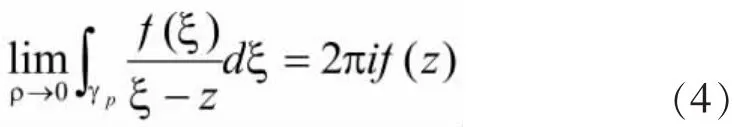
就可以了。

对于（4）式左端，采用换元法，将复积分变为实积分。

令 ξ=z+ρеiθ， （0≤θ≤2π）

则 dξ=iρеiθdθ

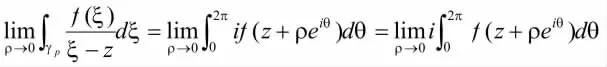
上式中被积函数 f（z+ρеiθ）属于实变复值函数，

且 f（z+ρеiθ）=Ref（z+ρеiθ）+iImf（z+ρеiθ）

对被积函数 f（z+ρеiθ）的实部与虚部分别利用积分中值定理：

在[0，2π]上，点 ζ1，ζ2∈[0,2π]使得

3 Cauchy高阶导数公式[1-3]

定理二(Gauchy高阶导数公式)：设围线C为区域D的边界，f(z)在=D+C上解析，则f(z)区域D内有任何阶导数f(n)(z)均存在，且

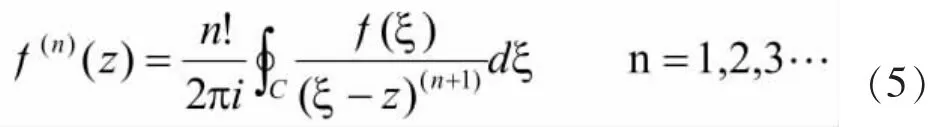
4 Cauchy高价导数公式的证明

分析：利用复变函数直接求导的方法，对的表达式（公式），分别求出的一、二阶导数 f'(z)，f''(z)，然后根据前三项的规律，归纳出f(z)的n阶导数，最后用数学归纳法证明之。

证明：由于函数f(z)对z求导时，与公式（1）中的积分变量ξ无关，因此求导时，将ξ看成常量。将Cauchy积分公式（1）在积分号下对z求导，可得：

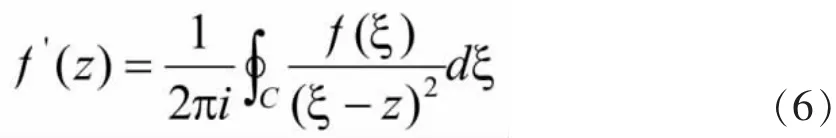
对（6）式继续对求导可得

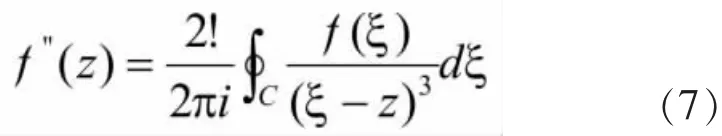
再对（7）式对继续求导可得

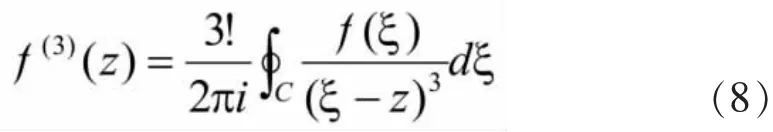
根据前面对求f(z)求一、二、三阶导数的结果，我们可归纳出f(z)的阶导数f(n)z公式为

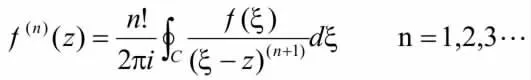
现在用数学归纳法证明之：

但n=1时，由（6）式可知，显然成立。

令 n=k 时，（5）式成立，即

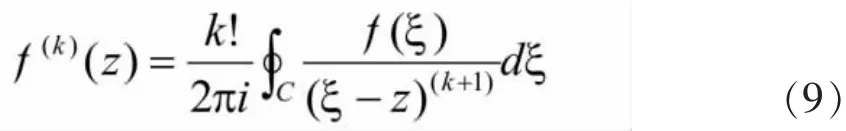
将（9）式对 z求一次导，得

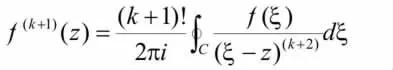
即n=k+1时，也成立。

故定理二成立。即

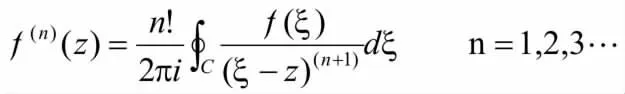
在讲解高阶导数公式时，我们首先采用对Cauchy积分公式求导的方法来得到这一公式，然后用数学归纳法证明。虽然这种做法在数学上不够严谨的，但能帮助初学者熟悉和把握高阶导数公式。

5 结论

本文通过利用实积分的方法对Cauchy积分公式的证明,并利用复变函数直接求导和数学归纳法,证明了Cauchy型积分高阶导数公式公式。

[1]四川大学数学系.高等数学：第四册[M].北京：高等教育出版社,1985.

[2]钟玉泉.复变函数论[M].2版.北京:高等教育出版社，2002.

[3]吴崇试，数学物理方法[M].2版.北京：北京大学出版社，2003.

[4]同济大学应用数学系，高等数学:上[M].北京：高等教育出版社,2002.

O175

A

1674-1102(2011)03-0038-02

2011－04－25

安徽高校省级自然科学研究重点项目（KJ2010A227）。

赵玉杰(1975－)，男，安徽安庆人，安庆师范学院物理与电气工程学院讲师,中国科学技术大学博士，研究方向为数学物理方程教学。

[责任编辑：桂传友]