基于最小二乘回归模型的EIT数据分析

侯 雪，刘 準

(1.天津轻工职业技术学院 电子信息与自动化系，天津 300122;2.天津电力工程监理有限公司，天津 300122)

基于最小二乘回归模型的EIT数据分析

侯 雪，刘 準

(1.天津轻工职业技术学院 电子信息与自动化系，天津 300122;2.天津电力工程监理有限公司，天津 300122)

医学电阻抗成像技术(EIT)是当今生物医学工程领域重大研究课题之一。本文利用最小二乘回归模型分析了圆形场EIT扫描数据，实现了场域内干扰物质的相对尺寸及相对位置的确定，为实现EIT动态心肺监测活动奠定基础。

医学电阻抗成像技术;最小二乘回归模型;心肺监测

0 引言

医学电阻抗成像技术 (EIT-Electrica1 Impedance Tomography)是当今生物医学工程领域重大研究课题之一。EIT技术根据物体内部组织电特性参数不同，通过对其表面施加安全激励电流，测量响应电压，然后根据测量数据，重建电阻抗分布图像。EIT技术应用于动态监测心肺活动的过程中，确定心脏、肺部的相对尺寸及相对位置是很重要的。本文通过圆形场仿真实验，利用最小二乘回归模型方法分析其EIT数据，进而确定干扰相对位置及相对尺寸。以此仿真实验为例说明EIT技术在确定心肺尺寸及位置方面的应用。

1 回归模型及分析方法简介

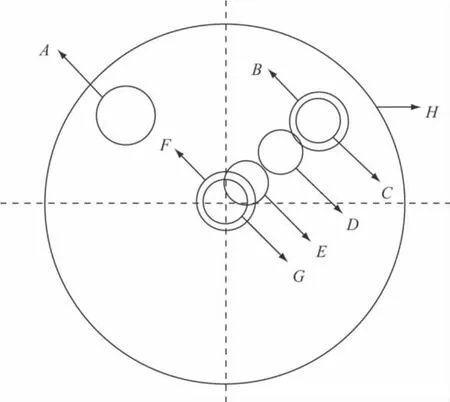
图1 八种不同干扰情况具体分布

首先，建立圆形空场仿真模型，分别设置八种不同位置、不同尺寸的干扰。然后分别对八种情况进行EIT仿真及回归模型分析，最后由数据分析结果确定干扰相对位置及尺寸。仿真过程中，空场介质电导率设置为80S/m，干扰介质电导率均设置为1S/m。八种干扰情况如图1、表1所示:

表1 八种不同干扰尺寸及分布情况

2 回归算法简介

圆形场仿真模型周围设16个电极，采用相邻电极循环激励的激励方式，每次激励测量所有相邻电极电压。首先按照图2的步骤对所得方阵进行相关处理，然后按照下述方法求得电压序列［E］i电压序列［E］i的求法如下:

图2 回归算法示意图

3 数据采集与分析

4 以空场情况为参考的数据分析

首先确定干扰是否与圆形场同轴。应用回归模型方法处理测量电压数据。如果测量数据以空场情况H为参考，所得电压序列图像斜率恒定，则说明干扰与空场模型同轴。从另一个角度来看，同心扰动所生成的曲线大致平行。确定扰动的性质(同心或偏心)后，下一步就是判断干扰的偏心程度及干扰尺寸。观察偏心情况电压序列图像，通过图像位置上下关系即可确定偏心程度。以空场情况为参考求得电压序列矩阵，通过求解该矩阵各个元素的平方和可以比较并确定干扰的相对尺寸。这种方法可以使用于同心及偏心各种情况。相对尺寸计算公式为:

以空场情况为参考进行同轴，偏心情况相关数据及图像分析。

eah代表以情况H为参考，干扰A数据图像。ebh代表以情况H为参考，干扰B数据图像。ech代表以情况H为参考，干扰C数据图像。edh代表以情况H为参考，干扰D数据图像。eeh代表以情况H为参考，干扰E数据图像。efh代表以情况H为参考，干扰F数据图像。egh代表以情况H为参考，干扰G数据图像。ehh代表以情况H为参考，干扰H数据图像，见图3～图4。

图3 同轴与偏心情况对比(以情况H作为参考)

图4 同轴与偏心情况对比(以情况H作为参考放大图像)

通过图3及图4可以看出，干扰F为同轴干扰，其图像斜率基本恒定，并平行于空场情况;干扰A、B处于偏心状态，其图像斜率有一变化过程。但由于干扰A位于第二象限，干扰B位于第一象限，二者相对位置不同，所以图像斜率变化过程所处帧位置不同，A干扰的图像滞后于B干扰。

图5 同轴情况对比(以情况H作为参考)

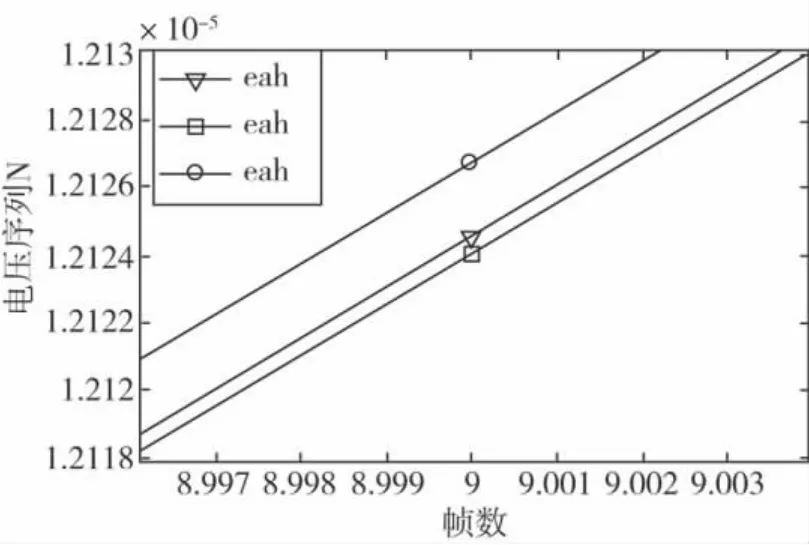
图6 同轴情况对比(以情况H作为参考放大图像)

通过图5及图6可以看出，干扰F及干扰G均为与实验容器同轴的干扰，它们的图像均基本平行于空场情况，并彼此基本平行，体现了干扰的对称性。干扰F、G均处于空场图像之下，干扰F的尺寸大于干扰G，其图像位于干扰G的图像之上。

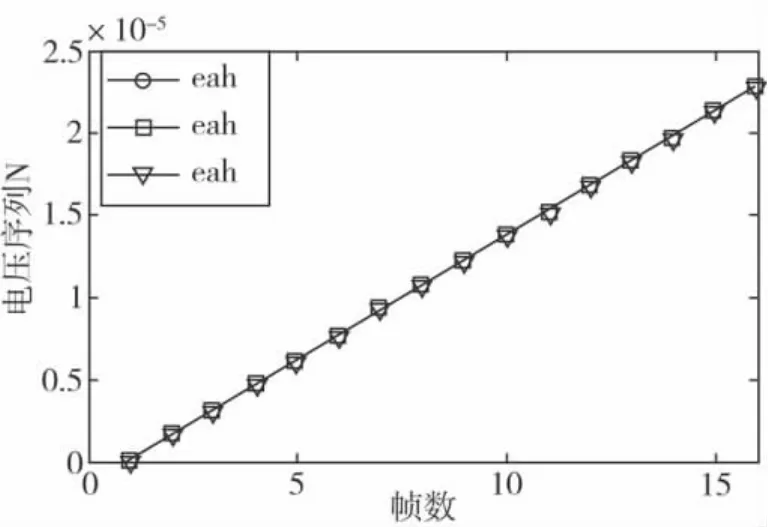
图7 偏心程度对比(以情况H作为参考)

图8 偏心程度对比(放大图像)(以情况H作为参考)

干扰C、D、E为尺寸相同偏心位移沿第一象限角平分线依次减小的偏心干扰，由图7及图8可见，三者图像基本平行。随着偏心位移的减小，图像依次向下平移。

干扰B、C圆心处于同一位置、偏心程度相同、尺寸不同，由图9可见，二者图不完全平行，尺寸较大的干扰B的图像位于较小尺寸干扰C图像之上。

5 结论

图9 偏心尺寸对比(以情况H作为参考)

以空场为参考时，与容器同轴的干扰斜率基本恒定并彼此平行;其图像均位于空场图像之下，尺寸较小的同轴干扰图像位于尺寸较大的同轴干扰图像之下。偏心干扰与空场图像不平行，相同尺寸不同偏心程度的干扰图像彼此近似平行，随着偏心位移的减小，其图像依次下移;相同偏心程度不同尺寸的偏心干扰其图像部分平行，大尺寸偏心干扰图像位于小尺寸偏心干扰图像之上;同尺寸不同象限的偏心干扰图像可以通过图像平移互化，后一象限的干扰图像滞后于前一象限的干扰图像。

综上所述，利用最小二乘法回归模型处理EIT数据后，通过对其数据对应图像的分析，均可以迅速推测出干扰的相对尺寸及相对位置。

［1］董秀珍.生物电阻抗技术进展［J］.常规医疗装备，2004，3(4):34－38.

［2］唐化勇，牟永阁，杨常运.生物电阻抗成像技术在医学中的应用［J］.第四军医大学吉林军医学院学报，2000，22(3):174－176.

［3］倪光正，杨仕友，等.工程电磁场数值计算［M］.北京:机械工业出版社，2004.

［4］邓娟，任超世.EIT图像重建算法的进展研究［J］.中国医学装备，2007，4(6):1－5.

［5］董秀珍.生物电阻抗成像研究的现状与挑战［J］.中国生物医学工程学报，2008，27(5):641－649.

责任编辑:钟 声

EIT data analysis based onleast square regression model

HOU Xue，LIU Zhun
(1.Department of Electronic Information and Automation，Tianjin Light Industry Technical College，Tianjin 300122，China;2.Tianjin Electric Power Engineering Supervision Co.，Ltd，Tianjin 300122，China)

Medical electrical impedance tomography technology(EIT)is an important subject in biomedical engineering field.This paper analyzes the circular field EIT scan data by using least square regression model and achieves the determination to the relative size and position of interfering substances within the field，which provides foundations for EIT dynamic cardiopulmonary monitoring activities.

medical electrical impedance tomography technology(EIT);least square regression model;cardiopulmonary monitoring

O241

A

1009－3907(2011)06－0055－03

2011-03-15

侯雪(1981-)，女，吉林长春人，讲师，主要从事自动化控制与检测方面研究。