未预期模型误差影响下秩减估计器的性能分析

王鼎，吴瑛

（信息工程大学 信息工程学院，河南 郑州 450002）

1 引言

众所周知，高分辨率算法往往受阵列误差的影响较大，因此阵列误差校正技术一直是国内外研究的热点问题。关于阵列误差校正方法主要分为两大类：第一类是有源校正方法[1,2]，即利用方位已知的校正源对阵列误差参数进行离线估计，该类方法虽然对算法的实时性要求较低，但对校正源的方位精度有较高要求；第二类是自校正方法[3,4]，该类方法通常将信源方位和阵列误差参数根据某种准则进行联合优化，可在估计信源方位的同时完成阵列误差的自校正，并不需要方位已知的校正源，但其中联合估计对应的高维、多模非线性优化会带来庞大的运算量，从而使得算法的实时性和稳健性较差，全局收敛性难以保证。

为了避免阵列误差自校正方法中存在的上述问题，一类所谓“秩减估计器(RARE, rank reduction estimation)[5～12]”引起了学者们的关注，这是因为RARE可在无需已知(预期)阵列误差的条件下估计信源方位，基于信源方位的准确估计又可完成预期阵列误差的精确自校正，从而能够避免迭代运算和局部收敛等问题。例如，文献[5,6]针对均匀线阵和均匀圆阵互耦矩阵的Toeplitz模型，提出了一种互耦自校正的RARE；文献[7]提出了一种累量域互耦自校正的RARE；文献[8,9]通过均匀圆阵的模式空间转换及其互耦特性提出了一种可用于估计信源二维来向的 RARE；文献[10]利用精确校正的辅助阵元提出了一种可用于校正“方位依赖幅相误差”的 RARE；文献[11,12]提出了一种可用于校正多子阵部分阵列误差的RARE等。当(预期)阵列误差模型满足RARE要求时，上述方法都能取得较好效果，然而实际中可能存在一些未预期模型误差会破坏RARE的数学模型，从而影响其参数估计精度。例如，文献[5,6]中的均匀阵列可能存在幅相误差，并且实际中互耦矩阵可能在Toeplitz矩阵的基础上发生微弱扰动[13]；文献[7]中的累量域互耦矩阵模型同样存在上述问题；文献[8,9]对均匀圆阵进行模式空间转换也会带来一定偏差[14]；文献[10]中精确校正的辅助阵元也可能存在小的幅相误差；文献[11,12]多子阵中各个子阵的标称方向可能存在小的扰动偏差[15]等。上述模型误差都是在 RARE中所忽略的，文中将其称为“未预期的模型误差”。针对RARE中存在的未预期模型误差，从理论上定量分析了RARE的方位估计性能，分别推导了RARE的方位估计均方误差和高斯误差模型下的测向成功概率。最后针对一种用于均匀阵列互耦自校正的RARE给出了数值实验，用来验证文中理论推导的有效性。

2 常用符号定义和预备数学知识

2.1 常用符号定义

为了便于文中的理论分析，这里给出一些符号定义：① d et［⋅］表示矩阵行列式；②［⋅］†表示矩阵Moore-Penrose逆；③vec(⋅)表示矩阵向量化算子；④ d iag［⋅］表示由向量中的元素构成的对角矩阵，bdiag［⋅］表示由矩阵或向量作为对角元素构成的块状对角矩阵；⑤ In表示n阶单位矩阵，其中第i列向量为 ei(n)；⑥Re{⋅}和Im{⋅}分别表示取实部和虚部；⑦δkl表示delta函数，若k=l，则δkl=1，否则 δkl=0；⑧χ2(n)表示自由度为n的卡方分布；⑨ G (μ，R)表示均值(向量)为μ，方差(矩阵)为R的高斯分布。

2.2 预备数学知识

引理1[16]设随机向量 x ～χ2(n)，则其特征函数为 φx(t)=(1 -2 it)-n2。

在引理1的基础上可以得到如下结论。

命题1 设实随机向量 ε ～ G ( 0 ， Rε)，其中Rε是正定矩阵，令H为半正定矩阵，并且满足rank[H]=N，假设矩阵的N个正特征值分别为 λ1,λ2, …,λN，则二次型y=εTHε的特征函数为

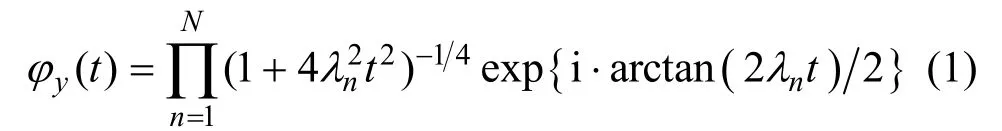
证明见附录A，命题1对于推导RARE的测向成功概率起着非常关键的作用。

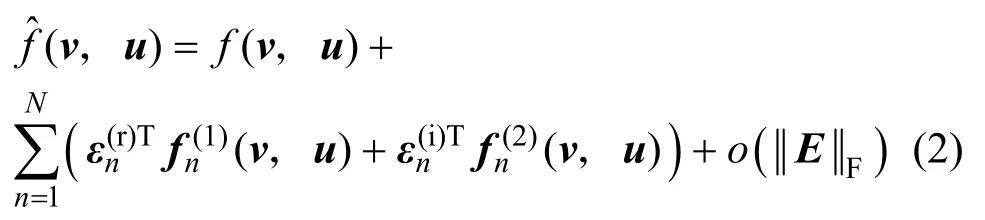
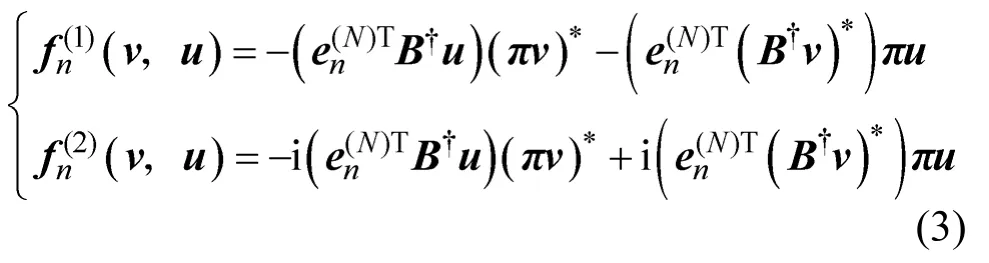
证明见附录B。基于命题2可得如下结论。

推论 1 设 uk，vk∈ CM×1（k= 1，2，…，K），其余符号同命题2，则有

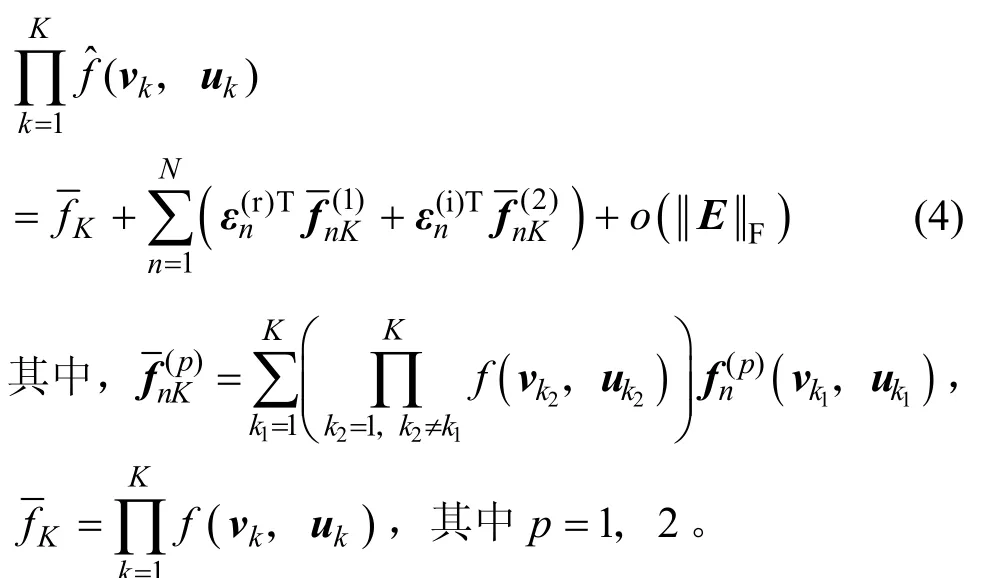
证明见附录C，推论1对于推导RARE的方位估计偏差起着非常关键的作用。

3 阵列信号模型和秩减估计器

现有一个M元阵列，其阵列流型中存在着阵列误差，并且这种阵列误差可分为2部分：第一部分是预期但未知的阵列误差，并且其数学模型满足RARE的要求；另一部分则是未预期且未知的模型误差，在大样本或高信噪比条件下它是影响RARE性能的主要因素。现在阵列远场处有N个窄带信源以平面波的方式入射，则阵列的输出可表示为

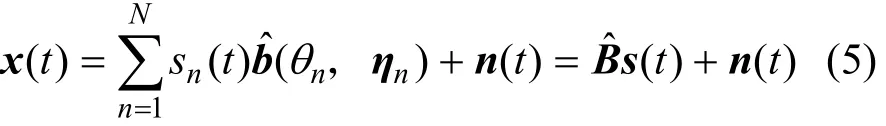
其中，n（t）为复圆高斯白噪声，s(t)为信源复包络，Bˆ=[bˆ（θ1，η1）bˆ（θ2，η2）…bˆ（θN，ηN）]为阵列方向矩阵，其中， bˆ （θn，ηn）为阵列流型向量，这里不妨将其表示为

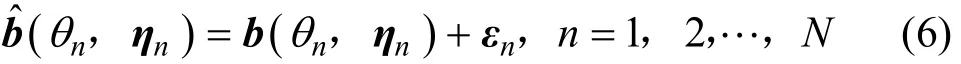
其中，b（θn，ηn）用来表示预期的阵列流型向量，θn表示第n个信源的方位，ηn用来刻画预期但未知的阵列误差参数。为了满足RARE的要求，b(θ，η)通常满足如下等式

式中矩阵 T(θ ) ∈ CM×K仅与方位θ有关，这里不妨将其按列分块表示为 T(θ ) = ［t1(θ )t2( θ)…tK(θ)］，而Φ （θ ,η ） ∈ CK×1表示包含预期阵列误差参数的列向量。为了满足RARE参数估计唯一性要求，还需要满足条件K≤M-N。需要指出的是，在不同的应用背景下， Φ （θ， η）既可以是同时关于θ和η的函数[10～12]，也可以是仅关于 η 的函数[5～7]。另一方面，式(6)中的向量εn则表示未预期且未知的模型误差，对于不同的误差模型，误差向量εn的表示形式不同。

根据式(6)可将阵列方向矩阵表示为Bˆ=B +E ，其中B=[b（θ1，η1） b （ θ2，η2）…b（θN，ηN）]表示预期的方向矩阵，而E=［ε1ε2…εN］表示未预期的模型误差矩阵。根据式(5)可得阵列协方差矩阵为

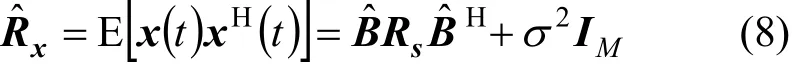
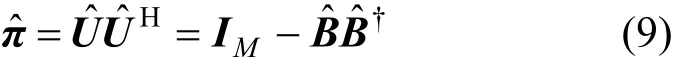
于是可得RARE的空域谱为

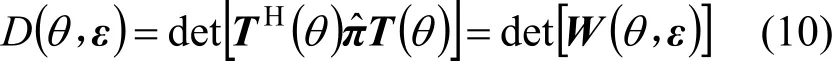
其中，ε表示由未预期模型误差构成的实向量，它的表示形式为和εi=Im｛v ec (E)｝。由于式(10)中的πˆ是受到未预期模型误差扰动的正交投影矩阵，这必然会影响RARE的方位估计性能，下文将从方位估计均方误差和测向成功概率2个角度对其进行研究，并推导相应的理论表达式。事实上，MUSIC算法也可以看作是一种特殊的RARE，只是其中的K取1，所以文中的结论也可应用于MUSIC算法。

4 秩减估计器的方位估计均方误差

本节将推导RARE的方位估计均方误差，为此需要首先推导 RARE的方位估计偏差。由于文中的RARE是针对预期阵列误差的自校正方法，因此这里假设未预期的模型误差不会影响一阶误差分析方法的精度，并且ε是服从零均值的高斯分布。首先记wij（θ，ε）=tiH（θ）πˆtj（θ），则有W（θ，ε） =（ wij（θ，ε）K×K，于是根据矩阵行列式的定义可得

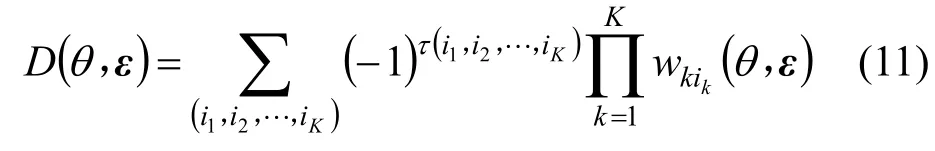
其中， τ（i1， i2，…，iK）表示排列（i1， i2，…，iK）的逆序数，累加号表示对1，2，…，K的一切排列求和，它共有K ! 项构成。若令D˙（θ，ε）=∂D（θ，ε ）∂θ，则根据式(11)可得：

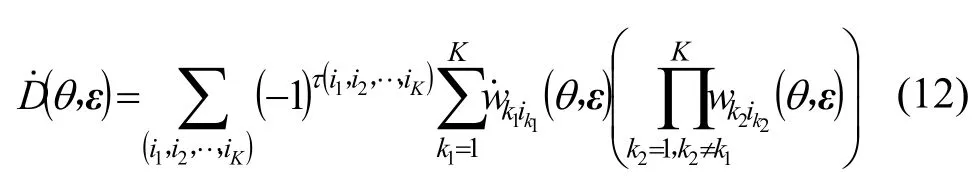
其中，w˙ki（θ，ε）=∂ wki（θ，ε）∂θ。假设θˆm是对应于kk真实方位θm的估计值，则有D˙（θˆm，ε）=D˙（θm，0）=0，当θˆm与θm足够接近，并且ε中的元素足够小时，利用一阶Taylor级数展开可得如下近似等式

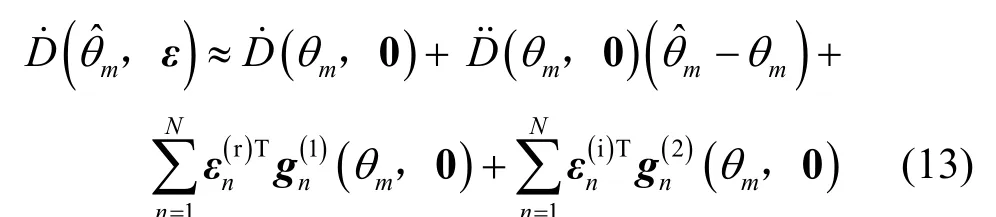
其中，D˙（θ ，ε） =∂ D˙ （θ，ε）∂θ，而分别表示 D˙ （θ ，ε）关于 ε（r）和 ε（i）的梯度向量。根据式nn(13)可得方位估计偏差为

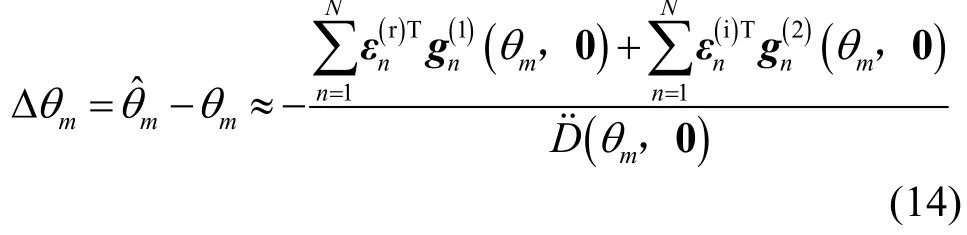
式中

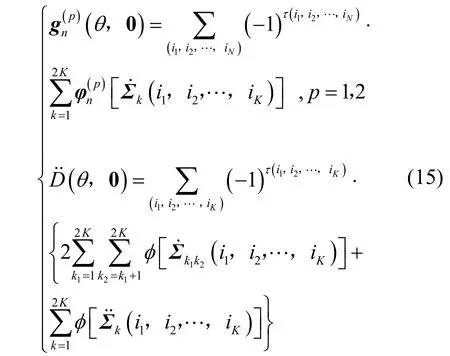
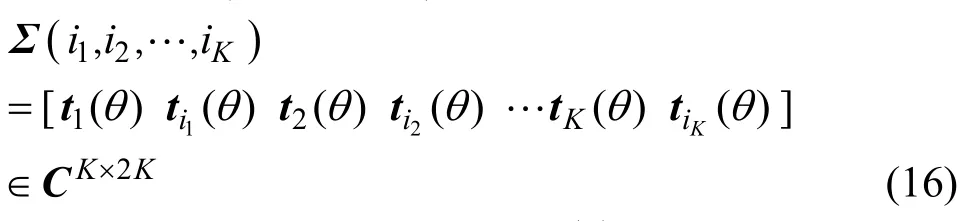
此外，式(15)中的φ[⋅]和φn(p)[⋅]（p=1，2 ）分别满足下式的标量和向量函数：

式中 f （⋅，⋅）和fn(p)（⋅，⋅）的表达式见命题2。

为了简化式(14)中的表示形式，在附录D中将

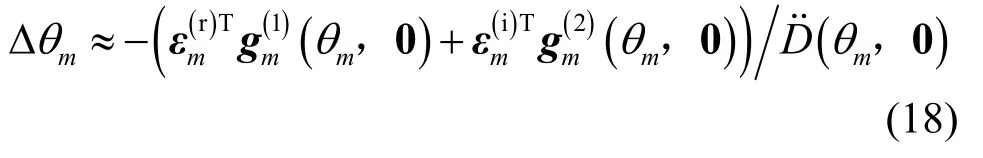
上式的物理意义在于：在仅考虑误差向量ε一阶项的条件下，第m个信源的方位估计偏差仅由对应于第m个信源阵列流型上的误差向量εm造成，而与其他误差向量 εn（n ≠m）无关。定义方位估计偏差向量 Δ θ=［Δθ1Δθ2…ΔθN］T，则由式(18)可得

5 秩减估计器的测向成功概率

本节将推导RARE的测向成功概率，为了便于分析，仍假设未预期模型误差服从高斯分布。笔者曾在文献[17]中分析了MUSIC算法的测向成功概率，这里将基于此方法推导RARE的测向成功概率。

5.1 针对单个信源的测向成功概率

首先讨论针对单个信源的测向成功概率。

定义 1[17]对于第n个信源，若满足条件，则认为是测向成功。

上述定义中的Δθ表示角度误差容限，根据式(18)可知，在高斯误差模型假设条件下，Δθn是一个服从高斯分布的随机变量，于是不难证明针对第n个信源的测向成功概率为

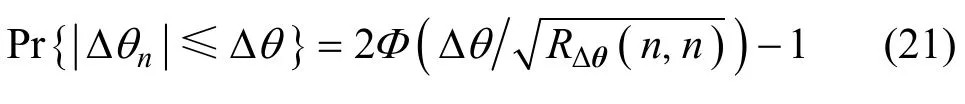
其中， RΔθ（n, n ）表示矩阵RΔθ的第n个对角元素，而其数值可通过查表获得。

5.2 两类整体测向成功概率

接着讨论两类整体测向成功概率。

定义2[17]若满足条件则认为是第一类整体测向成功。

根据式(18)可知，若εn与εm统计独立，则Δθn与Δθm也统计独立，此时第一类整体测向成功概率为

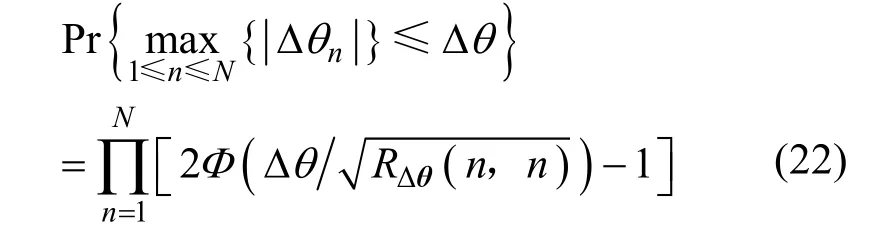
若εn与εm并不统计独立，此时第一类整体测向成功概率为

定义3[17]若满足条件，则认为是第二类整体测向成功。

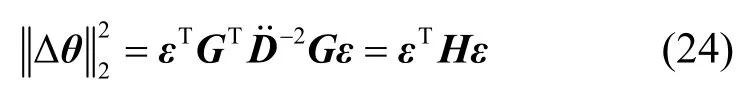
其中， H= GTD˙-2G。式(24)实质上是将表示成了高斯向量的二次型，为了计算的分布函数，可利用文献[18]中给出的一个关于随机变量分布函数和特征函数关系的公式：

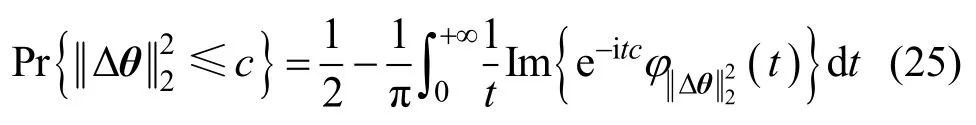
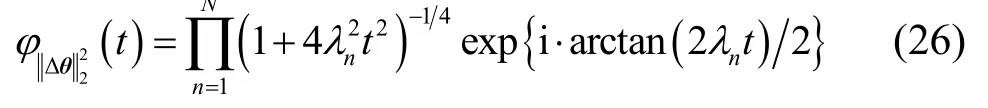
式中，λn是矩阵的正特征值。将式(26)代入式(25)可得

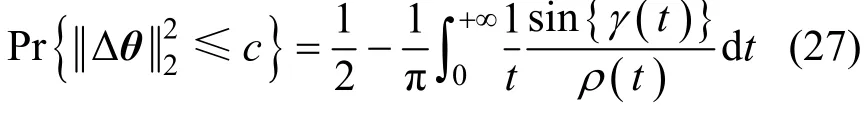
至此，本节已经给出了针对单个信源的测向成功概率和两类整体测向成功概率的计算方法，而根据文献[17]中的讨论可知：①第一类整体测向成功概率一定不大于单个信源的测向成功概率；②第一类整体测向成功概率必然小于第二类整体测向成功概率，这些结论由它们的定义方式所决定。

6 数值实验

在给出数值实验结果前，这里先给出以下几点说明：①下文都是针对文献[5,6]中提出的互耦自校正RARE所给出的数值实验；②由于本文并未考虑有限采样的影响，因此文中的协方差矩阵直接由式(8)产生；③这里假设未预期模型误差服从复圆高斯分布，即满足 E [εnεmH] =δnmσε2IM和E[εnεmT]=O；④尽管MUSIC算法也是一种特殊的RARE，但在下文的数值实验中还是分别给出了 RARE和MUSIC算法的性能曲线，其中RARE考虑了相邻3个阵元之间产生的互耦效应，即文中的 K= 3，其互耦因子分别为1、0.2+0.24i和-0.1-0.1i，而MUSIC算法则认为没有互耦效应，即文中的 K=1；⑤若不做其他说明，仿真图中分别给出了未预期模型误差的扰动方差为-35dB和-30dB 2种情况下的性能曲线；⑥计算测向成功概率的误差容限Δθ设为0.5º；⑦文中的所有实验值是进行了2 000次Monte Carlo独立实验的结果。

6.1 针对仅存在单个信源的仿真实验

假设阵列流型为8元均匀线阵，相邻2个阵元间距与波长比为0.5，现仅有一个信源到达该阵列。图1和图2分别给出了RARE和MUSIC算法的方位估计均方根误差和测向成功概率随着信源方位(与线阵夹角)的变化曲线。

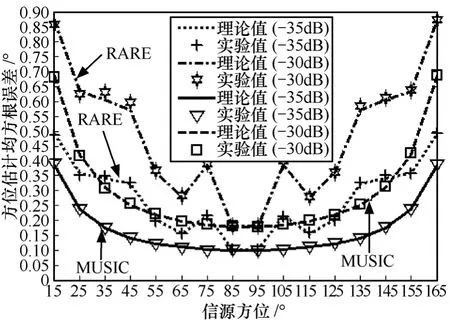
图1 方位估计均方根误差随着信源方位的变化曲线

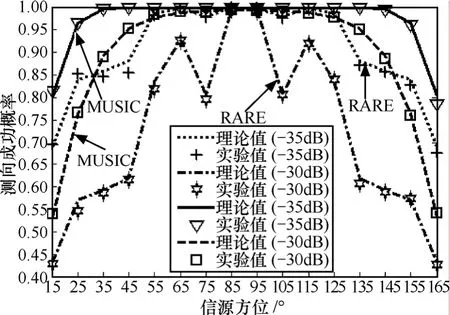
图2 测向成功概率随着信源方位的变化曲线

假设阵列流型为8元均匀圆阵，现仅有一个信源到达该阵列。固定半径与波长比为1，图3和图4分别给出了RARE和MUSIC算法的方位估计均方根误差和测向成功概率随着信源方位的变化曲线。其余仿真条件基本不变，但固定信源方位为80º，图5和图6分别给出了RARE和MUSIC算法方位估计均方根误差和测向成功概率随着半径与波长比的变化曲线。

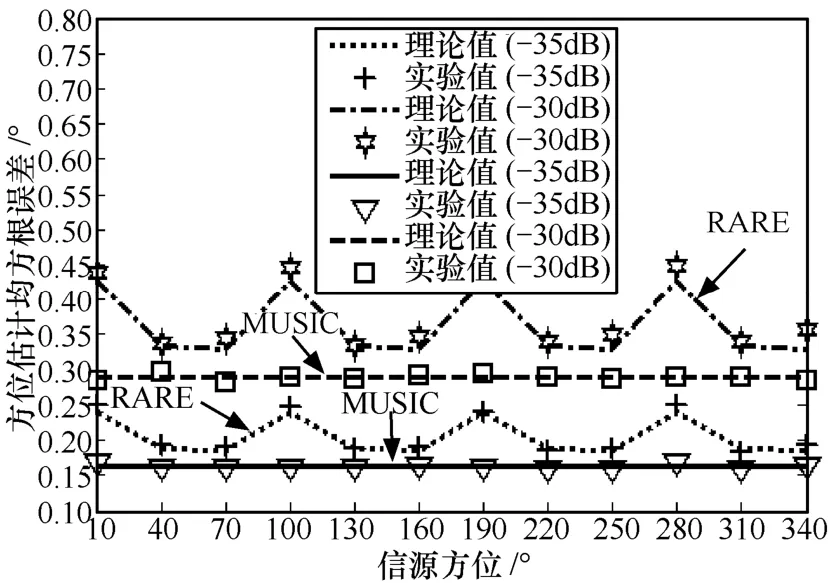
图3 方位估计均方根误差随着信源方位的变化曲线

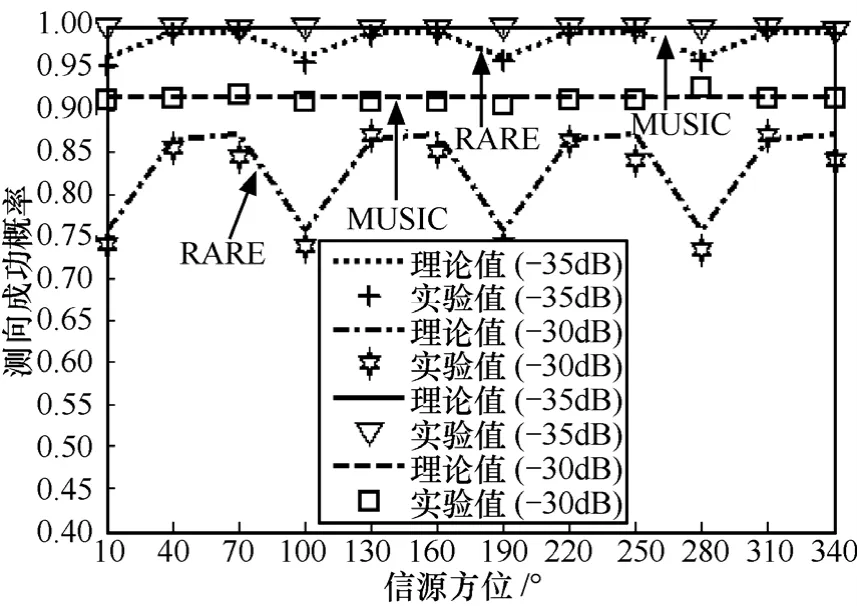
图4 测向成功概率随着信源方位的变化曲线

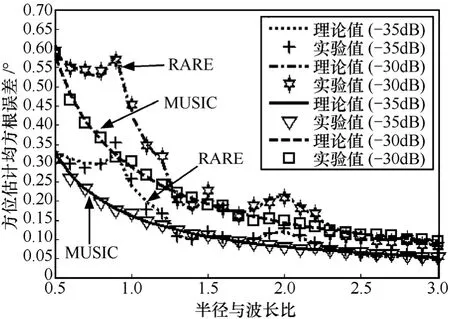
图5 方位估计均方根误差随着半径与波长比的变化曲线

图6 测向成功概率随着半径与波长比的变化曲线

从图 1～图 6中可以得到如下结论：①在上述数值实验条件下，方位估计均方根误差和测向成功概率的理论值和实验值都能够较好地吻合，从而验证了文中理论推导的正确性；②无论MUSIC算法还是 RARE，它们的方位估计精度都随着未预期模型误差的增大而降低，这一结论显然符合实际情况；③在相同条件下，MUSIC算法的方位估计精度基本优于 RARE；④对于MUSIC算法而言，当阵列是均匀线阵时，越接近法线方向信源的方位估计精度越高，而当阵列是均匀圆阵时，方位估计精度与信源方位无关，但对于RARE而言，上述性质则在局部范围内发生一定变化，这与它们各自空域谱的特性有关；⑤对于MUSIC算法而言，其方位估计精度随着半径与波长比的增大而提高，但对于 RARE而言，尽管其方位估计精度总体上也随着半径与波长比的增大而提高，但在局部范围内，上述性质也发生了一定变化，这同样与它们各自空域谱的特性有关。

6.2 针对存在2个信源的仿真实验

当存在2个信源时，由于篇幅有限，这里仅针对均匀圆阵给出数值实验。假设阵列流型为 9元均匀圆阵，半径与波长比为 1，现有 2个等功率信源到达该阵列，其中第1个信源方位固定为45º。图7和图8分别给出了RARE和MUSIC算法的方位估计均方根误差随着信源方位间隔的变化曲线；图9和图10分别给出了RARE和MUSIC算法的单信源测向成功概率随着信源方位间隔的变化曲线；图 11和图 12分别给出了 RARE和MUSIC算法的2类整体测向成功概率随着信源方位间隔的变化曲线。

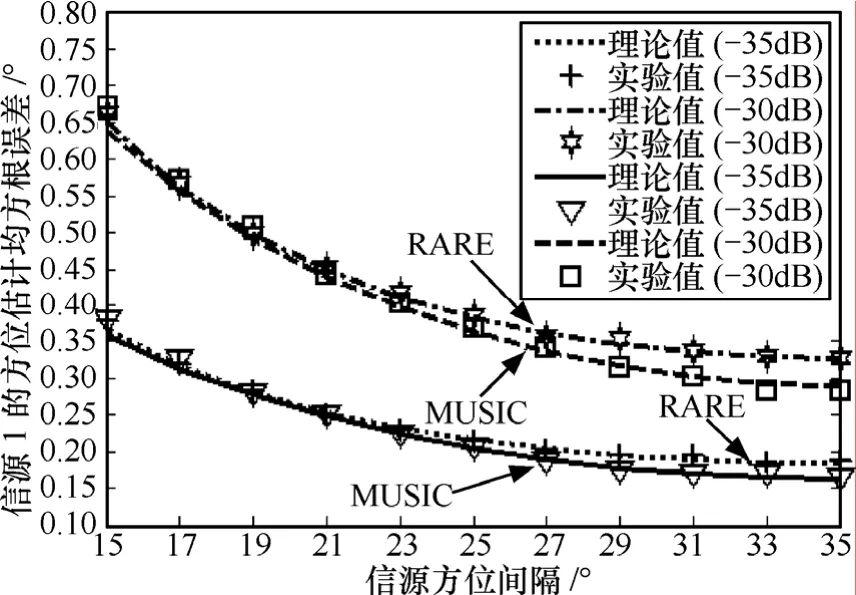
图7 信源1的方位估计均方根误差随着方位间隔的变化曲线

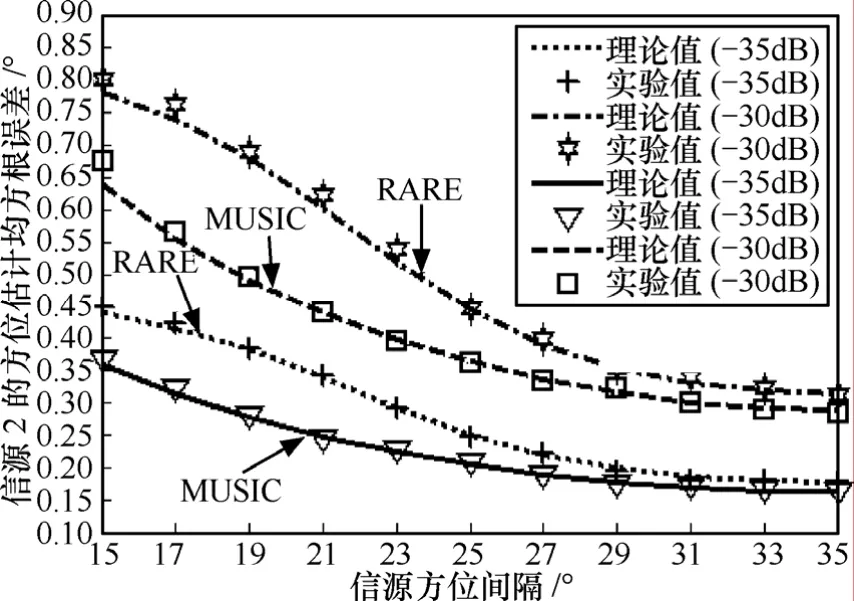
图8 信源2的方位估计均方根误差随着方位间隔的变化曲线

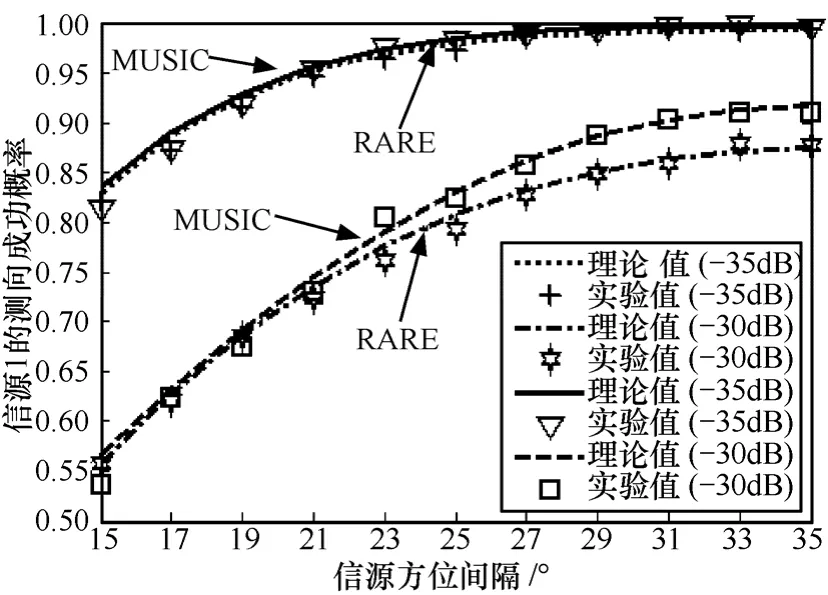
图9 信源1的测向成功概率随着方位间隔的变化曲线

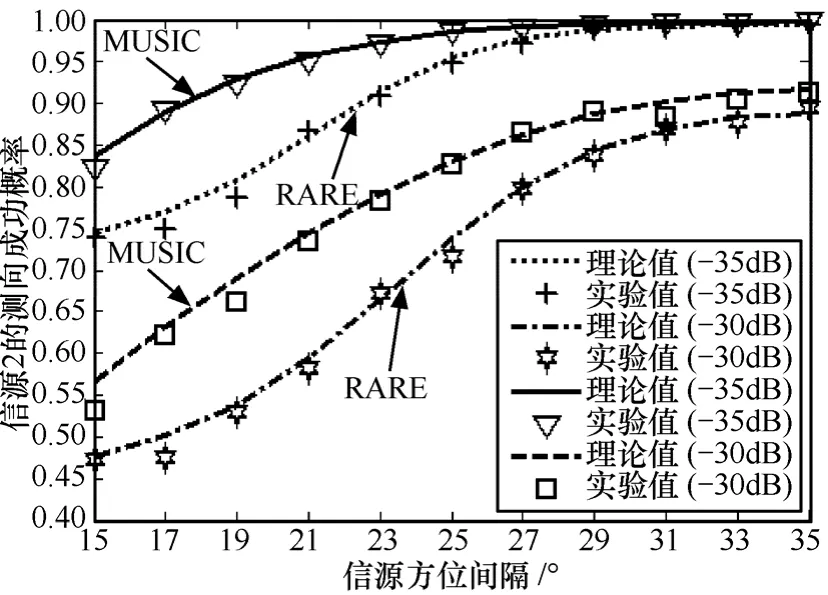
图10 信源2的测向成功概率随着方位间隔的变化曲线

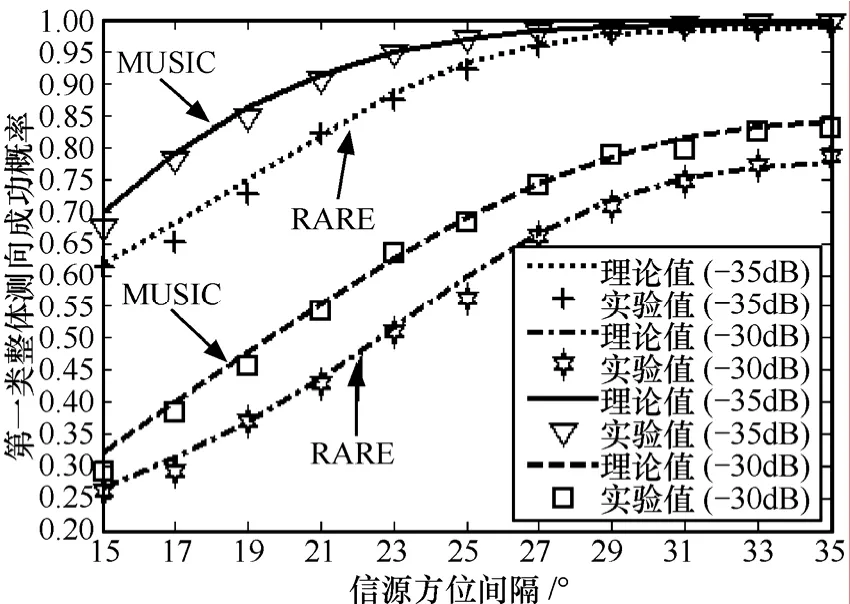
图11 第1类整体测向成功概率随着方位间隔的变化曲线

从图7～图12中可以得到如下结论：①在上述数值实验条件下，理论值和实验值仍然能够较好地吻合，从而进一步验证了文中理论推导的正确性；②无论MUSIC算法还是RARE，它们的方位估计精度仍都随着未预期模型误差的增大而降低；③在相同条件下，MUSIC算法的方位估计精度仍要基本优于RARE；④对于均匀圆阵而言，无论是MUSIC算法还是RARE，它们的方位估计精度都会随着信源方位间隔的增大而提高，并且对于MUSIC算法而言，2个信源虽然方位不同，但是方位估计精度几乎一致，但对于RARE而言，2个信源的方位估计精度则存在一定差异，这与第6.1节中所给出的结论④相似；⑤第一类整体测向成功概率始终不会高于单个信源的测向成功概率，并且第一类整体测向成功概率始终小于第二类整体测向成功概率，这一结论符合它们的定义方式。

最后，这里通过仿真实验验证式(18)所呈现的一个性质，即在仅考虑误差向量ε一阶项的条件下，第m个信源的方位估计偏差仅由对应于第m个信源阵列流型上的误差向量εm造成，而与其他误差向量εn（n ≠m）无关。仿真条件基本同上，但是固定2个信源的方位为45º和65º。图13给出了在固定信源1阵列流型扰动方差为-35dB的条件下，RARE和 MUSIC算法的方位估计均方根误差随着信源 2阵列流型扰动方差的变化曲线；图 14给出了在固定信源 2阵列流型扰动方差为-35dB的条件下，RARE和MUSIC算法的方位估计均方根误差随着信源1阵列流型扰动方差的变化曲线。

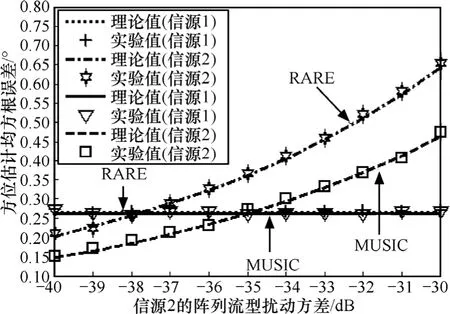
图13 方位估计均方根误差随着信源2的阵列流型扰动方差的变化曲线

从图13和图14中可以看出，当信源2的阵列流型扰动方差增大时，信源2的方位估计误差会增大，但是信源1的方位估计精度基本保持不变，类似地，当信源1的阵列流型扰动方差增大时，信源1的方位估计误差会增大，但是信源2的方位估计精度基本保持不变，从而验证了式(18)所呈现出的性质，这也进一步验证了文中理论推导的有效性。但需要指出的是，上述性质仅在一阶误差分析的条件下成立，即模型误差足够小以至于它的二阶项可以忽略。

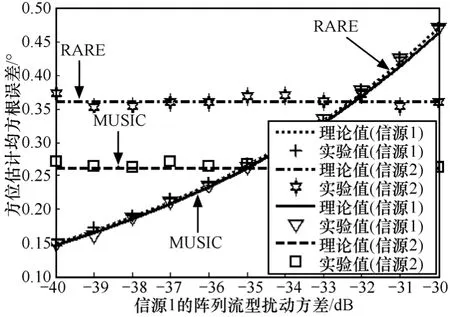
图14 方位估计均方根误差随着信源1的阵列流型扰动方差的变化曲线

7 结束语

本文从理论上定量分析了未预期模型误差影响下RARE的方位估计性能，分别推导了RARE的方位估计均方误差和测向成功概率，并依据文献[5～6]中所提出的针对均匀阵列互耦自校正 RARE给出了数值实验。仿真结果表明理论值和仿真实验值能够较好地吻合，从而验证了理论推导的有效性。文中的结论对于RARE的工程应用具有一定指导意义。需要指出的是，由于文中的推导忽略了模型误差的高阶项，因此在大模型误差情况下的性能分析仍需要进一步研究。

附录A 命题1的证明

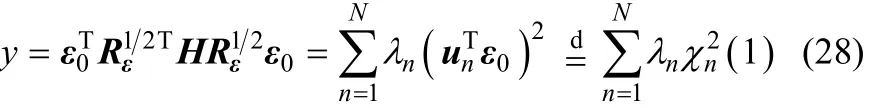
式中“=d”表示等式两边的随机变量服从相同的概率分布，un是对应于λn的单位特征向量，并且各个特征向量之间相互正交。当n≠m时，式(28)中的χn2（1）与χm2（1）统计独立，这是因为而对于 2个零均值的高斯随机变量而言，正交则意味着统计独立。根据引理1可知，再根据相互独立的随机变量和的特征函数等于各自特征函数乘积这一性质可知命题1成立。

附录B 命题2的证明

式(2)是关于E中元素一阶Taylor级数展开的形式，所以仅需要证明式(3)成立即可。记向量 εn（r）和εn（i）中的第m个元素分别为 εm（rn）和εm（in），则有

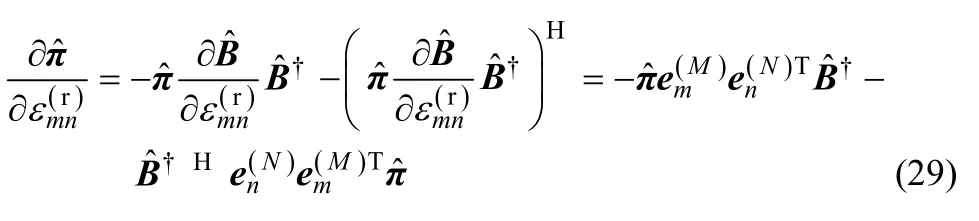
进一步可得

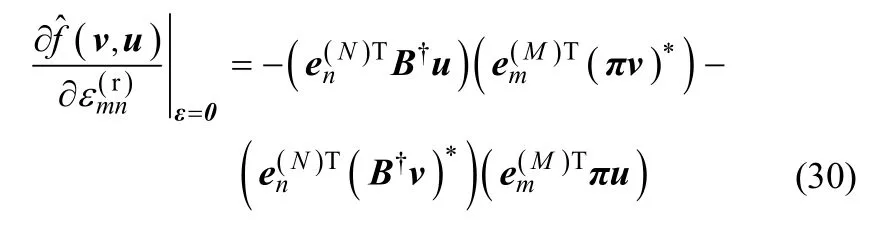
于是有

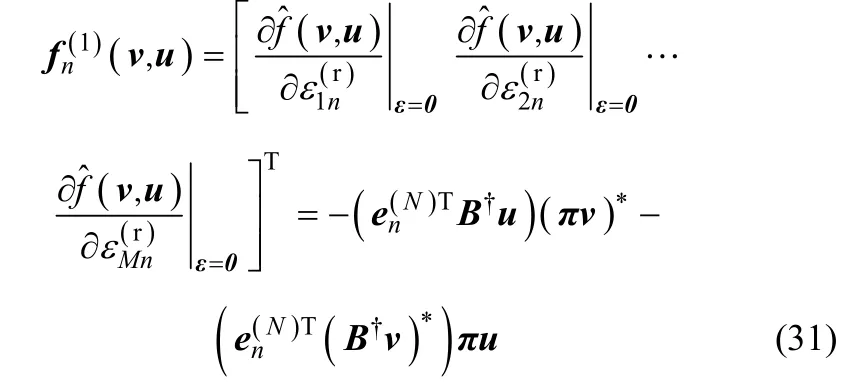
同理可证关于 fn（2）（v，u）的等式成立。

附录C 推理1的证明

采用数学归纳法进行证明，当 K =2时

假设当K=L时等式成立，则当 K=L+ 1时根据假设可得

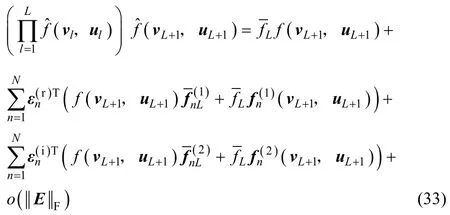
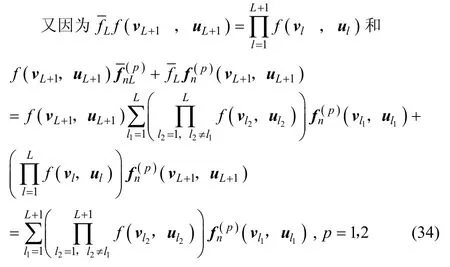
将上面两式代入式(33)中可得当 K=L+ 1时等式成立，于是推论1成立。

为了简化问题的讨论，这里仅对 K =2的情况进行证明，但其证明方法可推广至 K ＞2的情况．当 K = 2 时，可将预期阵列流型向量表示为

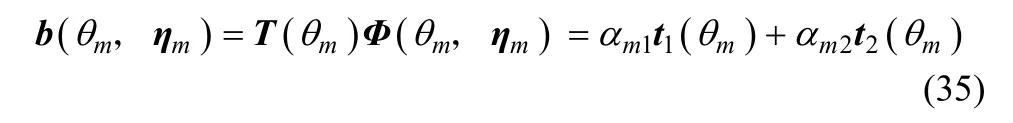
于是根据正交投影矩阵的性质可得 αm1π t1（θm）+αm2π t2（θm）=0，进一步可知 π t2（ θm）= βmπt1（ θm），其中，βm=-αm1αm2。再根据等式 B†B= IN可知：

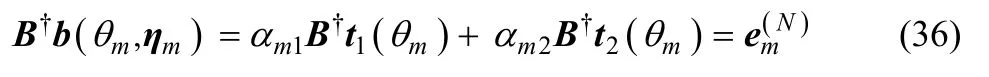
于是当n≠m时可得

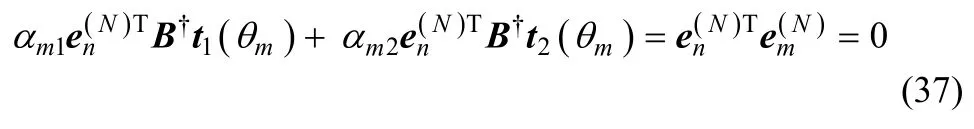
进一步可知

根据式(15)可知

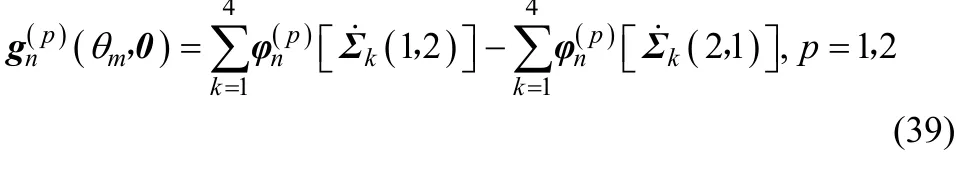
当n≠m时，根据式(17)和式(38)可分别推得

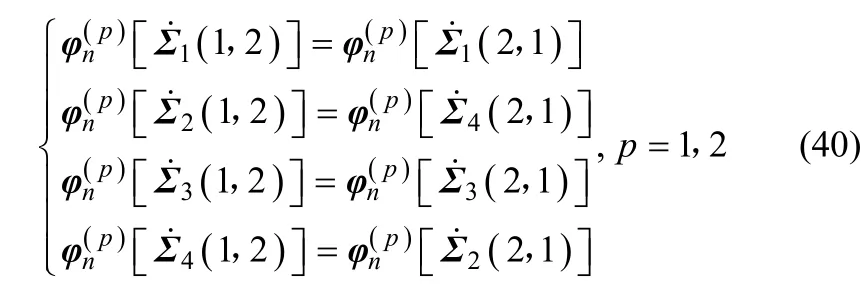
[1] SEE C M S. Sensor array calibration in the presence of mutual coupling and unknown sensor gains and phases[J]. Electronics Letters,1994, 30(5): 373-374.

[2] 贾永康, 保铮, 吴洹. 一种阵列天线阵元位置、幅度及相位误差的有源校正方法[J]. 电子学报, 1996, 24(3): 47-52.JIA Y K, BAO Z, WU H. A new calibration technique with signal sources for position, gain and phase uncertainty of sensor array[J].Acta Electronica Sinica, 1996, 24(3): 47-52.

[3] SELLONE F, SERRA A. A novel mutual coupling compensation algorithm for uniform and linear arrays[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 560-573.

[4] WIJNHOLDS S J, VEEN A J. Multisource self-calibration for sensor arrays[J]. IEEE Transactions on Signal Processing, 2009, 57(9):3512-3522.

[5] 王布宏, 王永良, 陈辉. 均匀线阵互耦条件下的鲁棒 DOA 估计及互耦自校正[J]. 中国科学E辑: 技术科学, 2004, 34(2): 229-235.WANG B H, WANG Y L, CHEN H. Robust DOA estimation and mutual coupling self-calibration algorithm for uniform linear array[J]. Science in China Series E: Technological Sciences, 2004, 34(2): 229-235.

[6] QI C, WANG Y, ZHANG Y, CHEN H. DOA estimation and selfcalibration algorithm for uniform circular array[J]. Electronics Letters,2005, 41(20): 1092-1094.

[7] XIANG L, YE Z, XU X, et al. Direction of arrival estimation for uniform circular array based on fourth-order cumulants in the presence of unknown mutual coupling[J]. IET Microwaves, Antennas and Propagation, 2008, 2(3): 281-287.

[8] GOOSSENS R, ROGIER H. A hybrid UCA-RARE/Root-MUSIC approach for 2-D direction of arrival estimation in uniform circular arrays in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(3): 841-849.

[9] WANG B H, HUI H T. Decoupled 2-D direction of arrival estimation using compact uniform circular arrays in the presence of elevation-dependent mutual coupling[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(3): 747-755.

[10] 王布宏, 王永良, 陈辉等. 方位依赖阵元幅相误差校正的辅助阵元法[J]. 中国科学E辑: 信息科学, 2004, 34(8): 906-918.WANG B H, WANG Y L, CHEN H, et al. Array calibration of angularly dependent gain and phase uncertainties with carry-on instrumental sensors[J]. Science in China Series E: Information Sciences, 2004,34(8): 906-918.

[11] PESAVENTO M, GERSHMAN A B, WONG K M. Direction finding in partly calibrated sensor arrays composed of multiple subarrays[J]. IEEE Transactions on Signal Processing, 2002, 50(9):2103-2115.

[12] SEE C M S, GERSHMAN A B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 329-338.

[13] 吴彪, 陈辉, 李建东. 均匀线阵互耦矩阵非Toeplitz条件下的DOA估计[J]. 雷达科学与技术, 2009, 7(5): 358-364.WU B, CHEN H, LI J D. Direction of arrival(DOA) estimation under non-toeplitz mutual coupling matrix of ULA[J]. Radar Science and Technology, 2009, 7(5): 358-364.

[14] BELLONI F, KOIVUNEN V. Beamspace transform for UCA: error analysis and bias reduction[J]. IEEE Transactions on Signal Processing,2006, 54(8): 3078-3089.

[15] SHERIF A E, ALEX B G, KON M W. Rank reduction direction-ofarrival estimators with an improved robustness against subarray orientation errors[J]. IEEE Transactions on Signal Processing, 2006, 54(5):1951-1955.

[16] 张润楚. 多元统计分析[M]. 北京: 科学出版社, 2006. 32-33.ZHANG R C. Multivariate Statistical Analysis[M]. Beijing: Publishing House of Science, 2006. 32-33.

[17] 王鼎, 吴瑛. 模型误差条件下 MUSIC算法的测向成功概率[J]. 应用科学学报, 2010, 28(3): 289-296.WANG D, WU Y. Success probability of direction-finding of MUSIC algorithm with modeling errors[J]. Journal of Applied Sciences, 2010,28(3): 289-296.

[18] DUGINA T N, MARTYNOV G V. Computing the distribution function of the ratio of quadratic forms in normal variables[J]. Journal of Mathematical Sciences, 1991, 53(6): 628-631.